Vector Calculus for Engineers from Coursera

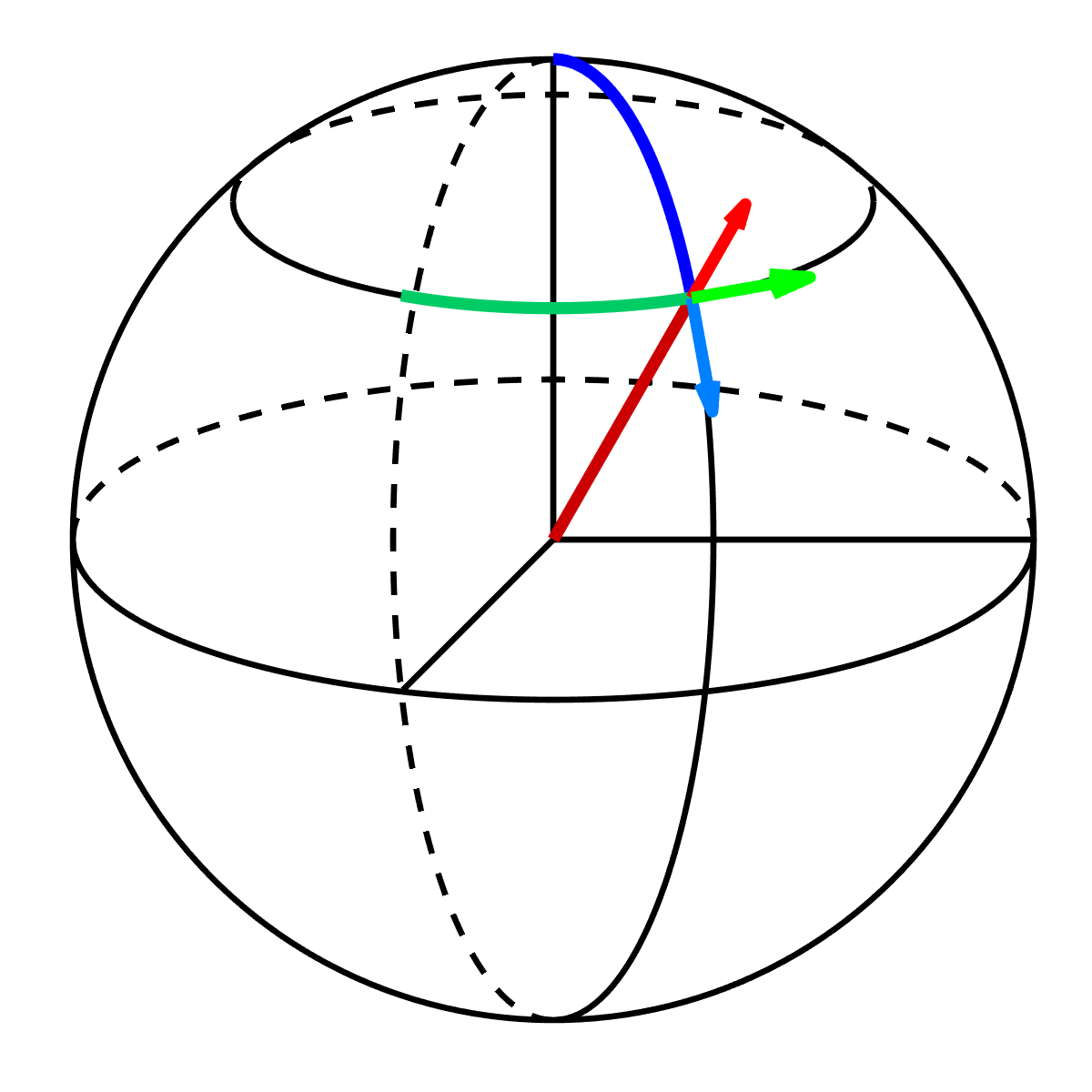
This course covers both the theoretical foundations and practical applications of Vector Calculus. During the first week, students will learn about scalar and vector fields. In the second week, they will differentiate fields. The third week focuses on multidimensional integration and curvilinear coordinate systems. Line and surface integrals are covered in the fourth week, while the fifth week explores the fundamental theorems of vector calculus, including the gradient theorem, the divergence theorem, and Stokes' theorem. These theorems are essential for subjects in engineering such as Electromagnetism and Fluid Mechanics.

Note that this course may also be referred to as Multivariable or Multivariate Calculus or Calculus 3 at some universities. A prerequisite for this course is two semesters of single variable calculus (differentiation and integration).

The course includes 53 concise lecture videos, each followed by a few problems to solve. After each major topic, there is a short practice quiz. At the end of each week, there is an assessed quiz. Solutions to the problems and practice quizzes can be found in the instructor-provided lecture notes.

Download the lecture notes from the link

https://www.math.hkust.edu.hk/~machas/vector-calculus-for-engineers.pdf

Watch the promotional video from the link

https://youtu.be/qUseabHb6Vk

What's inside

Syllabus

Vectors

Vectors are mathematical constructs that have both length and direction. We define vectors and show how to add and subtract them, and how to multiply them using the dot and cross products. We apply vectors to study the analytical geometry of lines and planes, and define the Kronecker delta and the Levi-Civita symbol to prove vector identities. Finally, we define the important concepts of scalar and vector fields.

Differentiation

Scalar and vector fields can be differentiated. We define the partial derivative and derive the method of least squares as a minimization problem. We learn how to use the chain rule for a function of several variables, and derive the triple product rule used in chemical engineering. We define the gradient, divergence, curl, and Laplacian. We learn some useful vector calculus identities and derive them using the Kronecker delta and Levi-Civita symbol. We use vector identities to derive the electromagnetic wave equation from Maxwell's equation in free space. Electromagnetic waves form the basis of all modern communication technologies.

Integration and Curvilinear Coordinates

Integration can be extended to functions of several variables. We learn how to perform double and triple integrals. We define curvilinear coordinates, namely polar coordinates in two dimensions, and cylindrical and spherical coordinates in three dimensions, and use them to simplify problems with circular, cylindrical or spherical symmetry. We learn how to write differential operators in curvilinear coordinates and how to change variables in multidimensional integrals using the Jacobian of the transformation.

Line and Surface Integrals

Scalar or vector fields can be integrated over curves or surfaces. We learn how to take the line integral of a scalar field and use the line integral to compute arc lengths. We then learn how to take line integrals of vector fields by taking the dot product of the vector field with tangent unit vectors to the curve. Consideration of the line integral of a force field results in the work-energy theorem. Next, we learn how to take the surface integral of a scalar field and use the surface integral to compute surface areas. We then learn how to take the surface integral of a vector field by taking the dot product of the vector field with the normal unit vector to the surface. The surface integral of a velocity field is used to define the mass flux of a fluid through a surface.

Fundamental Theorems

The fundamental theorem of calculus links integration with differentiation. Here, we learn the related fundamental theorems of vector calculus. These include the gradient theorem, the divergence theorem, and Stokes' theorem. We show how these theorems are used to derive continuity equations and the law of conservation of energy. We show how to define the divergence and curl in coordinate-free form, and convert the integral version of Maxwell's equations into differential form.

Good to know

Know what's good

, what to watch for

, and possible dealbreakers

Emphasizes Vector Calculus's applications in engineering, particularly Electromagnetism and Fluid Mechanics

Provides a comprehensive overview of vector calculus, from basic concepts to advanced theorems

Taught by Jeffrey R. Chasnov, an experienced instructor in mathematics

Includes practice quizzes and assessed quizzes to reinforce learning

Requires prerequisite knowledge of single variable calculus (differentiation and integration)

Covers core concepts of vector calculus, including vector identities and multidimensional integration

Reviews summary

Wellrounded vector calculus

learners say this extremely good, challenging, and wellrounded course covers a broad range of topics in vector calculus with a focus on practical applications for engineers. The videos are clear and the practice quizzes and notes are helpful, allowing learners to understand the material well. However, the time commitment is significant and some learners may find it difficult to keep up, especially in the later weeks.

The course is challenging, but learners who are prepared can succeed.

"Difficult but excellent course."

"The course has helped me understand and apply my knowledge of Vector Calculus."

"It was a very educating course on various theorems, proof of laws, various subtopics on integration and differentiation."

Professor Chasnov is knowledgeable and engaging.

"The course was very well taught but steep gradient and in some cases the work booklet skips over intermediate steps when deriving the answers."

"Excellent course! It was challenging at times, but the pacing was excellent."

"It was an awesome experience, and learning all about the practical application of vectors has broadened my mind. Great videos! Easy t understand."

Challenging but rewarding quizzes and assignments help solidify learning.

"The quizzes and the practice quizzes were a bit challenging."

"Great overview of Vector Calculus, I have confidence to tutor my son on this subject now."

"Very good, i liked this course a lot."

Excellent course material with applications to real-world engineering problems.

"Excellent course. Covers all the basic vector calculus an engineer needs to know."

"Very good course. Covers all the basic vector calculus an engineer needs to know."

"I highly recommend this course to other students who're interested in this subject."

Intensive course requiring a significant time commitment each week.

"I feel like more examples should be used will explaining"

"Good videos and derivations."

"It's sufficient for easily understand vector calculus and well explained."

Activities

Be better prepared before your course. Deepen your understanding during and after it. Supplement your coursework and achieve mastery of the topics covered in Vector Calculus for Engineers with these activities:

Watch MIT OpenCourseWare Lectures on Vector Calculus

Show steps

Supplement your understanding of Vector Calculus with clear and concise video lectures.

Show steps

Go to the MIT OpenCourseWare website and search for 'Vector Calculus'.
Watch the video lectures in order.
Take notes during the lectures.
Complete the practice problems at the end of each lecture.

Solve Vector Calculus Problems

Show steps

Strengthen your problem-solving skills by practicing various Vector Calculus problems.

Show steps

Find practice problems in your textbook or online.
Start solving the problems.
Check your answers against the provided solutions.
Review the problems you got wrong.

Develop a Vector Calculus Cheat Sheet

Show steps

Create a quick reference guide for the key concepts and formulas in Vector Calculus.

Show steps

Identify the main topics and formulas in Vector Calculus.
Write down the information in a clear and concise way.
Organize the information into a logical order.
Review your cheat sheet regularly.

Two other activities

Expand to see all activities and additional details

Show all five activities

Read 'Vector Calculus' by Jerrold Marsden and Anthony Tromba

Show steps

Deepen your understanding of Vector Calculus by reading a comprehensive and authoritative textbook.

Show steps

Purchase or borrow the book.
Read the book in order.
Take notes during your reading.
Complete the practice problems at the end of each chapter.

Participate in a Vector Calculus Competition

Show steps

Test your skills and knowledge of Vector Calculus against other students in a competitive setting.

Show steps

Find a Vector Calculus competition.
Register for the competition.
Prepare for the competition by studying and practicing.
Take the competition.

Career center

Learners who complete Vector Calculus for Engineers will develop knowledge and skills that may be useful to these careers:

Data Scientist

Data Scientists collect, analyze, and interpret data to help businesses make informed decisions. Vector calculus is essential for this role, as it helps data scientists understand the structure and relationships in data, and how these relationships can be used to make predictions. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex data structures and relationships that are used in data science.

See salaries and explore the career path for Data Scientist

Operations Research Analyst

Operations Research Analysts use mathematical models to help businesses make better decisions. Vector calculus is essential for this role, as it helps analysts understand the relationships between different variables, and how these relationships can be used to optimize business processes. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex mathematical models that are used in operations research.

See salaries and explore the career path for Operations Research Analyst

Statistician

Statisticians collect, analyze, and interpret data to help businesses and organizations make informed decisions. Vector calculus is essential for this role, as it helps statisticians understand the structure and relationships in data, and how these relationships can be used to make inferences about the population from which the data was collected. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex statistical models that are used in statistics.

See salaries and explore the career path for Statistician

Financial Analyst

Financial Analysts evaluate the financial performance of companies and make recommendations on investment strategies. Vector calculus is essential for this role, as it helps analysts understand the relationships between different financial variables, and how these relationships can be used to make informed investment decisions. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex financial models that are used in financial analysis.

See salaries and explore the career path for Financial Analyst

Actuary

Actuaries use mathematical models to assess risk and uncertainty. Vector calculus is essential for this role, as it helps actuaries understand the relationships between different risk factors, and how these relationships can be used to calculate insurance premiums and other financial products. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex mathematical models that are used in actuarial science.

See salaries and explore the career path for Actuary

Computer Scientist

Computer Scientists design, develop, and implement computer software and systems. Vector calculus is essential for this role, as it helps computer scientists understand the mathematical foundations of computer graphics, computer vision, and robotics. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex mathematical models that are used in computer science.

See salaries and explore the career path for Computer Scientist

Mechanical Engineer

Mechanical Engineers design, build, and maintain machines and mechanical systems. Vector calculus is essential for this role, as it helps engineers understand the forces and stresses acting on machines, and how these forces affect their performance. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex forces that act on mechanical systems.

See salaries and explore the career path for Mechanical Engineer

Materials Scientist

Materials Scientists research and develop new materials, such as metals, ceramics, and polymers. Vector calculus is essential for this role, as it helps scientists understand the structure and properties of materials, and how these properties affect their performance. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex structure and properties of materials.

See salaries and explore the career path for Materials Scientist

Chemical Engineer

Chemical Engineers design, build, and operate chemical plants and processes. Vector calculus is essential for this role, as it helps engineers understand the flow of fluids and the transfer of heat and mass. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex flows and processes that occur in chemical plants.

See salaries and explore the career path for Chemical Engineer

Civil Engineer

Civil Engineers design, build, and maintain infrastructure, such as bridges, roads, and buildings. Vector calculus is essential for this role, as it helps engineers understand the forces acting on structures, and how these forces affect their stability. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex forces that act on civil engineering structures.

See salaries and explore the career path for Civil Engineer

Aerospace Engineer

Aerospace Engineers design, test, and oversee the production of aircraft, spacecraft, and their components. Vector calculus is essential for this role, as it helps engineers understand the forces acting on aircraft and spacecraft, and how these forces affect their performance. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex forces that act on aerospace vehicles.

See salaries and explore the career path for Aerospace Engineer

Electrical Engineer

Electrical Engineers design, build, and maintain electrical systems, such as power plants, transmission lines, and electronic devices. Vector calculus is essential for this role, as it helps engineers understand the flow of electricity and the electromagnetic fields that surround electrical devices. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex flows and fields that occur in electrical systems.

See salaries and explore the career path for Electrical Engineer

Astronomer

Astronomers study the stars, planets, and other objects in the universe. Vector calculus is essential for this role, as it helps astronomers understand the motion of celestial objects, and how this motion is affected by the forces of gravity and other forces. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex motions of celestial objects.

See salaries and explore the career path for Astronomer

Physicist

Physicists study the fundamental laws of nature. Vector calculus is essential for this role, as it helps physicists understand the forces and interactions between objects, and how these forces and interactions affect the motion of objects. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex laws of physics.

See salaries and explore the career path for Physicist

Geophysicist

Geophysicists study the Earth's physical properties and processes. Vector calculus is essential for this role, as it helps geophysicists understand the forces and interactions within the Earth, and how these forces and interactions affect the Earth's structure and evolution. This course provides a strong foundation in vector calculus, covering topics such as vector fields, differentiation, integration, and curvilinear coordinates. These concepts are essential for understanding the complex forces and interactions that occur within the Earth.

See salaries and explore the career path for Geophysicist