Support Vector Machines

Introduction to Support Vector Machines

Support Vector Machines (SVMs) are a powerful and versatile set of supervised machine learning algorithms used for classification, regression, and outlier detection tasks. At a high level, an SVM aims to find an optimal hyperplane that best separates data points belonging to different classes in a multi-dimensional space. This might sound complex, but the core idea is about drawing the best possible "line" (or plane, or hyperplane in higher dimensions) to distinguish between groups of data.

Working with SVMs can be quite engaging. Imagine the satisfaction of building a model that can accurately categorize text, identify objects in images, or even predict market trends. The ability of SVMs to handle high-dimensional data and find complex relationships makes them a fascinating tool in the world of artificial intelligence and data science. Furthermore, understanding the mathematical underpinnings of SVMs, such as optimization theory and kernel methods, can be a deeply rewarding intellectual pursuit.

What are Support Vector Machines?

This section delves into the fundamental aspects of SVMs, providing a clear understanding of what they are, how they evolved, and how they compare to other machine learning techniques. We will also define some key terms that are essential for grasping the mechanics of SVMs.

Definition and Core Principles of SVM

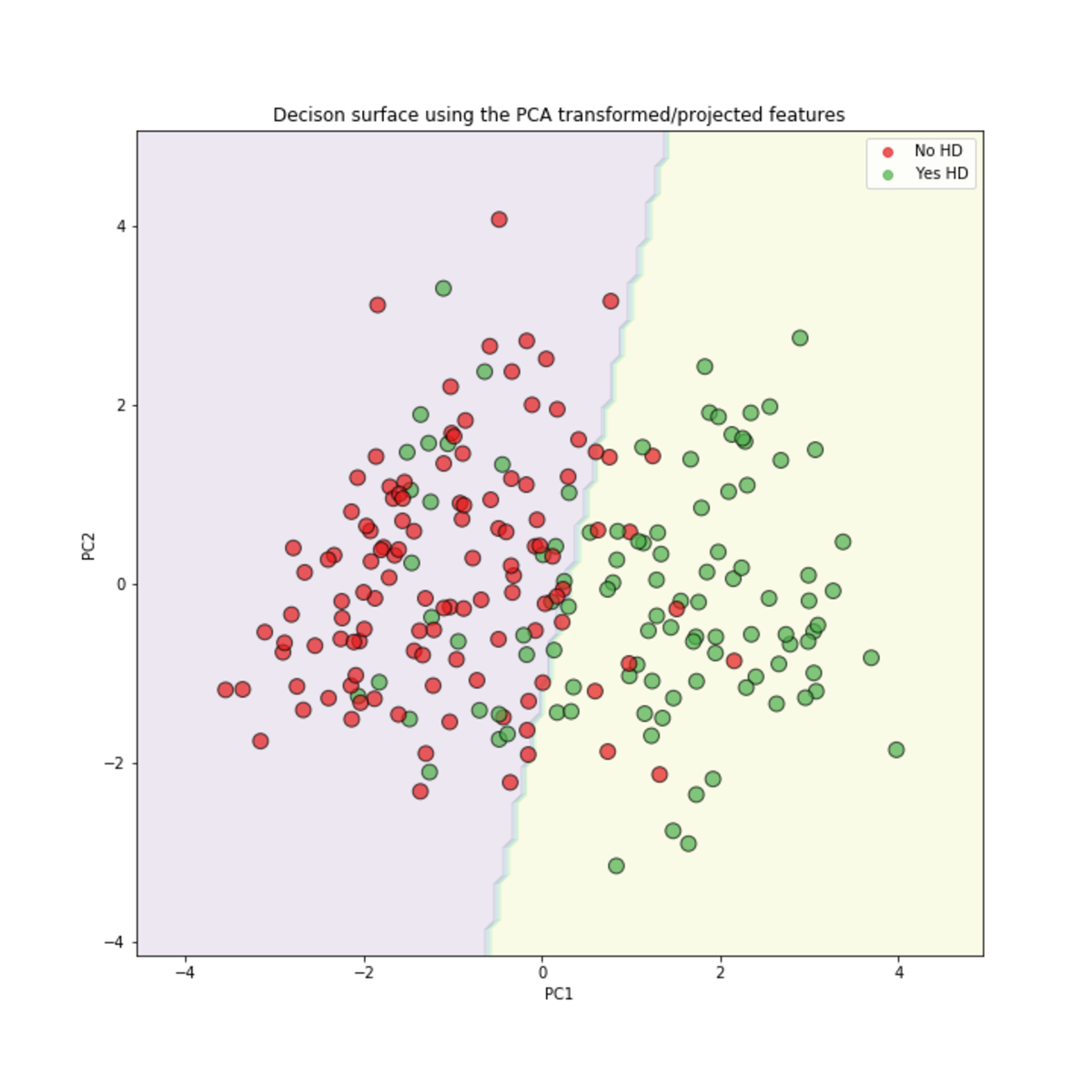
A Support Vector Machine (SVM) is a supervised machine learning algorithm primarily used for classification problems, though it can also be adapted for regression tasks (Support Vector Regression or SVR). The fundamental principle of an SVM is to find an optimal hyperplane that separates data points of different classes in a feature space. This hyperplane is chosen to maximize the margin, which is the distance between the hyperplane and the nearest data points from each class. These closest data points are called "support vectors" because they are the critical elements that "support" or define the position and orientation of the hyperplane.

The goal of an SVM is to create the widest possible "street" between classes, which helps in generalizing well to new, unseen data. For data that is not linearly separable in its original space, SVMs employ a technique called the "kernel trick." The kernel trick involves mapping the data into a higher-dimensional space where a linear separation might be possible. This allows SVMs to effectively model complex, non-linear relationships.

The core idea is that by focusing on the most critical data points (the support vectors) and maximizing the margin, SVMs can achieve robust and accurate classification. This makes them effective even in high-dimensional spaces and when the number of dimensions exceeds the number of samples.

Historical Development and Key Contributors

The foundational concepts for Support Vector Machines were developed by Vladimir N. Vapnik and Alexey Ya. Chervonenkis in the 1960s. Their work on statistical learning theory, often referred to as VC theory, laid the theoretical groundwork for SVMs. The original SVM algorithm, proposed in 1963, was a linear classifier.

A significant advancement came in 1992 when Bernhard Boser, Isabelle Guyon, and Vladimir Vapnik introduced a method to create nonlinear classifiers by applying the kernel trick to maximum-margin hyperplanes. This development dramatically increased the versatility and power of SVMs, allowing them to tackle a much wider range of complex problems. The "soft margin" version of SVM, which is commonly used today and allows for some misclassification of data points, was proposed by Corinna Cortes and Vladimir Vapnik in 1993 and published in 1995. These contributions transformed SVMs into one of the most studied and effective machine learning models.

These courses can help build a foundation in the historical context and fundamental ideas behind SVMs.

The following books delve deeper into the statistical learning theory that underpins SVMs and were authored by key figures in its development.

You may also wish to explore these topics if you're interested in the broader field:

Comparison with Other Classification Algorithms

Support Vector Machines offer distinct advantages and disadvantages when compared to other popular classification algorithms. For instance, compared to Logistic Regression, SVMs typically perform better with high-dimensional and unstructured datasets, such as image and text data. SVMs are also considered less sensitive to overfitting. However, SVMs can be more computationally expensive than logistic regression.

When contrasted with Decision Trees, SVMs tend to perform better with high-dimensional data and are generally less prone to overfitting. Decision trees, on the other hand, are often faster to train, especially with smaller datasets, and are generally easier to interpret.

Against Naive Bayes classifiers, SVMs often show better performance when the data is not linearly separable. Naive Bayes models are generally simpler and faster to train. However, SVMs might require more careful tuning of hyperparameters and can be more computationally intensive. One study comparing SVM with several other classifiers, including Random Forests and K-Nearest Neighbors, found SVM to be a highly accurate classifier, outperforming many others in specific experimental conditions. Another comparison focused on text classification noted that SVM achieved higher accuracy than a decision tree model on the 20 Newsgroups dataset.

Ultimately, the choice of algorithm depends on the specific characteristics of the dataset, the dimensionality of the data, the available computational resources, and the desired interpretability of the model.

These courses offer a broader view of classification algorithms, allowing for a comparative understanding.

Key Terminology (Hyperplanes, Margins, Support Vectors)

Understanding a few key terms is crucial for comprehending how Support Vector Machines operate.

A hyperplane is the decision boundary that an SVM aims to find. In a two-dimensional space (like a scatter plot with two features), the hyperplane is simply a line. In three dimensions, it's a plane. In spaces with more than three dimensions (which is common in machine learning), it's called a hyperplane. Essentially, it's a flat affine subspace that separates the data points into different classes. The equation of a hyperplane in a linear classification scenario is typically represented as w*x + b = 0, where 'w' is the weight vector, 'x' is the input vector, and 'b' is the bias term.

The margin is the distance between the hyperplane and the closest data points from either class. SVMs are designed to maximize this margin. A larger margin generally indicates a more robust classifier that is less likely to misclassify new, unseen data points. Think of it as creating the widest possible "street" separating the two groups of data points.

Support vectors are the data points that lie closest to the hyperplane. These are the critical data points that define the position and orientation of the hyperplane. If these support vectors were moved or removed, the hyperplane would change. Other data points, further away from the margin, do not influence the hyperplane's position. This is why SVMs are considered memory efficient, as the decision function relies only on this subset of training points.

These concepts are fundamental to understanding the mechanics and strengths of SVMs.

Mathematical Foundations of SVM

To truly master Support Vector Machines, a solid understanding of their underlying mathematical principles is essential. This section explores the key mathematical concepts that form the bedrock of SVMs, including linear algebra, optimization theory, and the ingenious "kernel trick."

Linear Algebra Concepts in SVM (Vectors, Dot Products)

Linear algebra provides the fundamental language for describing SVMs. Data points are represented as vectors in a multi-dimensional feature space. Each dimension corresponds to a feature of the data. For example, if you're classifying emails based on the frequency of certain words, each email could be a vector where each component represents the count of a specific word.

The dot product (also known as the scalar product) is a crucial operation in SVMs. Geometrically, the dot product of two vectors is related to the cosine of the angle between them and their magnitudes. In the context of SVMs, dot products are used extensively in defining the hyperplane and calculating distances. The equation of the hyperplane itself (w·x + b = 0) involves a dot product between the weight vector 'w' and the input vector 'x'. Furthermore, the kernel trick, which allows SVMs to handle non-linear data, often relies on replacing dot products in the original feature space with dot products in a higher-dimensional feature space, calculated efficiently by a kernel function.

A firm grasp of vector operations, vector spaces, and the geometric interpretation of dot products will significantly aid in understanding how SVMs delineate decision boundaries and optimize for the maximum margin.

For those looking to solidify their linear algebra foundations in the context of AI, this course may be beneficial.

Optimization Theory and Lagrange Multipliers

At its core, training an SVM is an optimization problem. The goal is to find the hyperplane (defined by the weight vector 'w' and bias 'b') that maximizes the margin between the classes, subject to the constraint that all data points are correctly classified (or, in the case of soft-margin SVMs, that misclassifications are penalized). This is typically formulated as a constrained optimization problem.

Lagrange multipliers are a mathematical technique used to solve such constrained optimization problems. Instead of directly solving for 'w' and 'b' under the classification constraints, the problem is transformed into a "dual" problem using Lagrange multipliers. This dual formulation has several advantages. It often simplifies the optimization process, and importantly, it introduces the dot products of data point vectors naturally, which is key to applying the kernel trick for non-linear classification. The solution to this dual problem provides the values of the Lagrange multipliers, and non-zero multipliers correspond to the support vectors. This elegantly highlights how only a subset of the data (the support vectors) defines the decision boundary.

Understanding optimization theory, particularly concepts like convex optimization and the method of Lagrange multipliers, is vital for a deep comprehension of how SVMs arrive at the optimal separating hyperplane.

The following book provides a comprehensive treatment of optimization in the context of SVMs and kernel methods.

Kernel Trick and Feature Space Transformation

Many real-world datasets are not linearly separable; that is, you cannot draw a straight line (or a flat hyperplane) to neatly divide the classes. This is where the kernel trick comes into play, a clever and powerful mechanism that allows SVMs to perform non-linear classification.

The core idea is to map the original input data into a higher-dimensional feature space where the data does become linearly separable (or at least more separable). Imagine you have data points in 2D that are arranged in concentric circles. You can't draw a line to separate them. However, if you map these points into 3D (e.g., by adding a third dimension based on the square of the distance from the origin), they might become separable by a plane.

The "trick" part is that SVMs don't explicitly perform this transformation and then compute dot products in this high-dimensional space, which could be computationally very expensive or even intractable if the new space is infinitely dimensional. Instead, they use kernel functions. A kernel function takes two input vectors from the original space and directly computes what their dot product would be in the higher-dimensional feature space, without ever explicitly forming the vectors in that space. This makes the computation efficient.

Common kernel functions include:

• Linear kernel: Essentially performs no transformation, used for linearly separable data.
• Polynomial kernel: Maps data to a space of polynomial features.
• Radial Basis Function (RBF) kernel (or Gaussian kernel): A very popular choice that can handle complex regions, effectively mapping data into an infinitely dimensional space.
• Sigmoid kernel: Can behave similarly to a two-layer neural network.

The choice of kernel function and its parameters is crucial for the performance of a non-linear SVM.

These courses provide insights into working with kernels and non-linear SVMs.

These books are excellent resources for understanding kernel methods in depth.

You may also find these topics relevant:

Mathematical Formulation of Hard/Soft Margins

When an SVM attempts to find a separating hyperplane, there are two main approaches regarding how strictly it enforces the separation: hard-margin and soft-margin classification.

Hard-margin SVM: This formulation is used when the training data is perfectly linearly separable. The goal is to find a hyperplane that maximizes the margin while ensuring that every data point is correctly classified and lies on the correct side of the margin (i.e., no points fall within the margin or on the wrong side). Mathematically, this translates to constraints where for each data point x_i with label y_i (where y_i is +1 or -1), y_i(w·x_i + b) ≥ 1. The objective is to minimize ||w||²/2 (which is equivalent to maximizing the margin 2/||w||) subject to these constraints. While theoretically clean, hard-margin SVMs are sensitive to outliers and may not find a solution if the data is not perfectly separable. Soft-margin SVM: In most real-world scenarios, data is not perfectly linearly separable, or there might be noisy data points (outliers) that make perfect separation undesirable as it could lead to overfitting. The soft-margin SVM addresses this by allowing some data points to be misclassified or to fall within the margin. This is achieved by introducing "slack variables" (ξ_i ≥ 0) into the optimization problem. The constraints become y_i(w·x_i + b) ≥ 1 - ξ_i.

The objective function is then modified to include a penalty for these slack variables: minimize ||w||²/2 + C Σξ_i. The parameter 'C' is a regularization parameter that controls the trade-off between maximizing the margin and minimizing the classification error (represented by the sum of slack variables). A small 'C' allows for a wider margin but more misclassifications (a "softer" margin), while a large 'C' pushes for fewer misclassifications, potentially leading to a narrower margin and a model that might overfit noisy data (a "harder" soft margin). The soft-margin formulation is far more practical and widely used.

This topic delves specifically into soft-margin SVMs.

SVM Algorithms and Variations

Support Vector Machines are not a one-size-fits-all solution. Different implementations and variations of the core SVM algorithm have been developed to address various types of data and machine learning tasks. This section explores some of these key distinctions and extensions.

Linear SVM vs. Non-linear SVM Implementations

The primary distinction in SVM implementations lies in how they handle the separability of data: linearly or non-linearly.

Linear SVMs are used when the data is linearly separable, meaning that the different classes can be divided by a single straight line (in 2D), a flat plane (in 3D), or a hyperplane (in higher dimensions). In such cases, the SVM algorithm directly finds the optimal hyperplane that maximizes the margin between the classes without needing to transform the data. Linear SVMs are generally faster to train and computationally less intensive than their non-linear counterparts. They are also more straightforward to interpret since the decision boundary is a simple linear function of the input features. Non-linear SVMs are employed when the data is not linearly separable in its original feature space. As discussed previously, these SVMs use the kernel trick to implicitly map the data into a higher-dimensional space where a linear separation becomes feasible. By choosing an appropriate kernel function (e.g., polynomial, RBF, sigmoid), non-linear SVMs can model complex decision boundaries that are curved or intricate in the original input space. While more powerful for complex datasets, non-linear SVMs can be more computationally demanding and require careful selection and tuning of the kernel function and its parameters to avoid overfitting.

The choice between a linear and non-linear SVM depends heavily on the nature of the data. If a linear boundary is sufficient, a linear SVM is often preferred for its simplicity and efficiency. For more complex patterns, a non-linear SVM with an appropriate kernel is necessary.

These courses cover both linear and non-linear SVM implementations and their practical use.

For a deeper dive into linear SVMs, consider this topic:

Multi-class Classification Techniques (One-vs-One, One-vs-All)

Standard SVMs are inherently binary classifiers, meaning they are designed to distinguish between two classes. However, many real-world problems involve classifying data into more than two categories (multi-class classification). Several strategies have been developed to extend SVMs for multi-class tasks. The two most common approaches are:

One-vs-Rest (OvR) or One-vs-All (OvA): In this strategy, for a problem with 'K' classes, 'K' separate binary SVM classifiers are trained. Each classifier is trained to distinguish the data points of one class from the data points of all other remaining classes (the "rest"). When a new, unseen data point needs to be classified, it is passed through all 'K' classifiers. Each classifier outputs a decision value (e.g., its distance to the hyperplane). The class corresponding to the classifier that outputs the highest decision value (or is most confident in its prediction) is typically chosen as the final prediction. One-vs-One (OvO): This approach involves constructing a binary SVM classifier for every pair of classes. For a problem with 'K' classes, this results in K*(K-1)/2 classifiers. Each classifier is trained on data only from the two classes it is designed to distinguish. To classify a new data point, it is presented to all these binary classifiers. Each classifier "votes" for one of the two classes it was trained on. The class that receives the most votes across all classifiers is then assigned as the final prediction.

The OvO strategy generally requires training more classifiers than OvR, especially as the number of classes increases. However, each OvO classifier is trained on a smaller subset of the data, which can sometimes be faster and more efficient. The performance of OvR versus OvO can vary depending on the dataset and the specific SVM implementation. Some SVM libraries, like scikit-learn, handle multi-class classification internally, allowing users to specify the strategy.

This course may touch upon multi-class classification strategies within the context of machine learning.

Support Vector Regression (SVR) Applications

While SVMs are most famously known for classification, a variation called Support Vector Regression (SVR) adapts the core principles for regression tasks, where the goal is to predict a continuous output value rather than a class label.

Similar to classification SVMs, SVR aims to find a function (a hyperplane in the feature space) that best fits the data. However, instead of maximizing the margin between classes, SVR tries to fit as many data points as possible within a certain margin (defined by a parameter called epsilon, ε) around the regression function. Data points that fall within this epsilon-tube do not contribute to the loss function. Points outside this tube are penalized, and the penalty increases with their distance from the tube.

The "support vectors" in SVR are the data points that lie on or outside the boundary of this epsilon-tube. The regression function is determined by these support vectors. Like classification SVMs, SVR can also utilize the kernel trick to model non-linear relationships between the input features and the continuous output variable.

SVR differs from traditional linear regression in that it doesn't assume a specific relationship that needs to be understood beforehand; SVR can discover these relationships on its own. It is often used in applications like time series prediction, financial forecasting, and other problems where predicting a continuous value is the objective.

These resources provide more information on Support Vector Regression:

This book offers a comprehensive look at SVMs, including their regression applications.

Recent Algorithmic Improvements and Variants

Research in Support Vector Machines is an ongoing field, leading to various algorithmic improvements and specialized variants designed to address specific challenges or enhance performance.

One area of improvement focuses on scalability. Training SVMs, especially non-linear SVMs with large datasets, can be computationally intensive due to the need to solve a quadratic programming problem. Researchers have developed faster training algorithms, such as Sequential Minimal Optimization (SMO) and its variants, as well as techniques for parallelizing SVM training or approximating the solution for very large datasets.

Other variants include:

• ν-SVM (Nu-SVM): This formulation, also for classification and regression, uses a different hyperparameter, ν (nu), which provides an upper bound on the fraction of training errors and a lower bound on the fraction of support vectors. This can sometimes offer a more intuitive way to control the number of support vectors.
• One-Class SVM: Used for novelty detection or outlier detection. It learns a boundary that encloses the "normal" data points. Any new data point falling outside this boundary is considered an anomaly.
• Structured SVMs (S-SVMs): Extend SVMs to handle structured outputs, such as sequences, trees, or graphs, rather than simple scalar or categorical labels. This is useful in areas like natural language processing (e.g., sequence labeling) and computer vision (e.g., image segmentation).
• Transductive SVMs (TSVMs): These are used in semi-supervised learning scenarios where, in addition to labeled data, there is a significant amount of unlabeled data available during training. TSVMs try to find a decision boundary that not only separates the labeled data but also respects the underlying structure of the unlabeled data, often by trying to place the boundary in low-density regions of the combined dataset. Vladimir N. Vapnik introduced transductive SVMs in 1998.

These advancements continue to expand the applicability and efficiency of SVMs in various machine learning domains.

Exploring recent research papers and advanced machine learning courses can provide deeper insights into these cutting-edge developments. The Artificial Intelligence section on OpenCourser might list courses that cover such advanced topics.

Applications in Industry and Research

Support Vector Machines, owing to their robustness and versatility, have found applications across a multitude of industries and research domains. Their ability to handle high-dimensional data and model complex, non-linear relationships makes them a valuable tool for solving real-world problems.

Biomedical Data Classification

In the biomedical field, SVMs are extensively used for various classification tasks. One prominent application is in medical diagnosis, where SVMs can be trained on patient data (including clinical measurements, imaging data, and genomic information) to predict the presence or absence of diseases. For instance, SVMs have been employed to classify different types of cancer, predict heart disease, or identify neurological disorders based on MRI images or EEG signals.

SVMs have also shown success in protein classification and remote homology detection, achieving high accuracy in identifying the functional categories of proteins based on their sequence or structural features. Another application area is in drug discovery, where SVMs can help predict the bioactivity of chemical compounds or identify potential drug targets. The ability of SVMs to handle complex, high-dimensional biological datasets is a key reason for their adoption in this field.

These courses provide a glimpse into how machine learning, including techniques like SVM, is applied in biomedical contexts.

Financial Market Prediction Models

The financial industry leverages machine learning, including SVMs, for various predictive modeling tasks. SVMs can be applied to predict stock market movements, such as forecasting whether a stock price will rise or fall, or predicting market volatility. While financial markets are notoriously complex and influenced by numerous factors, SVMs can attempt to identify patterns in historical price data, trading volumes, economic indicators, and even news sentiment to make these predictions.

Another application is in credit scoring and fraud detection. SVMs can be trained on customer data to assess creditworthiness or to identify potentially fraudulent transactions by learning patterns associated with legitimate and fraudulent activities. Support Vector Regression (SVR) can also be used for tasks like predicting asset prices or forecasting economic indicators. The robustness of SVMs to noisy data can be an advantage in the often-volatile financial domain.

Image Recognition and Computer Vision

Support Vector Machines have a strong presence in the field of image recognition and computer vision. They are used for tasks such as object detection and classification, where the goal is to identify and categorize objects within an image (e.g., distinguishing between cats and dogs, or identifying different types of vehicles). SVMs can be trained on features extracted from images, such as SIFT (Scale-Invariant Feature Transform) features or HOG (Histogram of Oriented Gradients) features.

Handwritten digit recognition is another classic application where SVMs have demonstrated high accuracy, playing a role in systems like postal mail sorting. Face detection and recognition systems also utilize SVMs to identify faces in images or videos and to verify identities. Even in medical imaging, SVMs are used to classify MRI images to detect anomalies like tumors. While deep learning models, particularly Convolutional Neural Networks (CNNs), have become dominant in many computer vision tasks, SVMs are still relevant, especially when training data is limited or for specific types of feature-based classification.

This course delves into computer vision, which often employs SVMs.

You might also be interested in these related topics:

Natural Language Processing Use Cases

In Natural Language Processing (NLP), SVMs have been widely applied to various text analysis tasks. One of the most common applications is text classification (also known as text categorization), where documents are assigned to predefined categories. Examples include:

• Spam detection: Classifying emails as spam or not spam.
• Sentiment analysis: Determining the sentiment (positive, negative, or neutral) expressed in a piece of text, such as a product review or a social media post.
• Topic categorization: Assigning news articles, blog posts, or research papers to specific topics.

SVMs are effective for text classification because text data can often be represented in very high-dimensional spaces (e.g., using bag-of-words models where each dimension corresponds to a word in the vocabulary), and SVMs are known to perform well in such scenarios. They can learn complex relationships between word patterns and document categories. The "kernel trick" also allows them to capture non-linear patterns in text data.

This book specifically addresses the use of SVMs for text classification.

This topic is central to many SVM applications in text.

Educational Pathways in SVM

Embarking on a journey to understand and utilize Support Vector Machines involves a combination of theoretical learning and practical application. Whether you are a student exploring machine learning or a professional looking to upskill, several educational pathways can lead to SVM expertise. Online courses, in particular, offer flexible and accessible routes to acquiring this knowledge.

University Programs with Machine Learning Focus

Many universities worldwide offer undergraduate and graduate programs in Computer Science, Data Science, Artificial Intelligence, or Statistics that include comprehensive coursework in machine learning, often featuring Support Vector Machines as a key topic. These programs provide a strong theoretical foundation, covering the mathematical underpinnings (linear algebra, calculus, probability, optimization) and algorithmic details of SVMs and other machine learning models.

Students in such programs typically engage in projects and research that allow them to apply SVMs to real-world datasets. Look for programs that emphasize practical experience and offer specializations in areas where SVMs are heavily used, such as bioinformatics, computer vision, or natural language processing. University settings also provide opportunities for collaboration with faculty and peers, which can be invaluable for deep learning and exploring advanced concepts. For those considering a career pivot, enrolling in a relevant Master's program can provide the necessary credentials and in-depth knowledge. While a significant commitment, it offers a structured and thorough path to expertise.

Core Mathematics Prerequisites for SVM Mastery

A solid grasp of certain mathematical concepts is crucial for truly understanding and effectively utilizing Support Vector Machines. While you can use SVM libraries without deep mathematical knowledge, a strong foundation will enable you to better understand model behavior, troubleshoot issues, choose appropriate parameters, and even contribute to algorithmic advancements.

The core prerequisites include:

• Linear Algebra: Essential for understanding vector spaces, dot products, matrix operations, and transformations, all ofwhich are fundamental to how SVMs define hyperplanes and manipulate data.
• Calculus (Multivariable): Needed for understanding optimization, particularly concepts like gradients and partial derivatives, which are used in the process of finding the optimal hyperplane.
• Optimization Theory: Concepts like constrained optimization, Lagrange multipliers, and convex optimization are at the heart of SVM training.
• Probability and Statistics: Important for understanding the broader context of machine learning, data distributions, model evaluation, and concepts like overfitting.

Many online courses and university programs focusing on machine learning will cover these prerequisites or expect students to have prior knowledge. For individuals transitioning into this field, dedicating time to strengthen these mathematical foundations is a worthwhile investment. It might seem daunting, but approaching these topics systematically, perhaps through dedicated online courses, can make them accessible. Remember, building a strong foundation takes time and effort, but it pays off in deeper understanding and capability.

This course is designed for beginners in AI and covers relevant linear algebra concepts.

This book delves into the statistical theory that forms the basis of SVMs.

Research Opportunities in Optimization Theory

For those with a strong mathematical aptitude and interest in pushing the boundaries of SVMs and related algorithms, research opportunities in optimization theory abound. The training of SVMs is fundamentally an optimization problem, often a quadratic programming (QP) problem. While standard solvers exist, developing more efficient and scalable optimization algorithms for SVMs, especially for very large datasets or specialized SVM variants, remains an active area of research.

This includes exploring:

• Faster solvers for large-scale SVMs: Developing algorithms that can handle datasets with millions or even billions of data points and features.
• Distributed and parallel optimization techniques: Designing methods to train SVMs across multiple processors or machines.
• Stochastic optimization methods: Adapting techniques like stochastic gradient descent (SGD) for SVM training, which can be more efficient for large datasets.
• Optimization for specific kernel types or SVM variants: Tailoring optimization approaches for particular problem structures or newer SVM formulations like deep kernel learning or multiple kernel learning.
• Theoretical analysis of optimization algorithms: Proving convergence rates and understanding the properties of different optimization strategies for SVMs.

Engaging in research in this area typically requires a strong background in mathematics, computer science, and machine learning, often at the graduate (Ph.D.) level. It offers the chance to contribute to the fundamental algorithms that power many machine learning applications.

Integration with Data Science Curricula

Support Vector Machines are a staple in modern data science curricula, reflecting their importance as a versatile and powerful classification and regression tool. Data science programs, whether at universities or through online platforms and bootcamps, almost invariably cover SVMs as part of their machine learning modules.

In these curricula, SVMs are typically introduced after foundational concepts in statistics, programming (often Python), and basic machine learning principles (like supervised vs. unsupervised learning, model evaluation). Students learn:

• The theoretical basis of SVMs: hyperplanes, margins, support vectors, and the kernel trick.
• Practical implementation: Using libraries like Scikit-learn in Python to train, test, and tune SVM models.
• Parameter tuning: Understanding how to select appropriate kernels (linear, RBF, polynomial, etc.) and tune hyperparameters like 'C' (regularization) and 'gamma' (for RBF kernels) to optimize performance.
• Applications: Working on projects that apply SVMs to various datasets from different domains (e.g., text classification, image analysis, bioinformatics).
• Comparison with other models: Understanding when to choose SVMs over other algorithms like logistic regression, decision trees, or neural networks.

Online courses are an excellent way for aspiring data scientists to learn about SVMs. Many platforms offer specialized machine learning courses or comprehensive data science tracks that include detailed modules on SVMs, often with hands-on coding exercises and projects. This makes learning accessible and allows individuals to build practical skills at their own pace. For those new to data science, starting with foundational Python and statistics courses before diving into machine learning algorithms like SVMs is a recommended path. OpenCourser's Learner's Guide can provide valuable tips on structuring your self-learning journey.

We think these courses provide a good introduction to SVMs within a broader machine learning or data science context.

These books are often considered foundational in machine learning and cover SVMs extensively.

Career Progression with SVM Expertise

Developing expertise in Support Vector Machines can open doors to various roles and specialization paths within the rapidly growing fields of machine learning and artificial intelligence. As SVMs are a fundamental and widely applied algorithm, proficiency in their theory and application is a valuable asset for professionals at different career stages.

Entry-Level Roles Requiring SVM Knowledge

For individuals starting their careers in machine learning or data science, knowledge of SVMs can be a significant advantage when applying for entry-level positions. Roles such as Junior Data Scientist, Machine Learning Engineer (entry-level), Data Analyst (with a machine learning focus), or AI Research Assistant often list SVMs as a desired or required skill.

In these roles, you might be expected to:

• Preprocess and clean data for SVM models.
• Implement SVM classifiers and regressors using libraries like Scikit-learn in Python.
• Perform hyperparameter tuning to optimize SVM performance.
• Evaluate model accuracy and other relevant metrics.
• Assist senior team members in developing and deploying machine learning solutions that may involve SVMs.
• Contribute to tasks like text classification, image analysis, or predictive modeling where SVMs are applicable.

A strong portfolio of projects demonstrating practical experience with SVMs, perhaps through online courses, university projects, or personal initiatives, can greatly enhance your employability for these entry-level positions. Even if a role doesn't exclusively focus on SVMs, understanding this core algorithm demonstrates a solid foundation in machine learning principles. For those transitioning careers, focusing on building such a portfolio through practical, hands-on learning is key. Don't be discouraged if the initial learning curve seems steep; consistent effort in applying these concepts will build confidence and competence.

These courses are excellent for building practical SVM skills for entry-level roles.

Specialization Paths in Machine Learning Engineering

As machine learning engineers gain experience, they often choose to specialize in particular areas. Expertise in SVMs can contribute to several specialization paths:

• Classical Machine Learning Specialist: Focusing on a deep understanding and application of a wide range of traditional ML algorithms, including SVMs, decision trees, ensemble methods, etc., for various predictive modeling tasks.
• NLP Engineer: Specializing in building systems that understand and process human language. SVMs are still relevant for tasks like text classification and sentiment analysis, complementing newer deep learning approaches.
• Computer Vision Engineer: Working on image and video analysis. While deep learning is dominant, SVMs can still be used for specific feature-based recognition tasks or in hybrid approaches.
• MLOps Engineer: Focusing on the deployment, monitoring, and maintenance of machine learning models in production. Understanding the characteristics of SVMs (e.g., computational cost, memory usage) is important for efficient deployment.
• Algorithm Optimization Specialist: For those with a strong mathematical background, specializing in optimizing the performance and scalability of machine learning algorithms, including SVMs, can be a niche area.

Continuous learning is crucial in machine learning. As you progress, supplementing your SVM knowledge with expertise in other algorithms, deep learning frameworks, and MLOps tools will broaden your career options. Consider exploring advanced courses and certifications relevant to your chosen specialization. OpenCourser can be a great resource for finding courses to develop professionally.

Research Positions in AI Development

A deep understanding of SVMs, particularly their mathematical foundations and advanced variants, is highly valuable for research positions in AI development. These roles are typically found in academic institutions, corporate research labs, and specialized AI companies.

Researchers in AI development might work on:

• Developing novel SVM algorithms or improving existing ones (e.g., for better scalability, handling specific data types, or new application areas).
• Exploring the theoretical properties of SVMs and kernel methods.
• Applying SVMs to challenging research problems in fields like bioinformatics, drug discovery, climate science, or fundamental physics.
• Integrating SVMs with other AI techniques, such as deep learning or reinforcement learning, to create hybrid models.
• Investigating the ethical implications and fairness of SVM-based systems.

These positions usually require an advanced degree (Master's or, more commonly, a Ph.D.) in computer science, statistics, mathematics, or a related field with a strong focus on machine learning research. A track record of publications in reputable conferences and journals is often essential. For those aspiring to such roles, pursuing graduate studies and actively engaging in research projects during their academic journey is the typical path.

This book provides insights into the theoretical underpinnings crucial for research.

You may also be interested in the broader topic of Artificial Intelligence research.

Career Growth Trajectories in AI-Driven Industries

Expertise in fundamental machine learning algorithms like SVMs provides a solid foundation for long-term career growth in the burgeoning AI-driven industries. As you accumulate experience and demonstrate impact, several growth trajectories can emerge:

• Senior Machine Learning Engineer / Lead Data Scientist: Taking on more complex projects, leading teams, mentoring junior members, and influencing the technical direction of AI initiatives.
• AI/ML Architect: Designing scalable and robust machine learning systems and infrastructure, making high-level design choices about algorithms (including when and how to use SVMs alongside other models), data pipelines, and deployment strategies.
• Research Scientist / Principal Investigator: Leading cutting-edge research projects in academic or industrial settings, pushing the boundaries of AI and machine learning.
• Product Manager (AI/ML): Combining technical understanding with business acumen to define the vision and strategy for AI-powered products, translating customer needs into technical requirements for engineering teams.
• Entrepreneur / Founder: Leveraging AI expertise to start a new venture that solves a specific problem using machine learning, potentially incorporating SVM-based solutions.
• Management/Leadership Roles: Moving into positions like Head of Data Science, Director of AI, or Chief Technology Officer (CTO), overseeing the AI strategy and teams within an organization.

The path to these roles often involves continuous learning, staying updated with the latest advancements in AI (including and beyond SVMs), developing strong problem-solving and communication skills, and gaining experience in applying AI to solve real-world business or scientific challenges. Building a strong professional network and seeking mentorship can also be invaluable. The journey in AI is dynamic and requires adaptability, but the foundational knowledge of algorithms like SVMs will remain relevant.

Consider exploring courses on leadership and management to complement your technical skills as you aim for higher roles. OpenCourser's Management category might have relevant options.

Challenges in SVM Implementation

While Support Vector Machines are powerful tools, practitioners can encounter several challenges during their implementation and deployment. Awareness of these potential hurdles can help in strategizing and mitigating them effectively.

Scalability Issues with Large Datasets

One of the most significant challenges with SVMs, particularly non-linear SVMs using kernel functions, is their scalability to very large datasets. The computational complexity of training an SVM can be high. Traditional SVM training algorithms often involve solving a quadratic programming (QP) problem whose complexity can range from O(n²) to O(n³), where 'n' is the number of training samples. The memory requirement can also be O(n²) to store the kernel matrix if it's precomputed.

For datasets with hundreds of thousands or millions of samples, standard SVM training can become prohibitively slow and resource-intensive. While more efficient training algorithms like Sequential Minimal Optimization (SMO) have been developed, and techniques like random sampling or using linear SVMs (which scale better) can be employed, scalability remains a key consideration. Researchers continue to work on developing faster and more scalable SVM training methods, including parallel and distributed approaches, and approximations that trade some accuracy for speed.

When faced with very large datasets, practitioners might need to:

• Consider using Linear SVMs if the data is high-dimensional and a linear separation is plausible.
• Explore approximate SVM solvers or online learning variants.
• Subsample the data, though this might lead to a loss of information.
• Utilize hardware acceleration (e.g., GPUs) if supported by the SVM library.

Kernel Selection and Parameter Tuning

For non-linear SVMs, the choice of the kernel function (e.g., linear, polynomial, RBF, sigmoid) and the tuning of its associated hyperparameters, along with the regularization parameter 'C', are critical for achieving good performance. This process can be challenging and time-consuming.

Kernel Selection: There's no universally best kernel. The RBF kernel is a popular default choice because of its flexibility in mapping data to a high-dimensional space and its ability to handle complex relationships. However, it might not always be the optimal choice. A linear kernel is preferred if the data is linearly separable or if the number of features is very large compared to the number of samples. Polynomial kernels can be useful for problems where polynomial relationships are expected. The choice often depends on domain knowledge and empirical experimentation. Parameter Tuning: Each kernel has its own set of parameters (e.g., 'gamma' for the RBF kernel, 'degree' for the polynomial kernel). These, along with the regularization parameter 'C' (which controls the trade-off between margin maximization and misclassification penalty), must be carefully tuned. Poorly chosen parameters can lead to underfitting (the model is too simple and performs poorly) or overfitting (the model learns the training data too well, including noise, and fails to generalize to new data). Techniques like grid search or randomized search, combined with cross-validation, are commonly used to find good hyperparameter values, but these can be computationally expensive.

This often requires an iterative process of training models with different parameter combinations and evaluating their performance on a validation set. Automated machine learning (AutoML) tools are also emerging to help automate this process.

These courses cover practical aspects of model selection and tuning, which are crucial for SVMs.

This book is a seminal text on kernel methods, providing deep insights into their selection and use.

Computational Complexity Considerations

Beyond the training phase, the computational complexity of making predictions (the test phase) with an SVM also needs consideration, though it's generally less of a concern than training complexity. For a linear SVM, prediction is fast, involving a simple dot product. For a kernelized SVM, the prediction time depends on the number of support vectors. In the worst case, all training points could become support vectors, making prediction time proportional to the number of training samples. However, SVMs are known for producing sparse solutions, meaning the number of support vectors is often much smaller than the total number of training samples, which helps keep prediction times manageable.

The complexity of evaluating the kernel function itself also contributes to the prediction time. Some kernels are more computationally intensive than others. For applications requiring very low-latency predictions, these factors might become important. Furthermore, storing the support vectors and their corresponding weights (alpha values) requires memory. While generally memory-efficient due to sparsity, this can be a factor for models with a very large number of support vectors deployed on resource-constrained devices.

Handling Imbalanced Datasets

Standard SVMs can perform poorly on imbalanced datasets, where one class has significantly more samples than another. This is because the optimization process aims to find a hyperplane that separates the classes, and with a large class imbalance, the classifier might become biased towards the majority class, leading to poor performance on the minority class. The hyperplane might be pushed towards the minority class, resulting in many misclassifications for that class, even if the overall accuracy appears high.

Several techniques can be used to address class imbalance with SVMs:

• Adjusting Class Weights: Many SVM implementations allow you to assign different weights to different classes. By assigning a higher weight to the minority class, you penalize misclassifications of minority class samples more heavily during training, forcing the SVM to pay more attention to them.
• Resampling Techniques:
  • Oversampling the minority class (e.g., by duplicating samples or generating synthetic samples using techniques like SMOTE - Synthetic Minority Over-sampling Technique).
  • Undersampling the majority class (e.g., by randomly removing samples).

  Care must be taken with resampling, as oversampling can lead to overfitting, and undersampling can lead to loss of information.

• Using Different Performance Metrics: Instead of accuracy, use metrics like precision, recall, F1-score, or the area under the ROC curve (AUC), which provide a better picture of performance on imbalanced datasets.
• One-Class SVM: If the goal is primarily to identify the minority class as an anomaly, a one-class SVM trained on the majority class might be an option.

Choosing the right strategy often involves experimentation and depends on the specific characteristics of the dataset and the problem at hand.

This course might cover techniques for handling imbalanced data within a broader machine learning context.

Future Trends in SVM Development

Support Vector Machines, despite being a well-established class of algorithms, continue to be an area of active research and development. Several exciting trends suggest that SVMs will remain relevant and evolve further, adapting to new computational paradigms and integrating with other advanced AI techniques.

Integration with Deep Learning Architectures

One of the most significant trends in machine learning is the rise of deep learning. While SVMs and deep neural networks have often been seen as distinct approaches, there's growing interest in integrating them to leverage the strengths of both.

For example, features extracted by the intermediate layers of a deep neural network (which are often highly informative and abstract representations of the input data) can be used as input to an SVM classifier. This hybrid approach can sometimes lead to improved performance, especially when the amount of labeled data for training the final classification layer of a deep network is limited. The SVM can act as a robust and effective classifier on top of powerful deep-learned features.

Another area is "deep kernel learning," where kernel functions themselves are learned using neural networks, allowing for the creation of highly adaptive and problem-specific kernels for SVMs. This blurs the lines between traditional kernel methods and deep learning, potentially leading to more powerful and flexible models. Research also explores using SVM-related concepts, like the margin maximization principle, to improve the training or architecture of deep neural networks.

Quantum Computing Applications

The emergence of quantum computing opens up new possibilities for accelerating machine learning algorithms, and SVMs are no exception. Researchers are actively exploring Quantum Support Vector Machines (QSVMs). The idea is that certain computationally intensive parts of the SVM algorithm, particularly those involving linear algebra operations in high-dimensional feature spaces (as implicitly handled by kernels), could potentially be performed much faster on a quantum computer.

For instance, quantum algorithms have been proposed for tasks like solving systems of linear equations or performing inner product estimations, which are relevant to SVM training and prediction. If realized, QSVMs could offer significant speedups for training SVMs on very large datasets or for using extremely complex kernels that are currently intractable. While quantum computing is still in its early stages, and practical, large-scale quantum computers are not yet widely available, the theoretical work on QSVMs is a promising avenue for future high-performance machine learning.

You might find this topic interesting if you're curious about the intersection of quantum computing and SVMs.

Automated Hyperparameter Optimization

As mentioned earlier, selecting the right kernel and tuning the hyperparameters of an SVM (like 'C' and 'gamma') is crucial for performance but can be a tedious and computationally expensive process. A significant trend is the development and adoption of more sophisticated techniques for automated hyperparameter optimization (AutoML for HPO).

While traditional methods like grid search and random search are commonly used, more advanced Bayesian optimization techniques, genetic algorithms, and gradient-based optimization methods are being applied to find optimal hyperparameters more efficiently. These methods intelligently explore the hyperparameter space, learning from past evaluations to guide future searches towards promising regions.

The goal is to make SVMs (and other machine learning models) easier to use and more accessible, even for non-experts, by automating one of the most challenging aspects of model development. As AutoML tools become more mature and integrated into machine learning libraries, we can expect the process of deploying high-performing SVM models to become significantly streamlined. This allows data scientists to focus more on problem formulation, feature engineering, and model interpretation rather than exhaustive manual tuning.

Ethical AI Implications of SVM Systems

As with all AI and machine learning systems, the development and deployment of SVMs raise important ethical considerations. While SVMs themselves are mathematical algorithms, how they are trained and used can have significant societal impacts.

Key ethical concerns include:

• Bias and Fairness: If the training data for an SVM reflects existing societal biases (e.g., in loan applications, hiring, or criminal justice), the SVM model can learn and even amplify these biases. This can lead to unfair or discriminatory outcomes for certain demographic groups. Ensuring fairness in SVMs requires careful attention to data collection, preprocessing techniques to mitigate bias, and the use of fairness-aware machine learning algorithms or post-processing adjustments.
• Transparency and Interpretability: While linear SVMs are relatively interpretable, non-linear SVMs using complex kernels can be "black boxes," making it difficult to understand why a particular decision was made. This lack of transparency can be problematic in critical applications (e.g., medical diagnosis, legal settings) where understanding the reasoning behind a prediction is crucial. Research into model interpretability techniques for SVMs is ongoing.
• Accountability: Determining who is responsible when an SVM-based system makes an error or causes harm can be challenging. Establishing clear lines of accountability for the design, deployment, and oversight of SVM systems is essential.
• Data Privacy: SVMs are trained on data, and this data may contain sensitive personal information. Ensuring that data used for training SVMs is handled in a privacy-preserving manner, in compliance with regulations like GDPR, is critical.

The AI community is increasingly focused on developing principles and practices for responsible AI development. This includes building fairness, transparency, and accountability into SVMs and other machine learning models from the outset. For anyone working with SVMs, being aware of these ethical dimensions and striving to build systems that are not only accurate but also fair and responsible is paramount.

Further exploration into Ethics in AI can provide a broader context for these important considerations.

Frequently Asked Questions (Career Focus)

For those considering a career path involving Support Vector Machines, several practical questions often arise. This section aims to address some common queries to help guide your professional development in the SVM field.

Essential SVM skills for machine learning roles?

For machine learning roles involving SVMs, a combination of theoretical understanding and practical skills is essential. Key skills include:

• Understanding SVM Concepts: A solid grasp of core principles like hyperplanes, margins, support vectors, the kernel trick (linear, polynomial, RBF kernels), and soft/hard margin classification.
• Mathematical Foundations: Familiarity with the underlying linear algebra, calculus, and optimization theory.
• Python Programming: Proficiency in Python is crucial, as it's the most common language for machine learning.
• Scikit-learn Library: Hands-on experience with the Scikit-learn library for implementing SVMs (SVC, SVR, LinearSVC), including data preprocessing, model training, and prediction.
• Hyperparameter Tuning: Knowing how to tune SVM hyperparameters (e.g., 'C', 'kernel', 'gamma') using techniques like grid search, randomized search, and cross-validation to optimize model performance.
• Model Evaluation: Understanding and applying appropriate evaluation metrics for classification (accuracy, precision, recall, F1-score, AUC-ROC) and regression tasks, especially in the context of imbalanced datasets.
• Data Preprocessing: Skills in cleaning data, handling missing values, feature scaling (important for SVMs), and feature engineering.
• Problem-Solving: The ability to analyze a problem, determine if SVM is an appropriate tool, and implement a solution effectively.
• Communication Skills: Being able to explain complex SVM concepts and model results to both technical and non-technical audiences.

Building a portfolio of projects that showcase these skills is highly recommended.

These courses can help you build many of these essential practical skills.

Certifications vs. academic credentials debate?

The debate between the value of certifications and academic credentials (like degrees) in the machine learning field, including for SVM expertise, is ongoing and nuanced. Both can be valuable, but they often serve different purposes and are viewed differently by employers.

Academic Credentials (e.g., Bachelor's, Master's, Ph.D.):

• Provide a deep, foundational understanding of computer science, mathematics, statistics, and machine learning theory. This is crucial for R&D roles or positions requiring a strong theoretical background.
• Often involve in-depth projects, research, and a structured curriculum that covers a broad range of topics.
• Generally carry more weight for research-oriented positions or roles in more traditional, established companies.
• Can be a significant time and financial investment.

Certifications (e.g., from online platforms, software vendors):

• Tend to be more focused on specific skills, tools, or platforms (e.g., a certification in a particular cloud provider's ML services, or a specialization in a set of algorithms).
• Can be acquired more quickly and are often more affordable, making them accessible for career changers or those looking to upskill in a specific area.
• Demonstrate a commitment to continuous learning and can be a good way to gain practical, hands-on skills with specific technologies.
• May be highly valued for applied roles where practical skills with specific tools are paramount.

For roles heavily involving SVMs, a strong theoretical understanding (often gained through academic routes) combined with practical implementation skills (which can be honed through certifications and projects) is ideal. Many employers look for a combination of both. A degree might get your resume noticed, while projects and relevant certifications can demonstrate your practical abilities during the interview process. Ultimately, demonstrable skills and a strong portfolio of projects often speak loudest. OpenCourser offers a wide array of courses, some of which lead to certificates that can be added to your resume or LinkedIn profile. You can learn more about making the most of these in our Learner's Guide.

Industry demand for SVM specialists?

While the term "SVM specialist" might not be a common job title, professionals with strong expertise in SVMs and other classical machine learning algorithms are definitely in demand. SVMs are a fundamental tool in the machine learning toolkit, and their applications span various industries, including tech, finance, healthcare, e-commerce, and more.

The demand is often for broader roles like Machine Learning Engineer, Data Scientist, or AI Researcher, where SVMs are one of several techniques that a professional is expected to understand and apply. Industries value individuals who can:

• Choose the right algorithm (which might be an SVM) for a given problem.
• Implement, tune, and deploy SVM models effectively.
• Understand the trade-offs of using SVMs compared to other methods (e.g., deep learning models, decision trees).
• Apply SVMs to solve specific business problems like classification, regression, anomaly detection in their respective domains (e.g., fraud detection in finance, medical diagnosis in healthcare, text categorization in tech).

While newer techniques like deep learning have gained significant attention, classical machine learning algorithms like SVMs remain crucial, especially in scenarios with limited data, when interpretability is important, or for establishing baselines. Therefore, proficiency in SVMs enhances a candidate's profile and broadens their applicability in the job market. The demand is less for pure "SVM specialists" and more for versatile machine learning professionals who have SVMs as a strong component of their skillset.

Transitioning from SVM to broader AI expertise?

Expertise in SVMs provides an excellent foundation for transitioning to broader AI expertise. SVMs touch upon many core AI concepts: supervised learning, feature spaces, optimization, and model evaluation. To broaden your expertise, consider the following steps:

• Master Other Machine Learning Algorithms: Beyond SVMs, delve into decision trees, random forests, gradient boosting machines, clustering algorithms (e.g., K-means), and dimensionality reduction techniques (e.g., PCA). Understanding a wider range of algorithms allows you to choose the best tool for different problems.
• Explore Deep Learning: This is a major area of AI. Learn about neural networks, convolutional neural networks (CNNs) for image processing, recurrent neural networks (RNNs) and transformers for sequential data like text and time series. Many online platforms offer specializations in deep learning.
• Learn about Unsupervised and Reinforcement Learning: Expand beyond supervised learning (where SVMs primarily reside) to understand unsupervised methods (for finding patterns in unlabeled data) and reinforcement learning (for training agents to make decisions).
• Gain Domain Knowledge: Apply your AI skills to specific domains that interest you (e.g., healthcare, finance, robotics). Domain expertise helps in understanding the nuances of the data and the problem.
• MLOps and Deployment: Learn about the practical aspects of deploying and maintaining AI models in production, including version control, monitoring, and scaling.
• AI Ethics and Responsible AI: Understand the ethical implications of AI systems, including bias, fairness, and transparency.
• Stay Updated: The field of AI is rapidly evolving. Continuously read research papers, follow AI blogs and communities, and take new courses to keep your knowledge current. OpenCourser's blog, OpenCourser Notes, often features articles on new trends and learning strategies.

Your SVM knowledge, particularly the understanding of mathematical optimization and kernel methods, can provide unique insights even when learning seemingly different AI paradigms.

These topics are good starting points for broadening your AI knowledge.

Freelance opportunities in SVM consulting?

Yes, there can be freelance and consulting opportunities for individuals with strong SVM expertise, particularly if combined with broader data science and machine learning skills. Businesses of all sizes may require specialized knowledge for specific projects without needing to hire a full-time expert.

Opportunities might arise in areas such as:

• Developing custom machine learning models: For clients who need classification or regression solutions where SVMs are well-suited (e.g., text analysis, image-based classification for smaller datasets, anomaly detection).
• Optimizing existing SVM models: Helping clients improve the performance of their current SVM implementations through better feature engineering, hyperparameter tuning, or kernel selection.
• Data analysis and insights: Using SVMs as part of a broader data analysis project to extract insights from client data.
• Proof-of-concept projects: Building prototype SVM models to demonstrate the feasibility of a machine learning solution for a client's problem.
• Training and workshops: Providing training to company teams on SVMs and other machine learning techniques.

To succeed as a freelance SVM consultant, you'll typically need:

• A strong portfolio showcasing successful projects.
• Good communication and client management skills.
• The ability to understand business requirements and translate them into technical solutions.
• A broader skillset beyond just SVMs, as clients often have diverse needs.
• A professional network and potentially a presence on freelance platforms.

While "SVM-only" consulting might be niche, expertise in SVMs as part of a comprehensive machine learning consulting offering can certainly create freelance opportunities.

Impact of AI automation on SVM-related careers?

AI automation, including AutoML tools that automate parts of the machine learning pipeline (like model selection and hyperparameter tuning), will undoubtedly impact careers related to SVMs, but it's more likely to transform roles rather than eliminate them entirely.

Potential Impacts:

• Reduced need for manual tuning: AutoML can automate the tedious process of hyperparameter tuning for SVMs, freeing up practitioners to focus on higher-level tasks.
• Easier model selection: AutoML tools can quickly compare SVMs against other algorithms, helping to select the best model for a given task with less manual effort.
• Democratization: More people with less deep expertise might be able to use SVMs effectively with the help of automation tools.

Continued Need for Human Expertise:

• Problem Formulation: Defining the business problem and translating it into a machine learning task still requires human insight.
• Data Understanding and Feature Engineering: Understanding the data, cleaning it, and creating relevant features are critical steps where human expertise is invaluable and often has a greater impact on performance than model choice alone. SVM performance is highly dependent on good features.
• Interpreting Results and Debugging: Understanding why an SVM model makes certain predictions, diagnosing issues, and explaining results to stakeholders will remain crucial human skills, especially for complex non-linear SVMs.
• Handling Complex or Novel Problems: AutoML may struggle with highly specialized or novel applications of SVMs that require custom kernels or unique problem formulations.
• Ethical Considerations: Ensuring fairness, accountability, and transparency in SVM models requires human oversight and judgment that automation alone cannot provide.
• Research and Development: Pushing the boundaries of SVM algorithms and their applications will always require human researchers.

In essence, AI automation will likely handle more of the routine aspects of working with SVMs, allowing professionals to focus on more strategic, creative, and complex problem-solving. This means that a deeper understanding of the underlying principles of SVMs (and machine learning in general) will become even more important, as practitioners will need to guide, interpret, and validate the outputs of automated systems. Continuous learning and adapting to new tools will be key.

Getting Started with SVMs on OpenCourser

If this exploration of Support Vector Machines has piqued your interest, OpenCourser is an excellent resource to begin or continue your learning journey. With thousands of online courses and books, you can find materials tailored to your current knowledge level and learning goals.

You can start by exploring foundational courses in Machine Learning or Data Science to build a strong base. Many of these will introduce SVMs as a core topic. For more focused learning, you can search directly for courses on "Support Vector Machines" or "SVM." OpenCourser allows you to easily browse through thousands of courses, save interesting options to a list, compare syllabi, and read summarized reviews to find the perfect online course.

For those on a budget, don't forget to check the deals page for any limited-time offers on relevant online courses. Remember, the journey to mastering any complex topic is a marathon, not a sprint. Be patient with yourself, focus on consistent learning, and apply your knowledge through hands-on projects. Good luck!

Support Vector Machines offer a fascinating and powerful approach to classification and regression problems. From their solid mathematical foundations to their diverse applications across industries, SVMs represent a key algorithm in the machine learning landscape. Whether you are aiming to build a career in AI, enhance your data science skills, or simply explore the intricacies of machine learning, understanding SVMs is a valuable endeavor. The path to expertise requires dedication to learning both the theory and practical implementation, but the rewards, in terms of problem-solving capabilities and career opportunities, can be substantial.