Doğrusal Cebir I: Uzaylar ve İşlemciler / Linear Algebra I: Spaces and Operators from Coursera

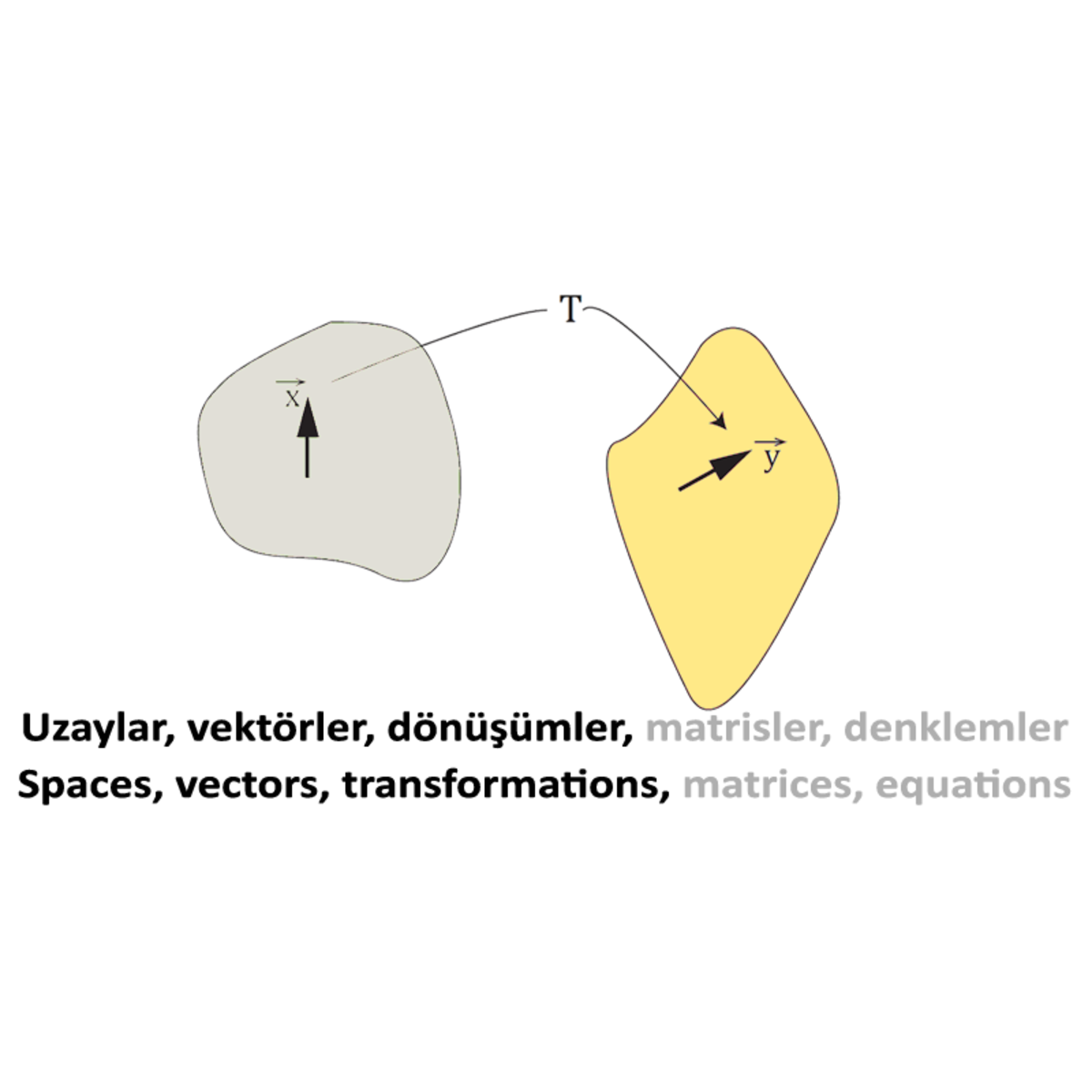
Bu ders doğrusal cebir ikili dizinin birincisidir. Doğrusal uzaylar kavramı, doğrusal işlemciler, matris gösterimleri ve denklem sistemlerinin hesaplanabilmesi için temel araçlar vb. konuları içermektedir. Ders gerçek yaşamdan gelen uygulamaları da tanıtmaya önem veren “içerikli yaklaşımla” tasarlanmıştır.

Bölümler:

Bölüm 1: Doğrusal Cebirin Matematikdeki Yeri ve Kapsamı

Bölüm 2: Düzlemdeki Vektörlerin Öğrettikleri

Bölüm 3: İki Bilinmeyenli Denklemlerin Öğrettikleri

Bölüm 4: Doğrusal Uzaylar

Bölüm 5: Fonksiyon Uzayları ve Fourier Serileri

Bölüm 6: Doğrusal İşlemciler ve Dönüşümler

Bölüm 7: Doğrusal İşlemcilerden Matrislere Geçiş

Bölüm 8: Matris İşlemleri

-----------

This is the first of the sequence of two courses. It develops the fundamental concepts in linear spaces, linear operators, matrix representations and basic tools for calculations with systems of equations. The course is designed with a “content based” emphasis, answering the “why” and “where“ of the topics, as much as the traditional “what” and “how” leading to “definitions” and “proofs”.

Chapters:

Chapter 1: Place and Contents of Linear Algebra Cebirin

Chapter 2: Learning From Vectors in the Plane

Chapter 3: Learning From Equations For Two Unknowns

Chapter 4: Linear Spaces

Chapter 5: Function Spaces and Fourier Series

Chapter 6: Linear Operators and Transformations

Chapter 7: From Linear Operators to Matrices

Chapter 8: Matrix Operations

-----------

Kaynak: Attila Aşkar, “Doğrusal cebir”. Bu kitap dört ciltlik dizinin üçüncü cildidir. Dizinin diğer kitapları Cilt 1 “Tek değişkenli fonksiyonlarda türev ve entegral”, Cilt 2: "Çok değişkenli fonksiyonlarda türev ve entegral" ve Cilt 4: “Diferansiyel denklemler” dir.

Source: Attila Aşkar, Linear Algebra, Volume 3 of the set of Vol1: Calculus of Single Variable Functions, Volume 2: Calculus of Multivariable Functions and Volume 4: Differential Equations.

What's inside

Syllabus

Doğrusal Cebirin Matematikdeki Yeri ve Kapsamı / Place and Contents of Linear Algebra

Düzlemdeki Vektörlerin Öğrettikleri / Learning From Vectors in the Plane

İki Bilinmeyenli Denklemlerin Öğrettikleri / Learning From Equations for Two Unknowns

Doğrusal Uzaylar / Linear Spaces

Fonksiyon Uzayları ve Fourier Serileri / Function Spaces and Fourier Series

Doğrusal İşlemciler ve Dönüşümler / Linear Operators and Transformations

Doğrusal İşlemcilerden Matrislere Geçiş / From Linear Operators to Matrices

Matris İşlemleri / Matrix Operations

Good to know

Know what's good

, what to watch for

, and possible dealbreakers

Doğrusal uzaylar, doğrusal işlemler, matris gösterimleri, denklem sistemleri çözümleri gibi temel kavram ve araçları konu alır

Gerçek dünya örnekleriyle öğretimi destekleyerek, teorik bilgilerin pratikteki uygulamalarını vurgular

Kursiyerlerin matematiksel düşüncelerini geliştirmelerini, soyut kavramları kavramalarını sağlar

Matematik, fizik, mühendislik, bilgisayar bilimleri gibi alanlarda çalışanların temel bir ihtiyacını karşılar

Dört ciltlik bir kitap serisinin üçüncü bölümünü oluşturarak, kapsamlı bir matematik eğitim programının parçası haline gelir

Reviews summary

Linear algebra concepts and applications

Students find this course to be an excellent overview of the field of linear algebra. They frequently comment that they enjoyed learning about linear spaces, linear operators, matrix representations, and basic tools for calculations with systems of equations.

Helpful and friendly professor

"Excellent course, thank you very much to the lecturer!"

Clear explanations of linear algebra concepts

"It was nice... Thank you so much"

Activities

Be better prepared before your course. Deepen your understanding during and after it. Supplement your coursework and achieve mastery of the topics covered in Doğrusal Cebir I: Uzaylar ve İşlemciler / Linear Algebra I: Spaces and Operators with these activities:

Diğer öğrencilerle doğrusal cebir çalışın

Show steps

Doğrusal cebir kavramlarını diğer öğrencilerle tartışmanıza yardımcı olacaktır ve bu da anlayışınızı geliştirecektir.

Show steps

Bir çalışma grubu oluşturun
Doğrusal cebir problemlerini birlikte çözün
Kavramsal soruları tartışın

Doğrusal cebir kavramlarını açıklayın

Show steps

Doğrusal cebir kavramlarını daha derinlemesine anlamanıza yardımcı olacaktır ve bilgilerinizi pekiştirmenize yardımcı olacaktır.

Show steps

Doğrusal uzayların tanımını açıklayın
Doğrusal dönüşümlerin özelliklerini açıklayın
Doğrusal cebirin uygulamalarını tartışın

Diğer öğrencilere doğrusal cebir öğretin

Show steps

Doğrusal cebir kavramlarını anlamanıza ve bilginizi pekiştirmenize yardımcı olacaktır.

Show steps

Doğrusal cebirde yeteneklerinizi geliştirin
Diğer öğrencilere ders verin
Konuları açık bir şekilde iletin

Show all three activities

Career center

Learners who complete Doğrusal Cebir I: Uzaylar ve İşlemciler / Linear Algebra I: Spaces and Operators will develop knowledge and skills that may be useful to these careers:

Linear Algebra Teacher

Linear Algebra Teachers impart knowledge of matrix representations, linear spaces, and linear operators to high school and university students. They create lesson plans, develop and grade assignments, and provide feedback to students. This course provides a solid foundation in the fundamental concepts of linear algebra, which are essential for teaching the subject effectively. The course covers topics such as vector spaces, linear transformations, matrices, and eigenvalues and eigenvectors, which are all essential concepts for a Linear Algebra Teacher.

See salaries and explore the career path for Linear Algebra Teacher

Investment Analyst

Investment Analysts use linear algebra to analyze financial data, build models, and make investment recommendations. They use matrix operations to represent portfolios, calculate risk and return, and analyze trends. This course provides a strong foundation in the mathematical principles and concepts used in investment analysis, such as linear regression and matrix algebra. By understanding these concepts, Investment Analysts can make more informed and data-driven decisions.

See salaries and explore the career path for Investment Analyst

Data Scientist

Data Scientists use linear algebra to analyze large datasets, identify patterns, and build predictive models. They use matrix operations to represent data, perform statistical analysis, and visualize results. This course provides a strong foundation in the mathematical and computational techniques used in data science, such as linear regression, principal component analysis, and singular value decomposition. By understanding these concepts, Data Scientists can extract meaningful insights from complex data and make better predictions.

See salaries and explore the career path for Data Scientist

Operations Research Analyst

Operations Research Analysts use linear algebra to optimize systems and processes. They use matrix operations to model problems, develop algorithms, and analyze results. This course provides a strong foundation in the mathematical principles and techniques used in operations research, such as linear programming, network optimization, and decision analysis. By understanding these concepts, Operations Research Analysts can improve the efficiency and effectiveness of organizations.

See salaries and explore the career path for Operations Research Analyst

Quantitative Analyst

Quantitative Analysts use linear algebra to develop and implement mathematical models for financial markets. They use matrix operations to represent portfolios, calculate risk and return, and analyze trends. This course provides a foundation in the mathematical principles and concepts used in quantitative finance, such as linear regression and matrix algebra. By understanding these concepts, Quantitative Analysts can develop and implement more sophisticated models for financial markets.

See salaries and explore the career path for Quantitative Analyst

Financial Analyst

Financial Analysts use linear algebra to analyze financial data, build models, and make investment recommendations. They use matrix operations to represent portfolios, calculate risk and return, and analyze trends. This course provides a foundation in the mathematical principles and concepts used in financial analysis, such as linear regression and matrix algebra. By understanding these concepts, Financial Analysts can make more informed and data-driven decisions.

See salaries and explore the career path for Financial Analyst

Software Engineer

Software Engineers use linear algebra to develop and implement algorithms for a variety of applications. They use matrix operations to represent data structures, perform numerical calculations, and optimize performance. This course provides a foundation in the mathematical principles and techniques used in software engineering, such as linear algebra, calculus, and probability. By understanding these concepts, Software Engineers can develop and implement more efficient and effective software.

See salaries and explore the career path for Software Engineer

Actuary

Actuaries use linear algebra to analyze financial data, calculate risks, and make insurance recommendations. They use matrix operations to represent portfolios, calculate risk and return, and analyze trends. This course provides a foundation in the mathematical principles and concepts used in actuarial science, such as linear regression and matrix algebra. By understanding these concepts, Actuaries can make more informed and data-driven decisions.

See salaries and explore the career path for Actuary

Market Researcher

Market Researchers use linear algebra to analyze market data, identify trends, and forecast future demand. They use matrix operations to represent market data, perform statistical analysis, and visualize results. This course provides a foundation in the mathematical and statistical techniques used in market research, such as linear regression, principal component analysis, and conjoint analysis. By understanding these concepts, Market Researchers can extract meaningful insights from market data and make better predictions.

See salaries and explore the career path for Market Researcher

Economist

Economists use linear algebra to analyze economic data, build models, and make economic forecasts. They use matrix operations to represent economic data, perform statistical analysis, and visualize results. This course provides a foundation in the mathematical principles and techniques used in economics, such as linear regression, input-output analysis, and game theory. By understanding these concepts, Economists can develop and implement more sophisticated models for economic analysis.

See salaries and explore the career path for Economist

Operations Manager

Operations Managers use linear algebra to optimize systems and processes. They use matrix operations to model problems, develop algorithms, and analyze results. This course provides a foundation in the mathematical principles and techniques used in operations management, such as linear programming, network optimization, and decision analysis. By understanding these concepts, Operations Managers can improve the efficiency and effectiveness of organizations.

See salaries and explore the career path for Operations Manager

Computer Scientist

Computer Scientists use linear algebra to develop and implement algorithms for a variety of applications. They use matrix operations to represent data structures, perform numerical calculations, and optimize performance. This course provides a foundation in the mathematical principles and techniques used in computer science, such as linear algebra, calculus, and probability. By understanding these concepts, Computer Scientists can develop and implement more efficient and effective algorithms.

See salaries and explore the career path for Computer Scientist

Statistician

Statisticians use linear algebra to analyze data, develop models, and make predictions. They use matrix operations to represent data, perform statistical analysis, and visualize results. This course provides a foundation in the mathematical principles and techniques used in statistics, such as linear regression, principal component analysis, and discriminant analysis. By understanding these concepts, Statisticians can develop and implement more sophisticated models for data analysis.

See salaries and explore the career path for Statistician

Financial Risk Manager

Financial Risk Managers use linear algebra to analyze financial data, calculate risks, and make investment recommendations. They use matrix operations to represent portfolios, calculate risk and return, and analyze trends. This course provides a foundation in the mathematical principles and concepts used in financial risk management, such as linear regression and matrix algebra. By understanding these concepts, Financial Risk Managers can make more informed and data-driven decisions.

See salaries and explore the career path for Financial Risk Manager

Data Analyst

Data Analysts use linear algebra to analyze data, identify patterns, and build predictive models. They use matrix operations to represent data, perform statistical analysis, and visualize results. This course provides a foundation in the mathematical and computational techniques used in data analysis, such as linear regression, principal component analysis, and singular value decomposition. By understanding these concepts, Data Analysts can extract meaningful insights from complex data and make better predictions.

See salaries and explore the career path for Data Analyst