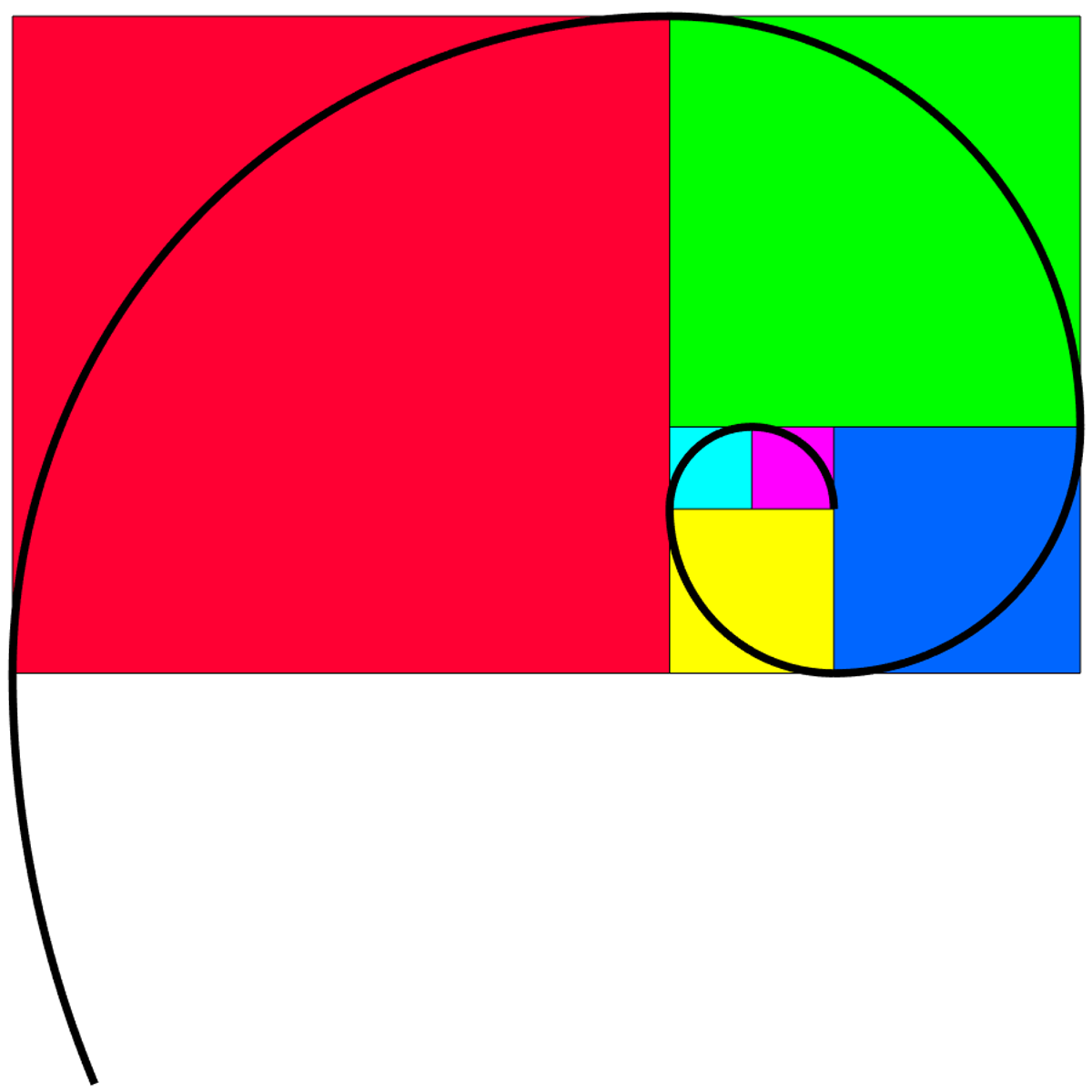
Learn the mathematics behind the Fibonacci numbers, the golden ratio, and their relationship to each other. These topics may not be taught as part of a typical math curriculum, but they contain many fascinating results that are still accessible to an advanced high school student.
The course culminates in an exploration of the Fibonacci numbers appearing unexpectedly in nature, such as the number of spirals in the head of a sunflower.
Download the lecture notes from the link
https://www.math.hkust.edu.hk/~machas/fibonacci.pdf
Watch the promotional video:
Read more
Learn the mathematics behind the Fibonacci numbers, the golden ratio, and their relationship to each other. These topics may not be taught as part of a typical math curriculum, but they contain many fascinating results that are still accessible to an advanced high school student.
The course culminates in an exploration of the Fibonacci numbers appearing unexpectedly in nature, such as the number of spirals in the head of a sunflower.
Download the lecture notes from the link
https://www.math.hkust.edu.hk/~machas/fibonacci.pdf
Watch the promotional video:
Learn the mathematics behind the Fibonacci numbers, the golden ratio, and their relationship to each other. These topics may not be taught as part of a typical math curriculum, but they contain many fascinating results that are still accessible to an advanced high school student.
The course culminates in an exploration of the Fibonacci numbers appearing unexpectedly in nature, such as the number of spirals in the head of a sunflower.
Download the lecture notes from the link
https://www.math.hkust.edu.hk/~machas/fibonacci.pdf
Watch the promotional video:
https://youtu.be/VWXeDFyB1hc
What's inside
Syllabus
Fibonacci: It's as easy as 1, 1, 2, 3
We learn about the Fibonacci numbers, the golden ratio, and their relationship. We derive the celebrated Binet's formula, which gives an explicit formula for the Fibonacci numbers in terms of powers of the golden ratio and its reciprocal. This formula can be used to calculate the nth Fibonacci number without having to sum the preceding terms in the sequence.
Read more
Syllabus
Good to know
Save this course
Reviews summary
Fibonacci and golden ratio: engaging math concepts
Activities
Participate in peer study sessions to discuss course concepts
Show steps
Engage in discussions with peers to clarify concepts, share insights, and foster a deeper understanding of the course material.
Show steps
-
Identify a peer or group of peers to study with.
-
Schedule regular study sessions.
-
Prepare for sessions by reviewing course notes and materials.
-
Actively participate in discussions, asking questions and sharing your own understanding.
Review the Fibonacci sequence
Show steps
Brush up on the basics of the Fibonacci sequence to strengthen your understanding of the topics covered in this course.
Show steps
-
Recall the definition of the Fibonacci sequence.
-
Generate the first 10 terms of the sequence.
Attend a workshop on the golden ratio in design
Show steps
Attend a workshop to learn how the golden ratio is used in design, and how you can apply it to your own work.
Browse courses on
Design
Show steps
-
Find a workshop on the golden ratio in design
-
Attend the workshop
Ten other activities
Expand to see all activities and additional details
Show all 13 activities
Read 'The Golden Ratio' by Mario Livio
Show steps
Review the book 'The Golden Ratio' to gain a comprehensive overview of its history, applications, and significance. This will deepen your understanding of the topic beyond the course material.
View
The Golden Ratio: The Story of PHI, the World's...
on Amazon
Show steps
-
Read the book, paying attention to the historical and cultural aspects of the golden ratio.
-
Take notes on the mathematical concepts and formulas related to the golden ratio.
Solve problems involving Fibonacci numbers and the Golden ratio
Show steps
Reinforce your problem-solving skills by tackling challenges that involve applying Fibonacci numbers and the Golden ratio, improving your proficiency.
Browse courses on
Fibonacci Numbers
Show steps
-
Find practice problems online or in textbooks.
-
Set aside dedicated time for solving the problems.
-
Check your solutions against provided answers or work with a tutor to verify your understanding.
Explore interactive visualizations of the Golden ratio
Show steps
Delve deeper into the Golden ratio through interactive visualizations, enhancing your comprehension of its properties and applications.
Show steps
-
Locate interactive visualizations of the Golden ratio online.
-
Explore the visualizations, observing how the Golden ratio manifests in various geometric forms.
Fibonacci Formula Practice
Show steps
Apply your knowledge of the Fibonacci Formula by completing a series of practice problems.
Browse courses on
Fibonacci Numbers
Show steps
-
Review the Fibonacci Formula: F(n) = F(n-1) + F(n-2)
-
Solve practice problems involving the Fibonacci Formula
-
Check your answers and identify areas for improvement
Fibonacci Problem-Solving Collaboration
Show steps
Engage in peer discussions and problem-solving sessions to deepen your understanding of Fibonacci-related concepts.
Browse courses on
Fibonacci Numbers
Show steps
-
Join or form a study group with other students
-
Discuss complex Fibonacci problems and share different approaches
-
Collaborate on solving challenging problems and provide constructive feedback
Golden Ratio in Nature
Show steps
Explore the fascinating applications of the Golden Ratio in nature, from the spiral patterns of seashells to the arrangement of leaves on a plant stem.
Show steps
-
Research the Golden Ratio and its significance in nature
-
Identify examples of the Golden Ratio in various natural phenomena
-
Analyze how the Golden Ratio contributes to the aesthetics and functionality of natural structures
Write a blog post about the applications of Fibonacci numbers
Show steps
Write a blog post to demonstrate your understanding of the applications of Fibonacci numbers in various fields, such as nature, art, and architecture.
Browse courses on
Applications
Show steps
-
Research the applications of Fibonacci numbers
-
Write a blog post outlining your findings
Create a visual representation of the Fibonacci spiral
Show steps
Solidify your understanding of the Fibonacci spiral by creating your own visual representation, fostering a deeper connection with the concept.
Show steps
-
Choose a method for creating your visual representation (e.g., drawing, digital art, physical model).
-
Plan the layout and incorporate the Fibonacci spiral into your design.
-
Execute your design, accurately representing the proportions and patterns of the Fibonacci spiral.
Fibonacci Sequence in Music
Show steps
Demonstrate your understanding of the Fibonacci Sequence by creating a piece of music that incorporates its principles.
Browse courses on
Fibonacci Numbers
Show steps
-
Study the Fibonacci Sequence and its mathematical properties
-
Compose a musical piece using the Fibonacci Sequence as a guide for note durations, rhythms, or melodic patterns
-
Share your musical composition with others for feedback and appreciation
Fibonacci Challenge
Show steps
Test your skills and knowledge by participating in a Fibonacci-themed competition or challenge.
Browse courses on
Fibonacci Numbers
Show steps
-
Identify and register for a suitable Fibonacci competition or challenge
-
Prepare thoroughly by studying Fibonacci-related concepts and practicing problem-solving
-
Compete in the challenge and strive for excellence
-
Reflect on your performance and identify areas for improvement
Participate in peer study sessions to discuss course concepts
Show steps
Engage in discussions with peers to clarify concepts, share insights, and foster a deeper understanding of the course material.
Show steps
- Identify a peer or group of peers to study with.
- Schedule regular study sessions.
- Prepare for sessions by reviewing course notes and materials.
- Actively participate in discussions, asking questions and sharing your own understanding.
Review the Fibonacci sequence
Show steps
Brush up on the basics of the Fibonacci sequence to strengthen your understanding of the topics covered in this course.
Show steps
- Recall the definition of the Fibonacci sequence.
- Generate the first 10 terms of the sequence.
Attend a workshop on the golden ratio in design
Show steps
Attend a workshop to learn how the golden ratio is used in design, and how you can apply it to your own work.
Browse courses on
Design
Show steps
- Find a workshop on the golden ratio in design
- Attend the workshop
Read 'The Golden Ratio' by Mario Livio
Show steps
Review the book 'The Golden Ratio' to gain a comprehensive overview of its history, applications, and significance. This will deepen your understanding of the topic beyond the course material.
View
The Golden Ratio: The Story of PHI, the World's...
on Amazon
Show steps
- Read the book, paying attention to the historical and cultural aspects of the golden ratio.
- Take notes on the mathematical concepts and formulas related to the golden ratio.
Solve problems involving Fibonacci numbers and the Golden ratio
Show steps
Reinforce your problem-solving skills by tackling challenges that involve applying Fibonacci numbers and the Golden ratio, improving your proficiency.
Browse courses on
Fibonacci Numbers
Show steps
- Find practice problems online or in textbooks.
- Set aside dedicated time for solving the problems.
- Check your solutions against provided answers or work with a tutor to verify your understanding.
Explore interactive visualizations of the Golden ratio
Show steps
Delve deeper into the Golden ratio through interactive visualizations, enhancing your comprehension of its properties and applications.
Show steps
- Locate interactive visualizations of the Golden ratio online.
- Explore the visualizations, observing how the Golden ratio manifests in various geometric forms.
Fibonacci Formula Practice
Show steps
Apply your knowledge of the Fibonacci Formula by completing a series of practice problems.
Browse courses on
Fibonacci Numbers
Show steps
- Review the Fibonacci Formula: F(n) = F(n-1) + F(n-2)
- Solve practice problems involving the Fibonacci Formula
- Check your answers and identify areas for improvement
Fibonacci Problem-Solving Collaboration
Show steps
Engage in peer discussions and problem-solving sessions to deepen your understanding of Fibonacci-related concepts.
Browse courses on
Fibonacci Numbers
Show steps
- Join or form a study group with other students
- Discuss complex Fibonacci problems and share different approaches
- Collaborate on solving challenging problems and provide constructive feedback
Golden Ratio in Nature
Show steps
Explore the fascinating applications of the Golden Ratio in nature, from the spiral patterns of seashells to the arrangement of leaves on a plant stem.
Show steps
- Research the Golden Ratio and its significance in nature
- Identify examples of the Golden Ratio in various natural phenomena
- Analyze how the Golden Ratio contributes to the aesthetics and functionality of natural structures
Write a blog post about the applications of Fibonacci numbers
Show steps
Write a blog post to demonstrate your understanding of the applications of Fibonacci numbers in various fields, such as nature, art, and architecture.
Browse courses on
Applications
Show steps
- Research the applications of Fibonacci numbers
- Write a blog post outlining your findings
Create a visual representation of the Fibonacci spiral
Show steps
Solidify your understanding of the Fibonacci spiral by creating your own visual representation, fostering a deeper connection with the concept.
Show steps
- Choose a method for creating your visual representation (e.g., drawing, digital art, physical model).
- Plan the layout and incorporate the Fibonacci spiral into your design.
- Execute your design, accurately representing the proportions and patterns of the Fibonacci spiral.
Fibonacci Sequence in Music
Show steps
Demonstrate your understanding of the Fibonacci Sequence by creating a piece of music that incorporates its principles.
Browse courses on
Fibonacci Numbers
Show steps
- Study the Fibonacci Sequence and its mathematical properties
- Compose a musical piece using the Fibonacci Sequence as a guide for note durations, rhythms, or melodic patterns
- Share your musical composition with others for feedback and appreciation
Fibonacci Challenge
Show steps
Test your skills and knowledge by participating in a Fibonacci-themed competition or challenge.
Browse courses on
Fibonacci Numbers
Show steps
- Identify and register for a suitable Fibonacci competition or challenge
- Prepare thoroughly by studying Fibonacci-related concepts and practicing problem-solving
- Compete in the challenge and strive for excellence
- Reflect on your performance and identify areas for improvement
Career center
Mathematician
Physics Teacher
Math Teacher
Computer Science Teacher
Quantitative Analyst
Actuary
Software Developer
Operations Research Analyst
Statistician
Financial Analyst
Risk Analyst
Investment Analyst
Computer Scientist
Data Analyst
Market Researcher
Reading list
Share
Similar courses
OpenCourser helps millions of learners each year. People visit us to learn workspace skills, ace their exams, and nurture their curiosity.
Our extensive catalog contains over 50,000 courses and twice as many books. Browse by search, by topic, or even by career interests. We'll match you to the right resources quickly.
Find this site helpful? Tell a friend about us.
We're supported by our community of learners. When you purchase or subscribe to courses and programs or purchase books, we may earn a commission from our partners.
Your purchases help us maintain our catalog and keep our servers humming without ads.
Thank you for supporting OpenCourser.



