Sensitivity Analysis: Understanding How Variables Impact Outcomes

Sensitivity analysis is a powerful technique used to determine how different values of an independent variable affect a dependent variable under a specific set of assumptions. Essentially, it helps us understand how much an outcome changes when we tweak the inputs of a model or system. This "what-if" analysis, as it's often called, is crucial for making informed decisions and managing risk in a wide array of fields.

Working with sensitivity analysis can be quite engaging. Imagine being able to peer into the potential futures of a project or investment by systematically exploring different scenarios. It allows for a proactive approach to change, providing the information needed to make adjustments before unintended consequences arise. Furthermore, sensitivity analysis adds a layer of credibility to any model by testing its robustness across a spectrum of possibilities, helping to identify which factors have the most significant impact on the results. This ability to pinpoint critical variables can be incredibly exciting as it empowers individuals and organizations to focus their efforts where they matter most.

Introduction to Sensitivity Analysis

Sensitivity analysis is a cornerstone of robust decision-making in a world filled with uncertainty. It provides a systematic way to explore how the output of a model or system responds to changes in its input parameters. This process is vital for anyone who relies on models to make predictions, understand complex systems, or assess risks.

Definition and Core Purpose of Sensitivity Analysis

At its core, sensitivity analysis is the study of how the uncertainty in the output of a mathematical model or system can be apportioned to different sources of uncertainty in its inputs. Its primary purpose is to identify which input variables have the most significant impact on the model's output. By understanding these relationships, analysts can gain insights into the model's behavior, test the robustness of its results, and identify areas where more precise data or further investigation is needed.

This technique helps in making more informed decisions by quantifying how sensitive an outcome is to changes in underlying assumptions. For example, a business might use sensitivity analysis to understand how changes in material costs, labor rates, or market demand could affect the profitability of a new product. By systematically varying these inputs, they can identify the key drivers of profitability and develop strategies to mitigate potential risks.

Sensitivity analysis is not just about identifying problems; it's also about uncovering opportunities. By understanding which variables have the most leverage, decision-makers can focus on optimizing those factors to achieve better outcomes. It brings a level of rigor and transparency to the decision-making process, allowing for a clearer understanding of the potential range of outcomes and the factors that drive them.

Historical Context and Evolution of the Concept

The foundational ideas behind sensitivity analysis can be traced back to the 17th century with the development of probability theory by mathematicians like Pierre de Fermat and Blaise Pascal. Their work on games of chance provided a way to quantify uncertainty and understand how variables affect outcomes, which are central concepts in sensitivity analysis.

The more formal application of sensitivity analysis gained traction during World War II, where it proved useful for strategic decision-making. As computational power grew, its use expanded into other fields such as engineering, finance, and environmental modeling. In the 1970s, mathematician Paul Cukier and his colleagues developed the Fourier Amplitude Sensitivity Test (FAST), a significant advancement that allowed for the analysis of multiple variables simultaneously, moving beyond the limitations of earlier one-at-a-time methods.

Over the decades, various methods and techniques have been developed, ranging from simple local approaches to more complex global methods. The evolution has been driven by the increasing complexity of models and the growing need for robust decision-making tools in diverse domains. Today, sensitivity analysis is an integral part of model building, quality assurance, and risk assessment across numerous disciplines.

Key Industries/Fields Where It Is Applied

Sensitivity analysis is a versatile tool with applications across a multitude of industries. In finance and economics, it's used extensively for financial modeling, investment risk assessment, and predicting the impact of economic variables. For instance, analysts might use it to see how changes in interest rates affect bond prices or how variations in sales forecasts impact a company's net present value.

Engineering is another major field where sensitivity analysis plays a critical role. Engineers use it to test the robustness of designs, assess the impact of manufacturing tolerances, and optimize performance. For example, in structural engineering, it can help determine how variations in material properties or load conditions might affect the safety and stability of a bridge.

In environmental science, sensitivity analysis is crucial for understanding complex environmental models, such as those used for climate change prediction or pollution control. It helps identify which parameters (e.g., emission rates, reaction kinetics) have the most influence on model outcomes, guiding research and policy decisions. Other fields that heavily rely on sensitivity analysis include healthcare and pharmaceutical research for evaluating treatment efficacy and drug development processes, as well as in business for strategic planning and operational improvements.

Why It Matters for Decision-Making and Risk Assessment

Sensitivity analysis is paramount for effective decision-making and robust risk assessment because it provides a clear understanding of how uncertainties in inputs can translate into variability in outcomes. By identifying the most influential variables—those that cause the most significant changes in the output when they are altered—decision-makers can focus their attention and resources on managing these critical factors. This allows for more targeted risk mitigation strategies.

Consider a company deciding whether to invest in a new project. A sensitivity analysis can reveal how changes in key assumptions, such as market growth rate or production costs, could impact the project's profitability. If the project's success is highly sensitive to a variable that is difficult to predict or control, the company might decide to gather more information, develop contingency plans, or even reconsider the investment. This systematic exploration of "what-if" scenarios helps to build more resilient plans and avoid costly surprises.

Furthermore, sensitivity analysis enhances the credibility and transparency of modeling efforts. By explicitly acknowledging and quantifying the impact of uncertainty, it provides a more realistic picture of potential outcomes compared to relying on single-point estimates. This fosters greater confidence in the decisions based on such models and facilitates better communication of risks and opportunities to stakeholders.

Key Concepts and Terminology

To fully grasp sensitivity analysis, it's helpful to understand some of its fundamental concepts and the language used to describe them. These building blocks will pave the way for a deeper exploration of its methods and applications.

Input vs. Output Variables

In the context of sensitivity analysis, a model or system is typically viewed as a process that transforms a set of input variables into one or more output variables. Input variables, also known as parameters or factors, are the elements that are fed into the model. These can be uncertain quantities, assumptions, or decision variables that can be changed or varied. For example, in a financial model projecting company profits, input variables might include sales volume, price per unit, cost of goods sold, and operating expenses.

Output variables, on the other hand, are the results or outcomes produced by the model based on the given inputs. In the company profit model, the output variable would be the projected profit. Sensitivity analysis examines how changes in the input variables (e.g., a 10% increase in sales volume or a 5% decrease in material costs) affect the output variable (profit). Understanding this relationship is the crux of the analysis.

The distinction between input and output variables is crucial for setting up a sensitivity analysis correctly. The goal is to systematically manipulate the inputs and observe the corresponding changes in the outputs to determine which inputs have the most significant influence.

Local vs. Global Sensitivity Analysis

Sensitivity analysis methods can be broadly categorized into local and global approaches. Local sensitivity analysis typically involves changing one input variable at a time (often referred to as One-at-a-Time or OAT) while keeping all other inputs fixed at their baseline or nominal values. The sensitivity is then assessed based on the rate of change or the partial derivative of the output with respect to that specific input variable around that nominal point. This approach is computationally less expensive and easier to implement, but its main limitation is that it only explores a small fraction of the input space and may not capture interactions between variables or non-linear responses accurately.

Global sensitivity analysis (GSA), in contrast, explores the entire range of possible values for each input variable and considers the simultaneous variation of multiple inputs. GSA methods aim to apportion the uncertainty in the model output to the uncertainty in the different input factors, taking into account interactions and non-linearities. Techniques like variance-based methods (e.g., Sobol indices) fall under this category. While more computationally intensive, GSA provides a more comprehensive and robust understanding of how input uncertainties affect the model output across the entire input space.

Choosing between local and global methods depends on the complexity of the model, the number of input variables, computational resources, and the specific goals of the analysis. For simple models or initial explorations, local methods might suffice. For complex, non-linear models where interactions are important, global methods are generally preferred.

Uncertainty Quantification

Uncertainty quantification (UQ) is a field closely related to sensitivity analysis; ideally, they are performed in tandem. While sensitivity analysis focuses on how much each input variable contributes to the output uncertainty, UQ aims to determine and characterize the uncertainty present in the model's inputs, parameters, and the model structure itself, and then to propagate this uncertainty through the model to understand the uncertainty in the output.

UQ involves identifying the sources of uncertainty, representing them mathematically (often using probability distributions), and then propagating these uncertainties through the model to obtain a probabilistic description of the model's output. This might involve techniques like Monte Carlo simulation, where the model is run many times with inputs sampled from their respective probability distributions. The result is often a probability distribution for the output, which can provide insights into the range of possible outcomes and their likelihoods.

Sensitivity analysis often follows uncertainty quantification. Once the overall output uncertainty is understood, sensitivity analysis helps to break down that uncertainty and attribute it to specific input uncertainties. This helps prioritize efforts to reduce uncertainty by focusing on the inputs that matter most. For those interested in building a foundational understanding, exploring resources on probability and statistics is a good starting point.

You may wish to explore these topics if uncertainty quantification interests you:

These books offer a deeper dive into the concepts of uncertainty and its quantification in modeling.

For those looking to get started with UQ, the following course provides an introduction.

Scenarios and Parameter Ranges

A crucial aspect of conducting sensitivity analysis involves defining realistic scenarios and appropriate parameter ranges for the input variables. Scenarios represent different plausible situations or sets of assumptions under which the model will be evaluated. For example, in a business context, one might define optimistic, pessimistic, and most likely scenarios for key market variables.

Parameter ranges define the lower and upper bounds within which each input variable will be varied during the analysis. Setting these ranges appropriately is critical; if they are too narrow, the analysis might underestimate the true sensitivity, and if they are too wide or unrealistic, the results might be misleading. These ranges are often determined based on historical data, expert judgment, literature review, or the inherent physical limits of the parameters.

The choice of scenarios and parameter ranges directly influences the outcomes and interpretations of the sensitivity analysis. It's important to clearly document these choices and the rationale behind them. In some forms of sensitivity analysis, like scenario analysis, specific combinations of input values representing different scenarios are directly evaluated. In other methods, like Monte Carlo simulation, input variables are sampled from probability distributions defined over their respective ranges.

The following courses touch upon scenario analysis in different contexts.

Applications in Different Industries

The principles of sensitivity analysis find practical application across a diverse array of industries, helping professionals make more informed decisions, manage risks, and optimize outcomes. Its ability to quantify the impact of changing variables makes it an invaluable tool in complex systems.

Financial Modeling and Investment Risk Assessment

In the realm of finance, sensitivity analysis is a cornerstone of financial modeling and investment risk assessment. Analysts build models to forecast company performance, value assets, or assess the viability of projects. Sensitivity analysis allows them to understand how dependent their conclusions are on key assumptions, such as sales growth rates, discount rates, or commodity prices. For example, when performing a Discounted Cash Flow (DCF) valuation, an analyst will almost certainly conduct a sensitivity analysis on the discount rate and growth rate assumptions to see how the valuation changes.

This process helps in identifying the most critical variables that could impact an investment's return or a company's financial health. By understanding these sensitivities, investors and financial managers can better gauge the riskiness of an investment, develop hedging strategies, or make more robust capital budgeting decisions. It helps answer crucial "what-if" questions, such as "What happens to our net present value if sales are 10% lower than expected?" or "How does a 1% increase in interest rates affect our bond portfolio's value?". This rigorous testing of assumptions leads to more resilient financial plans and strategies.

These courses provide practical insights into financial modeling and the application of sensitivity analysis in this domain.

For those looking for comprehensive texts on financial modeling and risk, these books are highly recommended.

You may also be interested in these related careers and topics:

Engineering Design Optimization

Engineering disciplines heavily rely on sensitivity analysis for design optimization and ensuring the reliability of systems. When designing structures, machines, or processes, engineers build mathematical or computational models to predict performance. Sensitivity analysis helps them understand how variations in design parameters (e.g., material properties, dimensions, operating conditions) affect key performance indicators (e.g., stress, efficiency, safety factors).

For instance, in aerospace engineering, sensitivity analysis can be used to determine how changes in an aircraft's wing shape or engine thrust affect its fuel efficiency or payload capacity. In chemical engineering, it can help optimize reactor conditions by identifying which temperature, pressure, or catalyst concentration settings have the most significant impact on product yield. By pinpointing the most influential parameters, engineers can focus their efforts on optimizing those specific aspects of the design, leading to more robust, efficient, and cost-effective solutions. It also plays a crucial role in tolerance analysis, helping to set acceptable manufacturing variations for components.

These courses delve into process modeling and optimization where sensitivity analysis is a key component.

Climate Modeling and Environmental Policy

In the fields of climate science and environmental policy, sensitivity analysis is indispensable for understanding the behavior of complex environmental models and for informing policy decisions. Climate models, for example, involve numerous interconnected parameters representing atmospheric, oceanic, and terrestrial processes. Sensitivity analysis helps scientists identify which of these parameters (e.g., greenhouse gas emission rates, cloud reflectivity, ocean heat uptake efficiency) exert the strongest influence on projections of future climate change.

This understanding is critical for several reasons. It can guide research efforts by highlighting areas where reducing uncertainty in parameter estimation would most improve model accuracy. It also helps policymakers understand the potential range of outcomes under different emission scenarios or policy interventions. For example, sensitivity analysis can be used to assess how different levels of carbon tax or investments in renewable energy might impact future temperature rise or sea-level change. This allows for more informed and robust environmental policymaking.

The following course looks at modeling carbon emissions, a key area in climate science.

This book provides a broad overview of environmental modeling.

Healthcare and Pharmaceutical Research

Sensitivity analysis plays a vital role in healthcare and pharmaceutical research, aiding in areas from epidemiological modeling to drug development and health technology assessment. In epidemiology, models are used to predict the spread of diseases, and sensitivity analysis can identify which factors (e.g., transmission rates, vaccination coverage, effectiveness of interventions) have the greatest impact on the epidemic's trajectory. This information is crucial for public health planning and resource allocation.

In pharmaceutical research, sensitivity analysis is used during drug development to understand how variations in dosage, patient characteristics, or metabolic rates might affect a drug's efficacy and safety. It is also a key component of Health Technology Assessment (HTA), where the cost-effectiveness of new medical treatments or interventions is evaluated. [rtwxim] Analysts use sensitivity analysis to explore how uncertainties in clinical effectiveness, costs, or patient utilities might change the conclusions about whether a new technology represents good value for money. This helps healthcare payers and providers make evidence-based decisions about adopting new treatments and technologies.

This course introduces concepts in Health Technology Assessment where sensitivity analysis is frequently applied.

For those interested in mathematical modeling in life sciences, this book may be of interest.

Methods and Techniques

A variety of methods and techniques have been developed for conducting sensitivity analysis, each with its own strengths, weaknesses, and areas of applicability. These methods range from simple, intuitive approaches to more mathematically sophisticated ones.

One-at-a-Time (OAT) Methods

One-at-a-Time (OAT) methods, also known as local sensitivity analysis, are among the simplest and most widely used techniques. The basic idea is to vary one input variable (or parameter) at a time, while holding all other input variables constant at their baseline or nominal values. The effect of this change on the model output is then observed. This process is repeated for each input variable of interest.

The sensitivity is often measured by calculating how much the output changes in response to a specific change in the input (e.g., a 10% increase) or by looking at the partial derivative of the output with respect to the input. OAT methods are computationally inexpensive and easy to understand and implement. However, their major limitation is that they do not account for interactions between input variables. If the effect of one variable depends on the level of another, OAT methods will not capture this. They also only explore the sensitivity around a single point (the baseline values) in the input space, which may not be representative if the model is highly non-linear.

Despite these limitations, OAT analysis can be a useful first step in understanding a model, particularly for identifying potentially influential parameters for further, more detailed investigation.

Monte Carlo Simulations

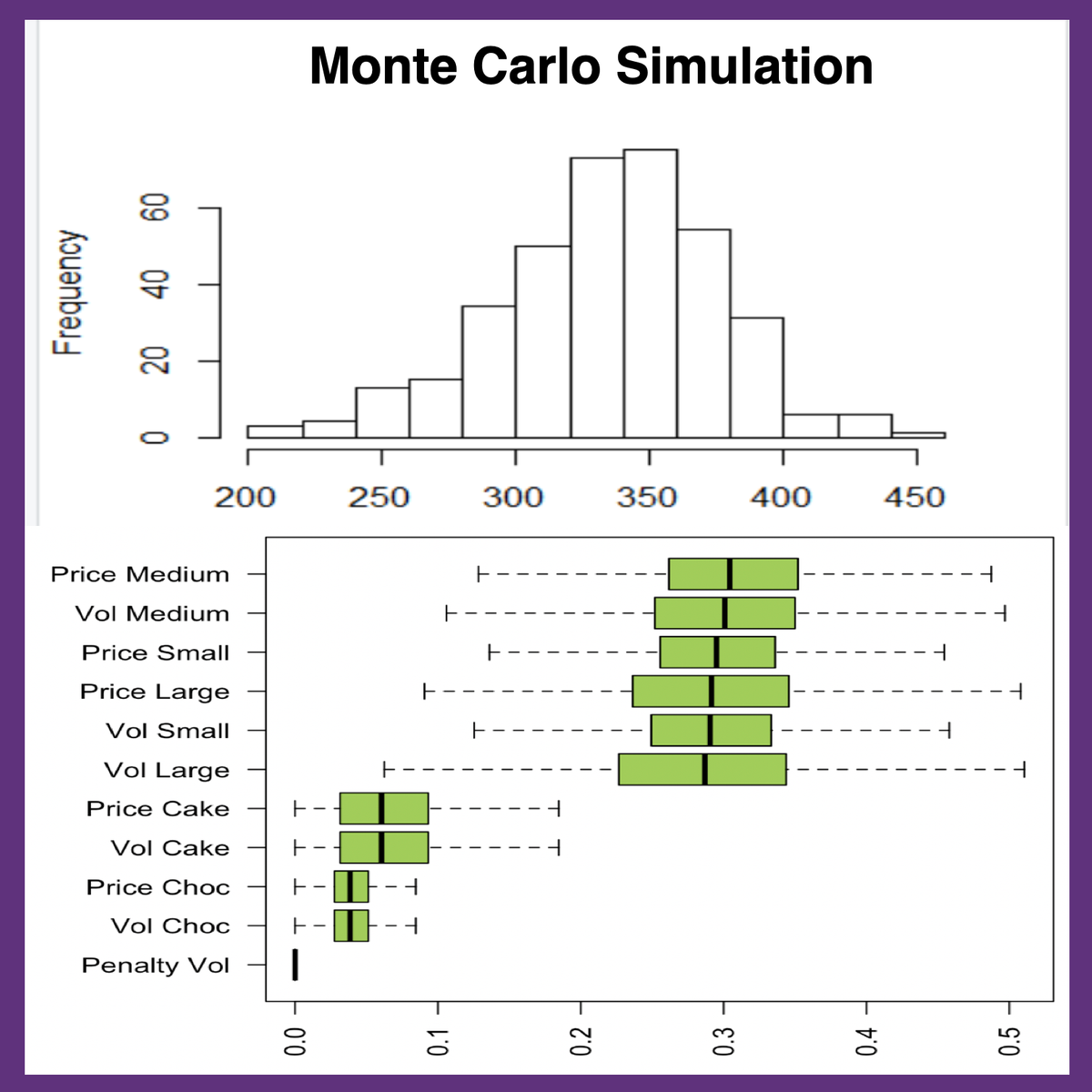
Monte Carlo simulation is a powerful and versatile technique often used for global sensitivity analysis. Instead of varying inputs one at a time, Monte Carlo methods involve repeatedly sampling values for all input variables simultaneously from their respective probability distributions (or defined ranges). The model is then run with each set of sampled input values, generating a distribution of output values.

By analyzing the relationship between the sampled inputs and the resulting outputs (often using statistical techniques like regression analysis or variance decomposition), one can determine the sensitivity of the output to each input variable across its entire range. Monte Carlo simulations can handle complex, non-linear models and can capture interactions between variables. The main drawback is that they can be computationally expensive, especially for models that take a long time to run or have a large number of input variables, as a large number of model evaluations (samples) are typically required to achieve accurate results.

Quasi-Monte Carlo methods, which use low-discrepancy sequences (like Sobol sequences) instead of purely random sampling, can often improve the efficiency of the estimation, requiring fewer samples for a given level of accuracy.

This course provides an application of Monte Carlo simulation in the context of Six Sigma.

This book discusses simulation experiments, which often involve Monte Carlo methods.

Variance-Based Techniques (e.g., Sobol Indices)

Variance-based techniques are a popular class of global sensitivity analysis methods that aim to apportion the variance in the model output to the variance in the input variables. The most well-known of these are Sobol indices, named after Ilya M. Sobol.

Sobol indices quantify the contribution of each input variable (or groups of variables) to the total variance of the model output. The "first-order Sobol index" for an input variable measures the direct contribution of that variable's variance to the output variance (i.e., its main effect). "Total-order Sobol indices" (or total effect indices) measure the main effect of a variable plus all its interaction effects with other variables. By comparing these indices, analysts can understand not only which variables are important individually but also the extent to which interactions between variables drive output uncertainty.

These methods are powerful because they provide a quantitative ranking of input importance, can handle non-linear and non-monotonic models, and explicitly account for interactions. However, they are typically computationally intensive as they often rely on Monte Carlo simulations to estimate the necessary variances and conditional variances. The interpretation of Sobol indices requires a good understanding of variance decomposition.

This book is a key reference for global sensitivity analysis, including variance-based methods.

Machine Learning Integration

More recently, there has been a growing trend towards integrating machine learning (ML) techniques with sensitivity analysis. ML models, such as random forests or neural networks, can be used to create "surrogate models" or "meta-models" that approximate the behavior of the original, more complex model. These surrogate models are typically much faster to evaluate, making it feasible to perform extensive global sensitivity analysis (like calculating Sobol indices) that would be computationally prohibitive with the original model.

Furthermore, some ML algorithms inherently provide measures of "feature importance," which can be interpreted as a form of sensitivity analysis. For example, techniques like SHAP (SHapley Additive exPlanations) or LIME (Local Interpretable Model-Agnostic Explanations) can help explain the predictions of complex ML models by quantifying the contribution of each input feature. AI-driven sensitivity analysis can also automate parts of the process, handle high-dimensional data more effectively, and potentially uncover complex, non-linear relationships that traditional methods might miss.

The integration of AI and ML holds significant promise for making sensitivity analysis more powerful, efficient, and accessible, especially for very complex systems and large datasets. This is an active area of research and development.

You may find these related topics interesting if you wish to explore the intersection of AI and analytics.

Tools and Software for Sensitivity Analysis

A variety of software tools are available to assist practitioners in performing sensitivity analysis, ranging from general-purpose programming languages with specialized libraries to dedicated commercial software packages. The choice of tool often depends on the complexity of the model, the specific sensitivity analysis methods to be used, the user's programming skills, and budget considerations.

Open-Source Tools (e.g., Python Libraries like SALib)

For those who prefer open-source solutions or need flexibility in integrating sensitivity analysis into larger computational workflows, several excellent tools are available. Python, with its extensive ecosystem of scientific computing libraries, is a popular choice. The SALib (Sensitivity Analysis Library in Python) is a widely used open-source library that provides implementations of various sensitivity analysis methods, including Sobol, Morris, and FAST. It allows users to easily generate input samples, run their models, and then analyze the results to compute sensitivity indices.

R, another powerful open-source language for statistical computing and graphics, also offers packages for sensitivity analysis. These tools provide the advantage of being free, highly customizable, and supported by active communities. They are particularly well-suited for researchers and practitioners who are comfortable with programming and want fine-grained control over the analysis process. Many of these libraries can be integrated with other data analysis and visualization tools, allowing for a comprehensive analytical pipeline.

Commercial Software (e.g., MATLAB, Simulink)

Several commercial software packages also offer robust capabilities for sensitivity analysis. MATLAB, along with its companion product Simulink for model-based design, provides toolboxes (such as Simulink Design Optimization) that include functions for performing both local and global sensitivity analysis. These tools are often used in engineering and scientific research, offering features for parameter estimation, optimization, and uncertainty quantification alongside sensitivity analysis.

Other commercial software in fields like risk analysis (e.g., @RISK, an add-in for Excel) or specialized simulation environments often incorporate sensitivity analysis modules. These tools typically provide user-friendly interfaces, integrated workflows, and sometimes advanced visualization options, which can be beneficial for users who prefer a graphical environment or need to perform complex analyses without extensive programming. The trade-off is generally the cost of the software licenses.

If you are interested in learning how to use MATLAB for these types of analyses, these resources may be helpful.

Criteria for Selecting Tools

Choosing the right tool for sensitivity analysis depends on several factors. Cost is often a primary consideration, with open-source tools being free while commercial packages can have significant licensing fees. Scalability is another important factor: can the tool handle the size and complexity of your model and the number of simulations required, especially for global sensitivity analysis methods? Some tools are better optimized for high-performance computing environments.

User-friendliness and the required learning curve are also key. Graphical user interfaces (GUIs) in commercial software might be easier for beginners, while command-line interfaces or programming libraries offer more flexibility for experienced users. The specific sensitivity analysis methods supported by the tool must align with your analytical needs. Some tools specialize in certain types of analysis (e.g., variance-based methods), while others offer a broader range.

Finally, consider the tool's ability to integrate with your existing modeling environment and data sources. If your model is already built in a specific software (like Simulink or Excel), using a tool that directly interfaces with it can save considerable effort. The availability of good documentation, tutorials, and community or vendor support can also be crucial.

Integration with Data Visualization Platforms

Effective communication of sensitivity analysis results is critical, and data visualization plays a key role in this. Many sensitivity analysis tools offer built-in plotting capabilities to help users understand and present their findings. Common visualizations include tornado plots (which rank input variables by their impact on the output), scatter plots (showing the relationship between individual inputs and the output), and bar charts of sensitivity indices.

For more advanced or customized visualizations, it's often beneficial to integrate the sensitivity analysis workflow with dedicated data visualization platforms or libraries. For example, results from Python-based sensitivity analysis can be easily visualized using libraries like Matplotlib, Seaborn, or Plotly. Similarly, data exported from commercial tools can often be imported into business intelligence platforms like Tableau or Power BI for creating interactive dashboards.

These visualizations help in identifying key sensitivities at a glance, understanding complex relationships, and communicating the implications of the analysis to both technical and non-technical audiences. The ability to clearly illustrate which inputs drive output variability is essential for translating analytical insights into actionable decisions.

Formal Education Pathways

For individuals aspiring to specialize in areas that heavily utilize sensitivity analysis, or for those who wish to incorporate it rigorously into their work, formal education can provide a strong theoretical and practical foundation. This often involves coursework in quantitative disciplines and can extend to advanced research.

Undergraduate Courses in Statistics or Operations Research

A solid grounding in mathematics, particularly statistics and probability, is fundamental for understanding and applying sensitivity analysis. Undergraduate programs in statistics, mathematics, economics, engineering, computer science, or operations research often include courses that cover the foundational concepts. Look for courses that delve into regression analysis, experimental design, probability distributions, and Monte Carlo methods, as these are all relevant to various sensitivity analysis techniques.

Operations research courses, in particular, often focus on modeling and optimization, where sensitivity analysis plays a key role in understanding the robustness of solutions and the impact of changing parameters. [k6l6u6] While specific undergraduate courses solely dedicated to "Sensitivity Analysis" might be rare, the principles are often embedded within these broader quantitative subjects. Building a strong analytical and quantitative skillset at the undergraduate level is crucial.

These courses offer an introduction to operations research and spreadsheet modeling, which are relevant foundational areas.

Exploring these related topics can also be beneficial:

Graduate Programs Emphasizing Quantitative Analysis

Graduate programs (Master's or PhD) in fields like data science, statistics, operations research, financial engineering, econometrics, computational science, or specific engineering disciplines often offer more specialized training in sensitivity analysis and related areas like uncertainty quantification. [ds0uky] These programs typically involve more advanced coursework in mathematical modeling, simulation, and advanced statistical methods.

Students in such programs are likely to encounter sensitivity analysis in the context of their research projects or thesis work, applying it to complex problems in their respective domains. For example, a PhD student in environmental engineering might use global sensitivity analysis to understand the key drivers of uncertainty in a water quality model. A Master's student in finance might use it to assess the risk of complex derivatives. These advanced programs provide the depth of knowledge required to develop and apply sophisticated sensitivity analysis techniques.

This course provides a more advanced look at analytics relevant to graduate-level study.

PhD Research Areas

For those pursuing doctoral studies, sensitivity analysis can be a significant component of research across many disciplines that rely on computational modeling. PhD research might focus on developing new sensitivity analysis methodologies, improving the computational efficiency of existing methods, or applying these techniques to novel and complex problems. For example, research areas could include developing sensitivity analysis methods for high-dimensional models, for models with dependent inputs, or for coupled multi-physics simulations.

Specific PhD research areas where sensitivity analysis is prominent include computational engineering (e.g., fluid dynamics, structural mechanics), climate modeling, systems biology, financial mathematics, and uncertainty quantification. Researchers in these fields often publish their work in specialized journals and present at conferences dedicated to modeling, simulation, and computational science. A PhD focusing on or heavily utilizing sensitivity analysis can lead to careers in academia, research institutions, or advanced R&D roles in industry.

Certifications and Workshops

While formal degrees provide comprehensive education, certifications and specialized workshops can offer more focused training on sensitivity analysis tools and techniques. Some professional organizations or software vendors may offer certifications related to risk management, financial modeling, or specific simulation software, which might include components on sensitivity analysis.

Workshops, often offered by universities, research Ccnters, or at scientific conferences, can provide intensive, hands-on training on particular sensitivity analysis methods or software tools (like SALib in Python or MATLAB's toolboxes). These shorter-format learning opportunities can be valuable for professionals looking to acquire specific skills or stay updated on the latest developments without committing to a full degree program. They can also be a good way for students to supplement their formal education. Searching for workshops related to "uncertainty quantification," "computational modeling," or "risk analysis" might yield relevant results.

Consider these courses which cover risk analysis, a field closely tied to sensitivity analysis and often part of certification pathways.

Online Learning and Self-Study

For individuals seeking to learn about sensitivity analysis outside of traditional academic programs, or for professionals aiming to upskill, online learning and self-study offer flexible and accessible pathways. A wealth of resources is available, from structured courses to project-based learning opportunities.

Online courses are highly suitable for building a foundational understanding of sensitivity analysis. Many platforms offer courses in statistics, data analysis, financial modeling, and programming languages like Python or R, all of which are relevant. These courses often break down complex topics into digestible modules, include practical exercises, and sometimes offer certificates upon completion. Learners can use OpenCourser to search through thousands of online courses and find options that fit their learning goals and current skill level. The "Save to list" feature on OpenCourser can be particularly helpful for shortlisting promising courses for later review.

Structured Learning Paths for Beginners

For beginners, starting with foundational concepts is key. A structured learning path might begin with introductory statistics and probability courses to understand concepts like variables, distributions, variance, and correlation. [j3zpa6] This could be followed by courses on basic data analysis and spreadsheet modeling, perhaps using Excel, to get comfortable with manipulating data and building simple models. [ik17ns, y0o3qs]

Once these fundamentals are in place, learners can move on to courses that introduce financial modeling (if interested in finance applications) or basic programming in Python or R, which are essential for using more advanced sensitivity analysis libraries. [m82fg7] Look for courses that explicitly mention "sensitivity analysis," "what-if analysis," or "scenario analysis" in their syllabus. [j5yhgo, cdfgq5] Some courses might focus on specific application areas, such as engineering or environmental science, which can be beneficial if you have a particular field of interest. OpenCourser's Learner's Guide offers articles on how to create a structured curriculum for yourself, which can be invaluable for self-learners.

These courses are excellent starting points for beginners interested in financial modeling and spreadsheet-based analysis, which often incorporate sensitivity analysis.

This book offers a good introduction to financial modeling with Excel.

Project-Based Learning to Apply Theoretical Knowledge

Theoretical knowledge becomes much more ingrained when applied to practical problems. Project-based learning is an excellent way to solidify your understanding of sensitivity analysis. After taking some foundational courses, try to find or devise small projects where you can apply what you've learned. This could involve building a simple financial model for a hypothetical business and then performing sensitivity analysis on key assumptions like sales price or costs.

If you're learning programming, you could try to replicate examples from sensitivity analysis tutorials using libraries like SALib in Python. Many online courses, especially on platforms like Coursera or edX, incorporate projects into their curriculum. [7k8q2e] For example, a course on data analysis might have a project where you analyze a dataset and use sensitivity techniques to understand the impact of different variables on an outcome. The "Activities" section on OpenCourser course pages often suggests projects or exercises that can supplement coursework, helping to deepen understanding and practical skills.

This project-based course allows learners to apply Monte Carlo simulation and sensitivity analysis using RStudio.

Combining Free and Paid Resources Effectively

A wealth of both free and paid resources is available for learning sensitivity analysis. Free resources include open-courseware from universities (e.g., MIT OpenCourseware), tutorials on programming websites, documentation for open-source libraries like SALib, and academic papers or pre-prints (e.g., on arXiv.org). YouTube channels dedicated to data science, finance, or engineering often have introductory videos on the topic.

Paid resources include structured online courses on platforms like Coursera, Udemy, or edX, which often offer more comprehensive content, instructor support, and certificates. Textbooks on financial modeling, risk analysis, or specific simulation techniques are also valuable paid resources. [kklp77, yyv6z2] An effective strategy is to start with free resources to get an overview and identify areas of interest, then invest in paid courses or books for more in-depth learning or specialized topics. OpenCourser's deals page can help learners find discounts on online courses and books.

These books are excellent resources for a deeper dive into sensitivity analysis and related topics.

Portfolio Development for Career Transitions

If you're aiming to transition into a career that utilizes sensitivity analysis (e.g., data analyst, financial analyst, risk analyst), building a portfolio of projects is crucial. [glc9ct, mxc3wi, 4161ts] This portfolio showcases your practical skills and your ability to apply theoretical knowledge to real-world (or realistic) problems. Include projects where you've clearly defined a problem, built a model, performed sensitivity analysis, and interpreted the results.

Document your projects thoroughly. Explain the objective, the methods used (including the specific sensitivity analysis techniques), the tools (e.g., Excel, Python with SALib), and the insights gained. If possible, use publicly available datasets or create well-documented hypothetical scenarios. You can host your projects on platforms like GitHub (for code-based projects) or create a personal website or blog to present your work. OpenCourser's features like "Save to List" can be used to curate a list of courses and projects you've completed, which can then be shared. Ensure your OpenCourser profile is up-to-date to enhance visibility.

For those new to the field, this can feel daunting, but starting with small, manageable projects and gradually tackling more complex ones is a good approach. Each completed project is a step towards building a compelling portfolio and demonstrating your capabilities to potential employers.

Career Opportunities and Progression

Proficiency in sensitivity analysis can open doors to a variety of career opportunities across diverse industries. It is often a key skill for roles that involve modeling, forecasting, risk assessment, and data-driven decision-making. The career progression can range from entry-level analytical positions to specialized modeling roles and leadership positions within analytics teams.

Entry-Level Roles (e.g., Data Analyst, Risk Analyst)

For individuals starting their careers, roles such as Data Analyst, Junior Financial Analyst, or Risk Analyst often require skills in sensitivity analysis. [glc9ct, mxc3wi, 4161ts] In these positions, you might be responsible for building and maintaining models (e.g., financial forecasts, market models, risk assessment tools), performing "what-if" scenarios, and communicating the results to stakeholders. For example, a Data Analyst might use sensitivity analysis to understand how changes in marketing spend affect customer acquisition, while a Risk Analyst in a bank might use it to assess the impact of interest rate fluctuations on a loan portfolio. [glc9ct]

These entry-level roles typically require a bachelor's degree in a quantitative field like finance, economics, statistics, mathematics, engineering, or computer science. Strong analytical skills, proficiency in tools like Excel, and increasingly, knowledge of programming languages like Python or R, are highly valued. Demonstrating an understanding of modeling principles and the ability to interpret and communicate analytical results are key for success.

If you are exploring entry-level roles, consider these career paths and related analytical topics:

Mid-Career Specializations (e.g., Quantitative Modeler)

As professionals gain experience, they may move into more specialized mid-career roles such as Quantitative Modeler, Senior Financial Analyst, or Operations Research Analyst. [mxc3wi, epuo6h] These roles often involve developing and validating more complex models, applying advanced sensitivity analysis techniques (like global, variance-based methods), and providing deeper insights into model behavior and risk. For instance, a Quantitative Modeler in an investment bank might develop sophisticated models for pricing exotic derivatives and use sensitivity analysis to understand their risk profiles. An Operations Research Analyst might use it to optimize supply chains or production processes, assessing the sensitivity of optimal solutions to changes in costs or constraints. [epuo6h]

These roles typically require a Master's degree or even a PhD in a highly quantitative field, along with several years of practical experience in modeling and analysis. Expertise in specific software tools (e.g., MATLAB, specialized simulation packages) and programming languages is usually essential. Strong problem-solving skills and the ability to translate complex analytical findings into business implications are critical. The Bureau of Labor Statistics projects growth in fields like financial analysis and operations research analysis, indicating ongoing demand for these skills. For example, employment for financial analysts is projected to grow, and for operations research analysts, the growth is also projected to be faster than average.

For those considering mid-career specializations, these roles and topics are relevant:

Leadership Roles in Analytics Teams

With significant experience and a proven track record, individuals skilled in sensitivity analysis and broader quantitative modeling can advance to leadership roles within analytics teams. These might include positions like Analytics Manager, Director of Quantitative Research, or Chief Risk Officer. In these roles, the focus shifts from performing the analysis directly to overseeing teams of analysts, setting analytical strategy, ensuring the quality and robustness of models, and communicating key findings and recommendations to senior management or clients.

Leadership in analytics requires not only deep technical expertise but also strong management, communication, and strategic thinking skills. The ability to bridge the gap between complex technical analysis and business decision-making is paramount. These leaders play a crucial role in embedding data-driven and risk-aware decision-making processes within their organizations. They are responsible for ensuring that analytical capabilities are aligned with business objectives and that insights from models, including sensitivity analyses, are effectively used to drive performance and manage risk.

Freelancing and Consulting Opportunities

Experienced practitioners of sensitivity analysis can also find opportunities in freelancing or consulting. [r6hk5f] Many businesses, particularly small and medium-sized enterprises, may not have in-house expertise in advanced modeling and risk analysis but may require these skills for specific projects, such as valuing a potential acquisition, assessing the risk of a new venture, or optimizing their operations.

Consultants with expertise in sensitivity analysis can offer valuable services in these areas, helping clients build models, understand their sensitivities, and make more informed decisions. [r6hk5f] This path requires not only strong analytical skills but also entrepreneurial drive, good communication and client management skills, and the ability to market one's services effectively. Success in consulting often comes from developing a niche expertise in a particular industry (e.g., energy, finance, healthcare) or a specific type of modeling.

This career path might be of interest if you have substantial experience and are looking for flexible work arrangements.

Challenges and Limitations in Sensitivity Analysis

While sensitivity analysis is a powerful and widely applicable tool, it's not without its challenges and limitations. Understanding these can help practitioners apply the technique more effectively and interpret its results with appropriate caution.

Computational Complexity in High-Dimensional Systems

One of the significant challenges, particularly for global sensitivity analysis methods, is computational complexity, especially when dealing with models that have a large number of input variables (high-dimensional systems) or models that are themselves computationally expensive to run. Many global methods, like variance-based techniques, require a large number of model evaluations (often thousands or tens of thousands) to achieve stable and accurate sensitivity indices.

If a single run of the model takes hours or even days, performing such a large number of runs can become prohibitively time-consuming and resource-intensive. While techniques like surrogate modeling (using simpler, faster approximations of the complex model) or more efficient sampling strategies (like quasi-Monte Carlo) can help mitigate this, computational cost remains a practical barrier in many real-world applications. Researchers are continuously working on developing more efficient algorithms to tackle this challenge.

Assumptions Impacting Model Validity

The results of a sensitivity analysis are inherently tied to the underlying model and the assumptions made in constructing that model. If the model itself is a poor representation of reality, or if the assumptions about input variable ranges and distributions are incorrect, then the sensitivity analysis, no matter how rigorously performed, may produce misleading or irrelevant results.

For example, if a financial model omits a critical risk factor, the sensitivity analysis will not be able to assess the impact of that factor. Similarly, if the assumed range for an input variable is too narrow and doesn't capture its true potential variability, the analysis might underestimate its importance. It is crucial to invest effort in building a valid and credible model first, and to critically evaluate all assumptions before and during the sensitivity analysis process. The adage "garbage in, garbage out" applies just as much to sensitivity analysis as it does to modeling in general.

Interpreting Results for Non-Technical Stakeholders

Communicating the results of a sensitivity analysis, especially from more complex global methods, to non-technical stakeholders can be a significant challenge. Concepts like variance decomposition or Sobol indices might be difficult for decision-makers without a strong quantitative background to grasp. Presenting results in an intuitive and actionable way is crucial for the analysis to have an impact.

Analysts need to be skilled in translating complex statistical outputs into clear business implications. Visualizations like tornado charts or simple "what-if" scenario tables can be more effective than detailed statistical tables. Focusing on the key insights – which variables matter most, what are the plausible ranges of outcomes, and what are the key uncertainties – is more important than detailing every nuance of the methodology. Effective communication often requires understanding the audience's perspective and tailoring the presentation accordingly.

Balancing Accuracy with Resource Constraints

There is often a trade-off between the desired accuracy and comprehensiveness of a sensitivity analysis and the available resources (time, budget, computational power). Global sensitivity analysis methods that provide a more complete picture of sensitivities are generally more resource-intensive than simpler local methods.

Practitioners must make pragmatic choices about which methods to use and how extensively to explore the input space, given the constraints they face. Sometimes, a simpler, less accurate analysis performed quickly may be more valuable for timely decision-making than a highly sophisticated analysis that arrives too late. It's about finding the right balance – conducting an analysis that is rigorous enough to be credible and useful, yet feasible within the given resource limitations. This often involves an iterative approach, perhaps starting with simpler methods to identify key areas and then focusing more intensive efforts where they are most warranted. Careful planning and clear objectives are essential to make these trade-offs effectively.

Emerging Trends and Future Directions

The field of sensitivity analysis is continuously evolving, driven by advances in computational power, data availability, and analytical methodologies. Several emerging trends are shaping its future, promising more powerful, efficient, and widely applicable techniques.

AI-Driven Sensitivity Analysis

The integration of Artificial Intelligence (AI) and Machine Learning (ML) is a significant trend in sensitivity analysis. As mentioned earlier, ML models can serve as fast surrogates for complex simulations, enabling more extensive global sensitivity studies. Moreover, AI algorithms are being developed to automate aspects of the sensitivity analysis process itself, from identifying key variables to interpreting complex interactions.

Techniques like interpretable AI (e.g., SHAP, LIME) are providing new ways to understand the sensitivity of "black-box" ML models, which is crucial as these models become more prevalent in decision-making. AI can also help in analyzing vast datasets to uncover subtle sensitivities and patterns that might be missed by traditional approaches. The ongoing development in AI is expected to lead to more adaptive, real-time, and insightful sensitivity analysis tools. For further exploration, you might want to browse topics under Artificial Intelligence.

This book explores the broader topic of predictive analytics, which often incorporates AI and sensitivity analysis.

Real-Time Sensitivity in Dynamic Systems

Many real-world systems are dynamic, meaning their behavior and sensitivities change over time. Traditional sensitivity analysis often provides a static snapshot. However, there's a growing interest in developing methods for real-time sensitivity analysis in dynamic systems. This would allow for continuous monitoring of how sensitivities are evolving as new data comes in or as system conditions change.

Imagine, for example, a financial trading system where the sensitivity of a portfolio to different market factors could be updated in real-time, enabling faster and more adaptive risk management. Or in an industrial process, real-time sensitivity analysis could help operators adjust control parameters dynamically to maintain optimal performance as feedstock quality or environmental conditions fluctuate. Achieving this requires computationally efficient algorithms and integration with real-time data streams, presenting both challenges and exciting opportunities for innovation.

Cross-Disciplinary Applications

While sensitivity analysis is well-established in fields like finance and engineering, its application is expanding into new and diverse cross-disciplinary areas. For example, there's growing interest in using sensitivity analysis to understand the ethical implications of AI algorithms – for instance, to assess how sensitive an algorithm's output is to biases in the training data. This falls under the umbrella of AI ethics and responsible AI.

Other emerging application areas include social sciences, for understanding the dynamics of social systems; healthcare, for personalizing medicine by understanding individual patient sensitivities to treatments; and sustainability, for assessing the impact of different policies on complex socio-ecological systems. As models become more prevalent in all areas of research and decision-making, the need for robust sensitivity analysis to understand and validate these models will only grow. This cross-pollination of ideas and techniques across disciplines is likely to lead to novel methods and applications.

Open-Source Collaboration and Reproducibility

The push towards open science and reproducibility is also influencing the field of sensitivity analysis. There is an increasing emphasis on using open-source tools and platforms, sharing code and data, and ensuring that sensitivity analysis studies are conducted and reported in a transparent and reproducible manner. Libraries like SALib in Python are a testament to this trend, providing freely available, community-developed tools.

This collaborative approach accelerates innovation by allowing researchers to build upon each other's work, validate methods, and develop best practices. It also enhances the credibility and trustworthiness of sensitivity analysis results. Initiatives promoting FAIR data principles (Findable, Accessible, Interoperable, Reusable) and open modeling practices will further support this trend, making sensitivity analysis more robust and accessible to a wider community of users. The World Economic Forum often discusses the importance of open collaboration in technological advancement.

Frequently Asked Questions (Career Focus)

For those considering a career path that involves sensitivity analysis, or looking to incorporate it as a skill, several common questions arise. Addressing these can help provide clarity and set realistic expectations.

Is sensitivity analysis a standalone career or a supplementary skill?

For the vast majority of professionals, sensitivity analysis is a supplementary skill rather than a standalone career. It's a powerful tool used by data analysts, financial analysts, engineers, economists, operations research analysts, risk managers, and many other quantitative roles to enhance their primary job functions. [glc9ct, mxc3wi, w1jrnm, 7ln0xv, epuo6h, 4161ts] For example, a financial analyst doesn't just "do sensitivity analysis"; they use it as part of their broader work in financial modeling, valuation, and investment analysis. [mxc3wi]

However, in some highly specialized research or consulting roles, particularly those focused on developing new sensitivity analysis methodologies or applying them to extremely complex, cutting-edge problems (e.g., in advanced scientific computing or quantitative finance), one might find a career that is very heavily centered on this specific area. But typically, it's a critical component of a broader analytical or modeling toolkit.

What industries hire the most sensitivity analysis professionals?

Professionals who use sensitivity analysis are in demand across a wide range of industries. The financial services sector (including banking, investment management, insurance) is a major employer, as sensitivity analysis is integral to risk management, valuation, and financial forecasting. The engineering disciplines (aerospace, mechanical, civil, chemical, etc.) also heavily rely on it for design optimization, reliability analysis, and process control.

Other significant industries include consulting (management, financial, and technical consulting firms often seek these skills), energy (for modeling energy systems, markets, and environmental impacts), pharmaceuticals and healthcare (for drug development, clinical trial analysis, and health economics), and government and research institutions (for policy analysis, economic modeling, and scientific research). [3, 7, 9, 16, r6hk5f] Essentially, any industry that relies on complex modeling and data-driven decision-making will have a need for individuals skilled in sensitivity analysis.

How do I transition into this field from a non-technical background?

Transitioning into a field that uses sensitivity analysis from a non-technical background is challenging but achievable with a dedicated effort. The first step is to build a strong foundational understanding of quantitative concepts. This involves learning basic statistics, probability, and mathematics. Online courses can be an excellent starting point for this. Mathematics and Data Science categories on OpenCourser list many relevant introductory courses.

Next, acquire skills in relevant software tools. Proficiency in Excel is often a good first step, followed by learning a programming language like Python or R and associated data analysis/sensitivity analysis libraries (e.g., Pandas, NumPy, SALib). [m82fg7] Work on practical projects, even small ones, to apply your learning and build a portfolio. Consider pursuing certifications or a relevant Master's degree if a more formal qualification is needed for your target roles. Networking with professionals in your desired field and seeking mentorship can also be invaluable. It's a journey that requires persistence and a genuine interest in quantitative analysis, but the skills gained are highly transferable and in demand.

What soft skills complement technical expertise in this area?

While technical expertise is crucial, several soft skills are equally important for success in roles involving sensitivity analysis. Problem-solving is paramount – the ability to understand a complex problem, formulate it in a way that can be modeled, and then use sensitivity analysis to derive insights. Analytical and critical thinking skills are needed to design the analysis appropriately, interpret the results correctly, and understand the limitations.

Communication skills are vital for explaining complex methodologies and findings to diverse audiences, including non-technical stakeholders. This includes both written communication (e.g., reports, documentation) and verbal presentations. Attention to detail is critical, as small errors in model setup or parameter definition can lead to incorrect conclusions. Finally, curiosity and a desire for continuous learning are important, as the field and its tools are constantly evolving.

Are certifications necessary for employment?

Certifications are generally not strictly necessary for employment in roles that use sensitivity analysis, especially if you have a relevant degree and strong practical skills demonstrated through projects or experience. However, they can be beneficial in certain situations. For example, in finance, certifications like the CFA (Chartered Financial Analyst) or FRM (Financial Risk Manager) are highly regarded and cover aspects of quantitative analysis, including sensitivity analysis.

In some specialized software-driven roles, a certification in a particular modeling or simulation tool might be advantageous. For career changers or those with less traditional backgrounds, a relevant certification (e.g., in data analytics or a specific programming language) can help demonstrate commitment and a certain level of proficiency. Ultimately, employers are most interested in your ability to apply the skills effectively, so a strong portfolio of work and the ability to articulate your understanding during interviews often carry more weight than certifications alone. If you are considering certifications, OpenCourser's Learner's Guide has articles that discuss how to evaluate and leverage certifications.

How does automation impact job prospects in sensitivity analysis?

Automation, including AI and machine learning, is undoubtedly changing the landscape of many analytical fields, including sensitivity analysis. Some routine aspects of setting up and running sensitivity analyses may become more automated, potentially reducing the manual effort involved. However, this doesn't necessarily mean reduced job prospects for skilled professionals.

Instead, automation is more likely to shift the focus of human roles towards higher-value activities. This includes defining the problem and the objectives of the analysis, building and validating the underlying models, critically interpreting the results from automated tools, understanding the limitations and assumptions, and communicating the insights to drive decision-making. The demand for individuals who can bridge the gap between complex models and practical business or scientific applications, and who can ask the right questions, is likely to remain strong. Automation can free up analysts from tedious computations, allowing them to concentrate on more strategic and interpretive tasks. According to reports like the Future of Jobs Report by the World Economic Forum, analytical thinking and technological literacy are increasingly important skills.

Sensitivity analysis is a vital tool for anyone involved in modeling, forecasting, and decision-making under uncertainty. While it presents certain challenges, its ability to provide deep insights into the behavior of complex systems makes it an indispensable skill in today's data-driven world. Whether you are a student exploring career options, a professional looking to upskill, or a researcher tackling complex problems, understanding and applying sensitivity analysis can significantly enhance your ability to make robust, informed decisions.