Binary Search Trees
ploring Binary Search Trees: A Foundational Data Structure
A Binary Search Tree (BST) is a fundamental data structure in computer science used for organizing and managing sorted data. At its core, a BST is a node-based binary tree where each node has a comparable key (and an associated value, if any), and it satisfies the binary search property: the key in any node is greater than or equal to any key stored in its left subtree and less than or equal to any key stored in its right subtree. This ordered structure allows for efficient searching, insertion, and deletion of data. For those new to data structures, think of it as an organized filing system where finding a specific file is much faster than rummaging through a disorganized pile.
Working with Binary Search Trees can be quite engaging. The logical nature of their construction and manipulation offers a satisfying challenge, akin to solving a well-designed puzzle. Furthermore, understanding BSTs opens the door to comprehending more complex data structures and algorithms, forming a crucial building block in a computer science education. The efficiency gains BSTs provide in real-world applications, such as speeding up database queries or enabling quick lookups in large datasets, highlight their practical importance and can be a source of excitement for those who enjoy optimizing processes and improving performance.
Core Concepts and Terminology
To fully appreciate Binary Search Trees, it's important to become familiar with their underlying concepts and the language used to describe them. This knowledge will serve as a solid foundation for anyone looking to delve deeper into data structures and algorithms, whether for academic pursuits or professional development.
Node Structure and Pointers
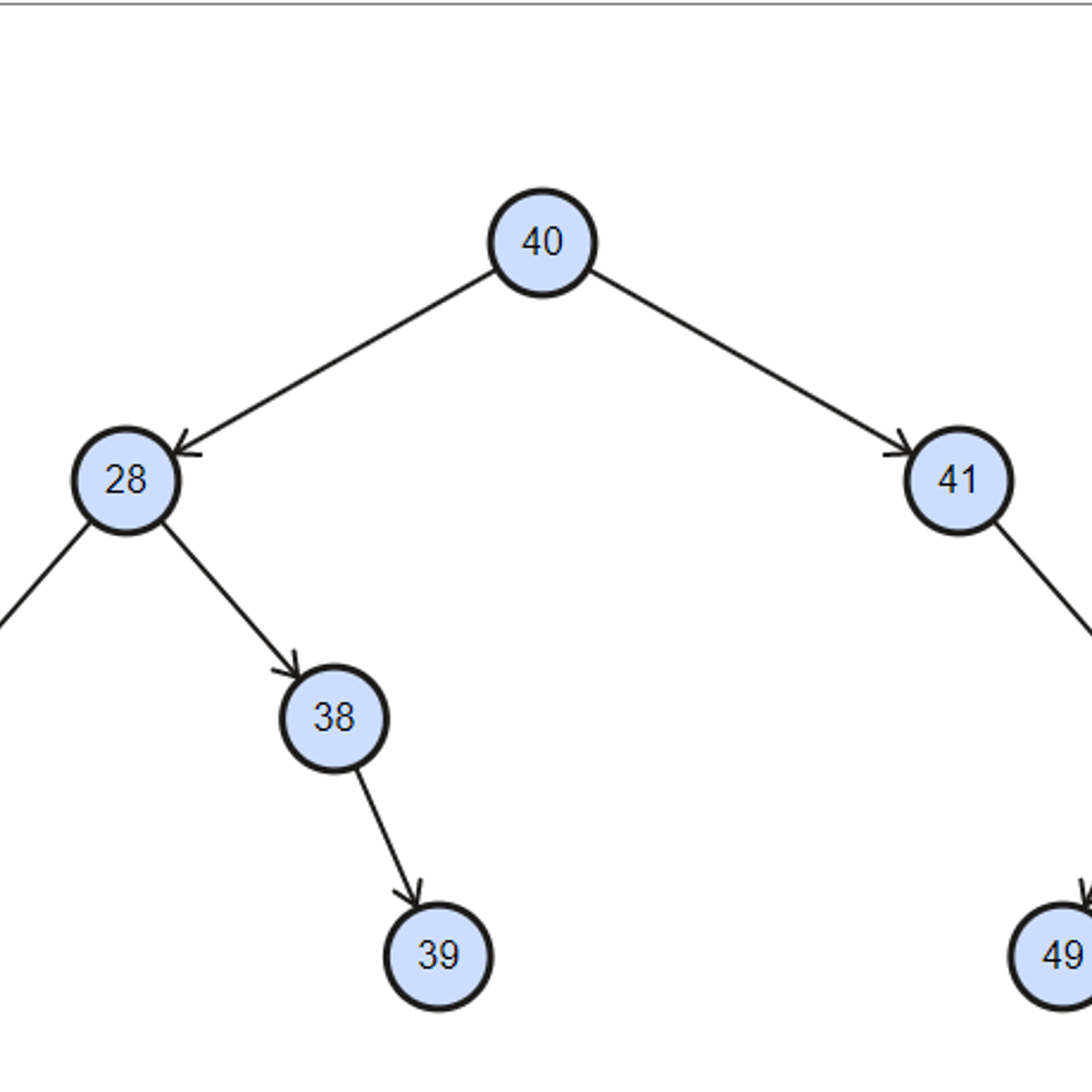
The fundamental unit of a Binary Search Tree is the node. Each node in a BST typically contains three key pieces of information: a key (the value used for ordering), a pointer to its left child, and a pointer to its right child. The key is what determines the node's position within the tree. The left child pointer references a subtree containing nodes with keys smaller than the current node's key, while the right child pointer references a subtree with keys larger than the current node's key. If a node does not have a left or right child, the respective pointer is typically set to null or a similar indicator of an empty link.
Pointers are crucial for navigating the tree. They establish the relationships between nodes, forming the hierarchical structure of the BST. When you search for a key, insert a new key, or delete an existing key, you are essentially following these pointers based on comparisons with the keys stored in the nodes. Understanding how these pointers are manipulated during various operations is key to understanding how BSTs function.
For individuals beginning their journey in computer science or considering a career change into tech, grasping the concept of nodes and pointers is a significant first step. It's a concept that extends beyond BSTs and is fundamental to many other data structures like linked lists, graphs, and more complex tree variants. Mastering this will provide a strong base for tackling more advanced topics.
These courses can help build a solid foundation in data structures, including the node and pointer concepts essential for understanding Binary Search Trees.
The following book is a classic and provides comprehensive coverage of fundamental algorithms and data structures.
Tree Height and Balance
The height of a Binary Search Tree is the length of the longest path from the root node to any leaf node. A leaf node is a node with no children. The height of a tree is a critical factor in determining its performance for operations like search, insertion, and deletion. In the best-case scenario, where the tree is perfectly balanced, the height is logarithmic with respect to the number of nodes (O(log n)). This logarithmic height is what gives BSTs their efficiency.
However, BSTs can become unbalanced. This typically happens when data is inserted in a sorted or nearly sorted order. In such a worst-case scenario, the tree can degenerate into a structure resembling a linked list, where the height becomes linear (O(n)). When a BST is unbalanced, its performance degrades significantly, and the advantages over simpler data structures like arrays or linked lists are lost. For example, searching in a degenerate BST becomes as slow as searching in a linked list.
The concept of balance is therefore crucial. A balanced BST is one where the heights of the left and right subtrees of any node differ by at most one. Various self-balancing BST algorithms, such as AVL trees and Red-Black trees, have been developed to automatically maintain balance as nodes are inserted or deleted. These structures perform rotations and other adjustments to ensure the tree remains reasonably balanced, thus preserving the O(log n) performance for key operations. Understanding the trade-offs between the complexity of maintaining balance and the performance gains achieved is a key aspect of advanced data structure design.
For those aspiring to roles in software development or data science, a clear understanding of tree height and balance is essential. It informs decisions about which data structures to use for a given problem and highlights the importance of considering worst-case scenarios in algorithm design.
These courses delve deeper into tree structures, including aspects of height and balance, which are crucial for optimizing BST performance.
To further explore the theoretical underpinnings of algorithm efficiency and data structure performance, consider these topics:
In-order, Pre-order, Post-order Traversal
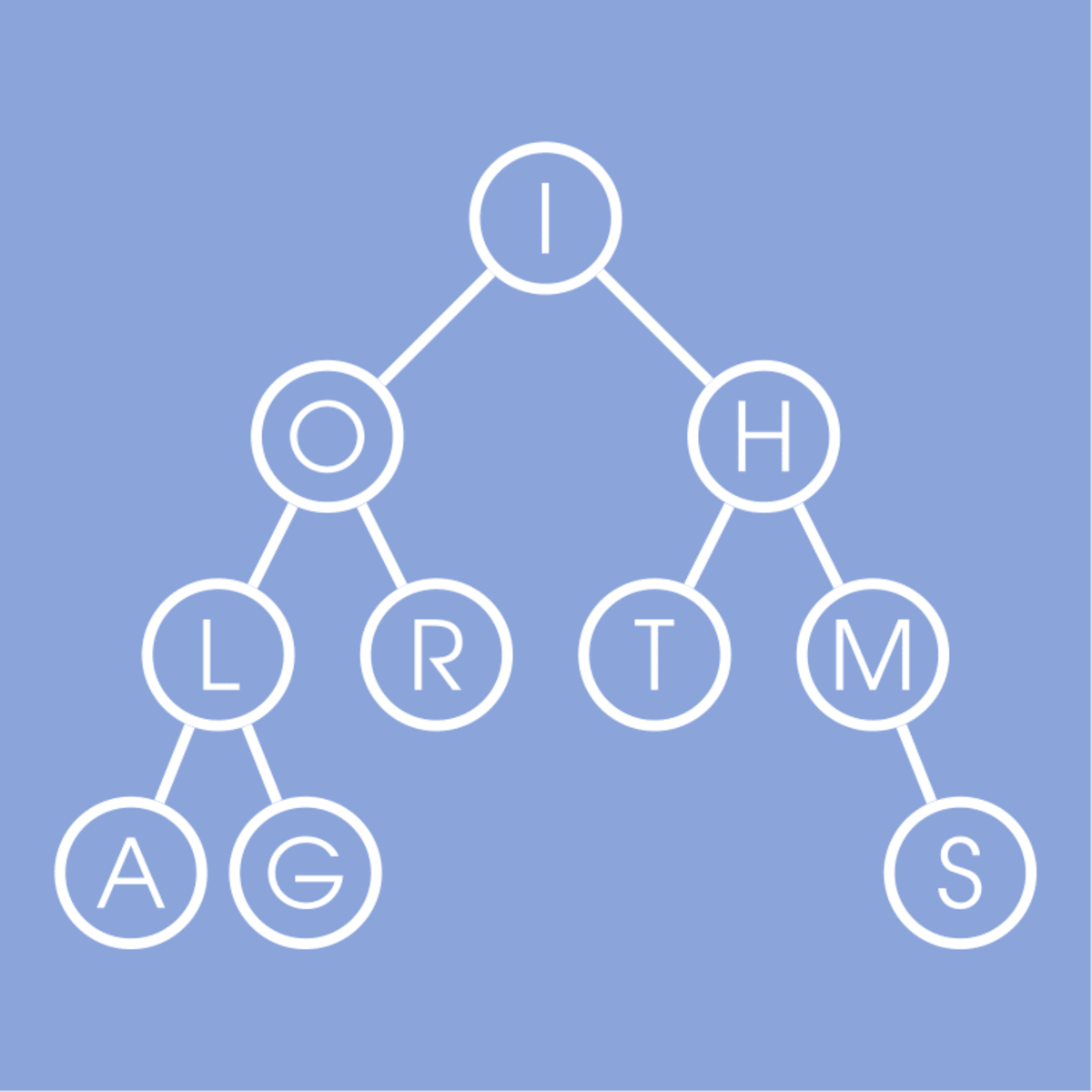
Traversing a Binary Search Tree means visiting each node in the tree exactly once in a systematic way. There are three common depth-first traversal methods: in-order, pre-order, and post-order traversal. Each method visits the nodes in a different sequence, and the choice of traversal depends on the specific task at hand.
In-order traversal visits the left subtree, then the current node, and finally the right subtree. A key property of in-order traversal on a BST is that it visits the nodes in ascending order of their keys. This makes it particularly useful for tasks like printing all the elements of the BST in sorted order.
Pre-order traversal visits the current node first, then the left subtree, and then the right subtree. This traversal is often used to create a copy of the tree or to get a prefix expression from an expression tree. For example, if you want to serialize a tree to save it to a file and then reconstruct it later, pre-order traversal is a common choice.
Post-order traversal visits the left subtree, then the right subtree, and finally the current node. This method is useful when you need to process the children of a node before the node itself, such as when deleting nodes in a tree to ensure all child nodes are freed before the parent node.
Understanding these traversal methods is fundamental for anyone working with tree-based data structures. They are not just theoretical concepts but are actively used in implementing various tree algorithms. For those preparing for technical interviews, questions involving tree traversals are very common.
The following courses offer practical insights into implementing and utilizing tree traversal techniques.
This book provides detailed explanations and examples of tree traversal algorithms.
Time Complexity Analysis (Search, Insert, Delete)
The efficiency of Binary Search Tree operations is typically measured by their time complexity, which describes how the runtime of an operation grows as the number of nodes (n) in the tree increases. For a balanced BST, the three primary operations – search, insertion, and deletion – all have an average and best-case time complexity of O(log n). This logarithmic complexity means that even as the tree grows very large, the time taken to perform these operations increases very slowly. This efficiency is a major reason why BSTs are widely used.
The search operation in a balanced BST is efficient because, at each step, we can eliminate roughly half of the remaining nodes. We start at the root and compare the target value with the current node's key. If the target is smaller, we go to the left child; if larger, we go to the right child. This process continues until the value is found or we reach a null pointer, indicating the value is not in the tree.
Insertion also typically takes O(log n) time in a balanced BST. To insert a new node, we first search for the appropriate position for the new key (as if we were searching for it). Once a null pointer is reached, the new node is inserted there as a new leaf. Similarly, deletion involves finding the node to be deleted (O(log n)) and then restructuring the tree, which also takes O(log n) on average in a balanced tree. Deletion can be more complex than insertion, as it requires handling different cases: deleting a leaf node, a node with one child, or a node with two children.
However, it's crucial to remember that these O(log n) complexities rely on the tree being reasonably balanced. In the worst-case scenario (an unbalanced tree that resembles a linked list), the time complexity for these operations degrades to O(n), as we might have to traverse all nodes. This is why balanced BST variants like AVL trees and Red-Black trees are important in practice, as they guarantee O(log n) worst-case performance by maintaining tree balance, albeit with some overhead for the balancing operations themselves.
For aspiring software engineers and computer scientists, a firm grasp of time complexity analysis is non-negotiable. It's what allows developers to make informed decisions about algorithm and data structure selection to build efficient and scalable software. Understanding these concepts is also critical for success in technical interviews.
To gain a deeper understanding of algorithmic efficiency and analysis, these resources are highly recommended:
A foundational text for algorithms, including detailed complexity analysis, is:
You may also find these topics relevant to understanding the performance characteristics of data structures:
Operations in Binary Search Trees
Understanding the core operations of a Binary Search Tree—insertion, deletion, and search—is essential for anyone looking to implement or utilize this data structure effectively. These operations are the building blocks for many applications that rely on BSTs for efficient data management.
Insertion Algorithms
Inserting a new element into a Binary Search Tree involves finding the correct position for the new node while maintaining the BST property: all keys in the left subtree must be less than the node's key, and all keys in the right subtree must be greater. The process typically begins at the root of the tree.
The algorithm compares the key of the new node with the key of the current node. If the new key is less than the current node's key, the algorithm moves to the left child. If the new key is greater, it moves to the right child. This process is repeated, traversing down the tree, until a null pointer is encountered. This null pointer indicates the position where the new node should be inserted as a leaf node. If a node with the same key already exists, the handling can vary: some BST implementations might allow duplicate keys (often placing them in the right subtree), while others might disallow duplicates or update the existing node's associated value.
The efficiency of the insertion operation is directly related to the height of the tree. In a balanced BST, insertion takes O(log n) time on average. However, if the tree is unbalanced, the insertion time can degrade to O(n) in the worst case, for instance, when inserting elements in sorted order into a naive BST. This highlights the importance of balancing mechanisms for maintaining performance in dynamic datasets.
Learning to implement insertion algorithms is a practical skill for computer science students and developers. It reinforces understanding of pointer manipulation and recursive or iterative tree traversal. Online platforms like OpenCourser's programming section offer a wealth of resources to practice these implementations in various languages.
These courses provide detailed instruction and examples for implementing BST insertion algorithms:
For a comprehensive understanding of data structure implementations, including BSTs, consider this authoritative book:
Deletion Scenarios (Leaf, Single-Child, Two-Child Nodes)
Deleting a node from a Binary Search Tree is more complex than insertion because simply removing a node can disrupt the BST property. The algorithm must handle three distinct scenarios based on the number of children the node to be deleted has: the node is a leaf, the node has one child, or the node has two children.
Deleting a leaf node: This is the simplest case. The node is removed, and the corresponding pointer in its parent node is set to null. The BST property remains intact.
Deleting a node with one child: In this scenario, the node is removed, and its single child is linked directly to the parent of the deleted node. Essentially, the child "takes the place" of the deleted node. The BST property is preserved.
Deleting a node with two children: This is the most complex case. The node to be deleted cannot be simply removed, as it would leave two disconnected subtrees. Instead, its key (and any associated data) is replaced by the key of its in-order successor (the smallest key in its right subtree) or its in-order predecessor (the largest key in its left subtree). After the replacement, the in-order successor (or predecessor), which by definition has at most one child, is then deleted using one of the simpler deletion rules described above. This ensures the BST property is maintained throughout the tree.
Like insertion, the time complexity for deletion in a balanced BST is typically O(log n), as it involves a search followed by pointer manipulations. However, in an unbalanced tree, it can degrade to O(n). Understanding these deletion scenarios and their correct implementation is crucial for maintaining the integrity and efficiency of a BST.
The following courses cover the intricacies of BST deletion, providing examples and exercises to solidify understanding.
This book offers in-depth explanations of algorithms for various data structures, including BST deletion strategies.
Search Optimization Techniques
The primary advantage of a Binary Search Tree is its ability to perform searches efficiently, ideally in O(log n) time. However, this optimal performance relies on the tree being balanced. Several techniques and considerations can optimize search operations or ensure that this efficiency is maintained.
The most fundamental "optimization" is ensuring the tree remains balanced. As discussed earlier, unbalanced trees can lead to O(n) search times. Therefore, using self-balancing BST variants like AVL trees or Red-Black trees is a critical optimization strategy for applications with frequent insertions and deletions that might otherwise lead to imbalance. These structures perform rotations and other adjustments during modifications to keep the tree height logarithmic.
Another consideration, though less about changing the BST structure itself, is understanding data access patterns. If certain keys are accessed much more frequently than others, specialized structures built upon BST principles, like splay trees, can be beneficial. Splay trees restructure themselves on every access, moving frequently accessed nodes closer to the root, thereby speeding up subsequent searches for those specific nodes. However, this comes at the cost of potentially slower operations for less frequently accessed nodes and more complex implementation.
For very large datasets that don't fit entirely in memory, B-trees and their variants (which are not binary trees but share similar hierarchical, ordered principles) are used in database and file system indexing. They are optimized for disk I/O by having a higher branching factor, reducing the height of the tree and thus the number of disk accesses required for a search. While distinct from BSTs, understanding BST search principles is a good foundation for learning about these more complex disk-based structures.
Finally, ensuring that the comparison function used to order keys is efficient is also a subtle but important aspect. If comparing keys is itself a time-consuming operation, it will impact the overall search performance regardless of how well-balanced the tree is.
Courses that explore advanced data structures often cover these optimization techniques and specialized tree types.
For deeper dives into search algorithms and data structure optimizations, this classic text is invaluable:
Exploring related topics can also provide context for search optimization:
Recursive vs. Iterative Implementations
Many Binary Search Tree operations, such as traversal, search, insertion, and deletion, can be implemented using either recursive or iterative approaches. Both have their own advantages and trade-offs, and the choice between them can depend on factors like code clarity, performance considerations, and the specific problem being solved.
Recursive implementations often mirror the natural, hierarchical definition of a tree. A function operating on a node will typically call itself for the left and/or right children. This can lead to concise and elegant code that is easier to understand, especially for operations like traversal. For example, an in-order traversal can be expressed very simply with recursion: recursively traverse the left subtree, process the current node, then recursively traverse the right subtree. However, recursion can have drawbacks. Deeply recursive calls can lead to stack overflow errors if the tree is very tall (especially if it's unbalanced). There can also be some function call overhead associated with recursion.
Iterative implementations use loops and often an explicit data structure, like a stack or queue, to manage the nodes to be visited or processed. For instance, an iterative in-order traversal might use a stack to keep track of nodes to visit. Iterative solutions can sometimes be more efficient in terms of memory (avoiding deep recursion stacks) and may offer finer control over the execution flow. However, iterative code for tree operations can sometimes be more complex and less intuitive to write and debug compared to its recursive counterpart, especially for beginners.
In practice, for many BST operations, the performance difference between a well-written recursive solution and a well-written iterative solution might be negligible for moderately sized, balanced trees. However, for extremely large or unbalanced trees, the potential for stack overflow with recursion becomes a more significant concern. Many standard library implementations of tree-based structures might use iterative approaches internally for robustness and performance, or employ techniques to limit recursion depth.
Understanding both approaches is valuable for a well-rounded computer science education. It allows developers to choose the most appropriate implementation strategy based on the specific requirements and constraints of their application. For those preparing for technical interviews, being able to discuss and implement both recursive and iterative solutions for tree problems is often expected.
These courses provide opportunities to see and implement both recursive and iterative solutions for data structure operations.
This book discusses various implementation strategies for algorithms, touching upon recursive and iterative methods.
Exploring the broader concept of algorithms will also shed light on these different implementation paradigms.
Applications of Binary Search Trees
Binary Search Trees are not just a theoretical concept; they have numerous practical applications across various domains in computer science. Their ability to efficiently manage sorted data makes them a valuable tool for developers and engineers. Understanding these applications can provide motivation and context for learning about BSTs.
Database Indexing Mechanisms
One of the most significant applications of Binary Search Trees (and their more complex relatives like B-trees and B+ trees) is in database indexing. An index in a database is a data structure that improves the speed of data retrieval operations on a database table. Instead of scanning an entire table to find a specific row or set of rows (which can be very slow for large tables), the database can use an index to quickly locate the desired data.
BSTs, or variants optimized for disk-based storage, can be used to store the indexed column values in a sorted order. When a query with a condition on an indexed column is executed (e.g., WHERE userID = 123 or WHERE lastName > 'Smith'), the database's query optimizer can use the BST-like index to perform a fast search (similar to a BST search operation) to find the pointers to the actual data rows that satisfy the condition. This dramatically reduces the number of disk I/O operations needed, which is often the bottleneck in database performance.
While simple BSTs might be used for in-memory indexes or smaller datasets, large-scale relational databases typically use B-trees or B+ trees. These structures are specifically designed for efficient disk access by having a higher branching factor (more children per node), which reduces the tree's height and thus the number of disk reads required to traverse from the root to a leaf. However, the fundamental principle of using an ordered tree structure to speed up searches is derived from the concepts underlying BSTs.
For individuals interested in database administration, backend development, or data engineering, understanding indexing mechanisms is crucial. Knowledge of how BSTs contribute to these mechanisms provides a solid foundation for designing efficient database schemas and writing performant queries. More information on database concepts can be found on OpenCourser's Data Science section.
While these courses may not focus exclusively on database indexing, they provide the foundational knowledge of data structures like BSTs that are used in indexing.
This book delves into algorithms used in various systems, including those relevant to database operations.
Exploring the topic of databases more broadly will reveal the importance of efficient indexing.
File System Hierarchies
Binary Search Trees, and more generally tree structures, are conceptually related to how file systems organize files and directories. Most modern operating systems use a hierarchical file system, where directories can contain files and other subdirectories, forming a tree-like structure. The root directory is the top-most node, and paths to files represent traversals down this tree.
While the actual on-disk implementation of a file system directory might use various data structures (like B-trees, hash tables, or linear lists of directory entries, depending on the file system like NTFS, ext4, HFS+), the logical organization is inherently a tree. When you navigate through folders or when the operating system searches for a file, it's conceptually traversing this file system tree.
Although a standard file system directory isn't typically a direct BST implementation (as directories often store files by name, and the order might not strictly follow BST rules for all operations), the tree structure allows for efficient organization and retrieval. Operations like listing directory contents, finding a file by path, or recursively processing all files in a directory and its subdirectories are all tree traversal operations. For certain specialized file system operations or metadata management, BST-like structures could be employed internally to optimize searching for specific attributes or managing directory entries efficiently, especially if they need to be kept sorted for some reason.
Understanding tree structures, including BSTs, provides a good mental model for how file systems are organized. This knowledge can be beneficial for software developers who need to interact with the file system programmatically, for system administrators managing storage, or for anyone curious about the inner workings of their operating system. Exploring IT & Networking topics on OpenCourser can provide further context.
Courses on operating systems or advanced data structures often touch upon file system design and the data structures involved.
This book covers a wide range of computer science topics, including foundational data structures that underpin systems like file organization.
Game Development (Spatial Partitioning)
In game development, particularly in 3D games, efficiently determining which objects are visible to the camera or which objects might collide with each other is crucial for performance. Spatial partitioning techniques are used to divide the game world into smaller, manageable regions. Tree structures, including variants and relatives of Binary Search Trees like k-d trees and BSP (Binary Space Partitioning) trees, play a significant role here.
A Binary Space Partitioning (BSP) tree, for example, is a method of recursively dividing a space into two subspaces by a hyperplane. This creates a tree structure where each node represents a region of space, and its children represent the two sub-regions created by a partitioning plane. BSP trees are commonly used for visibility determination (e.g., quickly culling objects that are not in the player's view frustum) and collision detection (by limiting collision checks to objects within the same or nearby spatial regions).
While not identical to a standard key-ordered BST, the hierarchical subdivision and search principles are similar. The tree structure allows the game engine to quickly discard large portions of the game world that are irrelevant to the current camera view or a specific collision query. This avoids having to check every object against every other object, which would be computationally prohibitive in complex game environments.
For aspiring game developers or those interested in computer graphics and computational geometry, understanding spatial partitioning techniques and the underlying tree data structures is essential. These concepts are fundamental to building performant and interactive game worlds. Many Computer Science courses on OpenCourser cover the algorithmic foundations relevant to these applications.
While specific courses on game development using BSTs might be niche, understanding core data structures is a prerequisite. These courses build that foundation:
Understanding algorithms is key to game development optimization.
Real-World Libraries/Frameworks Using BSTs
Binary Search Trees, particularly their self-balancing variants like Red-Black trees and AVL trees, are implemented in many standard libraries and frameworks across various programming languages. These implementations provide developers with efficient ways to store and retrieve ordered data without having to implement the complex tree logic from scratch.
For instance, in C++, the `std::map` and `std::set` containers are typically implemented using Red-Black trees. These containers provide O(log n) average time complexity for insertion, deletion, and search operations, and they maintain elements in sorted order. Similarly, Java's `TreeMap` and `TreeSet` collections are also based on Red-Black trees, offering similar performance characteristics and ordered iteration.
In Python, while the built-in `dict` (for dictionaries/hash maps) and `set` are implemented using hash tables (providing O(1) average time complexity for lookups but not maintaining order), libraries are available that provide sorted collection types often based on balanced BST principles if ordered iteration or range queries are needed. Many other programming languages and their standard libraries offer analogous data structures that rely on balanced BSTs for efficient ordered associative arrays or sets.
Beyond standard language libraries, BST principles are also found in various specialized software. For example, some network routers might use tree-like structures (like binary tries or Patricia tries, which are related to trees) for efficient IP address lookups and packet forwarding. Compilers often use Abstract Syntax Trees (ASTs), which are tree representations of source code, and while not BSTs themselves, the manipulation and traversal of these trees share common algorithmic techniques.
Recognizing where BSTs and similar tree structures are used in common tools and libraries can help developers make informed choices about data structures for their own applications. It also underscores the practical importance of understanding these foundational concepts. If you're learning a new programming language, exploring its standard library for ordered collection types can often lead you to implementations based on balanced BSTs.
Courses that teach programming languages in depth often cover their standard libraries, including tree-based collections.
Books on specific programming languages often detail the implementation and usage of their core data structures.
Understanding the core data structures of popular programming languages is beneficial.
Balanced vs. Unbalanced Binary Search Trees
A crucial aspect of working with Binary Search Trees is understanding the difference between balanced and unbalanced trees. This distinction directly impacts the performance and reliability of BST-based applications, especially when dealing with dynamic data that changes frequently.
Performance Degradation in Worst-Case Scenarios
The primary appeal of a Binary Search Tree is its potential for O(log n) performance for search, insertion, and deletion operations. However, this efficiency is contingent upon the tree maintaining a relatively balanced structure. In an unbalanced BST, the height of the tree can become disproportionately large compared to the number of nodes it contains.
The worst-case scenario occurs when the tree becomes completely skewed, essentially degenerating into a linked list. This can happen if elements are inserted in a strictly sorted (ascending or descending) order into a naive BST implementation that doesn't perform any balancing. In such a degenerate tree with 'n' nodes, the height of the tree becomes 'n' (or n-1), rather than log n. Consequently, operations that depend on the tree's height, like searching for an element, inserting a new element, or deleting an element, will take O(n) time in the worst case. This is no better than the performance of a simple linked list or an unsorted array for these operations, thereby negating the primary advantage of using a BST.
This performance degradation can be a significant issue in real-world applications where input data patterns are unpredictable or can sometimes be ordered. If a system relies on the O(log n) efficiency of a BST but encounters worst-case input, it can lead to unexpected slowdowns and a poor user experience. Therefore, understanding and mitigating the risk of unbalanced trees is a critical consideration for software developers.
For those learning about data structures, recognizing this potential pitfall is as important as understanding the ideal-case behavior. It motivates the need for more sophisticated tree structures that can maintain balance.
Courses focusing on data structures and algorithms will typically cover the performance characteristics of BSTs, including worst-case scenarios.
This book offers a thorough treatment of algorithms and their performance analysis.
Introduction to AVL Trees and Red-Black Trees
To counteract the performance degradation of unbalanced Binary Search Trees, several types of self-balancing Binary Search Trees have been developed. Among the most well-known are AVL trees and Red-Black trees. These data structures automatically adjust their shape through specific operations (like rotations) during insertions and deletions to ensure that the tree remains reasonably balanced, thereby guaranteeing O(log n) worst-case time complexity for key operations.
AVL trees, named after their inventors Adelson-Velsky and Landis, are strictly balanced. For every node in an AVL tree, the heights of its left and right subtrees can differ by at most one. This strict balance criterion ensures that the tree's height is always close to the optimal log n. When an insertion or deletion violates this balance factor, the tree performs one or more "rotations" to restore the property. While AVL trees offer excellent search performance due to their strict balance, the balancing operations themselves can sometimes be more frequent or complex compared to other self-balancing trees.
Red-Black trees are another type of self-balancing BST that uses a set of rules and node coloring (red or black) to maintain balance. The rules for Red-Black trees are designed to ensure that no path from the root to a leaf is more than twice as long as any other path, which keeps the tree approximately balanced and guarantees O(log n) height. Red-Black trees are often preferred in practice for implementations of maps and sets in standard libraries (like C++ STL's `std::map` or Java's `TreeMap`) because they generally have slightly lower constant factors for insertion and deletion operations compared to AVL trees, even if their balance might not be as strict.
Understanding the existence and purpose of these self-balancing trees is important for anyone working seriously with data structures. While their implementation details can be complex, knowing when to use them (i.e., when worst-case performance guarantees are critical) is a key aspect of good software design. Many advanced algorithm courses delve into the specifics of these structures.
These courses often cover advanced tree structures, including introductions to AVL and Red-Black trees.
For a deeper understanding of these self-balancing structures, this book is an excellent resource:
Exploring balanced tree concepts is a natural next step after understanding basic BSTs.
Rotation Operations for Balancing
Rotation operations are the fundamental mechanism by which self-balancing Binary Search Trees, like AVL trees and Red-Black trees, maintain their balance and ensure logarithmic height. A rotation is a local transformation of a subtree that changes the parent-child relationships between nodes while preserving the BST ordering property. The goal of a rotation is to reduce the height of a taller subtree and increase the height of a shorter one, thereby making the overall tree more balanced.
There are two basic types of rotations: left rotation and right rotation.
A left rotation around a node 'x' (which has a right child 'y') makes 'y' the new root of the subtree, with 'x' becoming 'y's left child. The original left child of 'y' becomes the new right child of 'x'. This operation is performed when the right subtree of 'x' becomes too heavy.
Conversely, a right rotation around a node 'y' (which has a left child 'x') makes 'x' the new root of the subtree, with 'y' becoming 'x's right child. The original right child of 'x' becomes the new left child of 'y'. This is used when the left subtree of 'y' is too heavy.
In self-balancing trees like AVL trees, rotations are performed when an insertion or deletion operation causes the "balance factor" of a node (the difference in height between its left and right subtrees) to exceed a certain threshold (typically 1). Depending on the specific imbalance, a single rotation (left or right) or a double rotation (e.g., a left rotation followed by a right rotation, or vice-versa) might be necessary to restore the balance property. Red-Black trees also use rotations, in conjunction with color changes, to maintain their balance invariants after insertions or deletions.
While the exact conditions and sequences of rotations differ between various types of self-balancing trees, the core idea of restructuring the tree locally to maintain overall balance is common. Understanding the mechanics of rotations is key to comprehending how these advanced data structures achieve their guaranteed performance. For students and developers, visualizing these rotations can be very helpful in grasping the concepts.
Advanced data structure courses often include detailed explanations and visualizations of tree rotations.
This comprehensive text explains rotation operations in the context of balanced trees.
Trade-offs Between Complexity and Efficiency
When choosing between a standard (unbalanced) Binary Search Tree and a self-balancing BST (like an AVL tree or Red-Black tree), it's essential to consider the trade-offs between implementation complexity and operational efficiency. There's no single "best" choice for all scenarios; the optimal data structure depends on the specific requirements of the application.
A standard, naive BST is relatively simple to implement. The logic for search, insertion, and deletion (especially for leaf nodes or nodes with one child) is straightforward. However, as discussed, its performance can degrade to O(n) in the worst case if the tree becomes unbalanced. This makes it unsuitable for applications where consistent performance is critical or where input data might lead to skewed trees.
Self-balancing BSTs, on the other hand, guarantee O(log n) worst-case time complexity for key operations. This predictable and efficient performance is highly desirable for many applications. However, this efficiency comes at the cost of increased implementation complexity. The algorithms for insertion and deletion in AVL or Red-Black trees must include logic for performing rotations and (in the case of Red-Black trees) color changes to maintain balance. This makes the code more intricate, harder to debug, and potentially introduces a small constant factor overhead to each modification operation due to the balancing work.
So, the decision involves weighing these factors:
- If the dataset is relatively static or if insertions and deletions are rare and unlikely to create severe imbalances, a simple BST might suffice, offering ease of implementation.
- If the application involves frequent insertions and deletions, and predictable O(log n) performance is crucial even in worst-case scenarios, then a self-balancing BST is generally the better choice, despite its higher implementation complexity. Most general-purpose libraries opt for self-balancing trees for their ordered map/set implementations for this reason.
For learners and developers, understanding these trade-offs is a hallmark of a maturing understanding of data structures and algorithms. It's about choosing the right tool for the job, considering not just the best-case performance but also worst-case behavior and development effort. OpenCourser's Learner's Guide provides resources on how to structure self-learning to tackle such nuanced topics effectively.
Courses that compare different data structures often highlight these kinds of trade-offs.
This book is renowned for its in-depth analysis of algorithms, including the complexities of various data structures.
Understanding algorithmic complexity is fundamental here.
Career Pathways Involving Binary Search Trees
A solid understanding of Binary Search Trees and other fundamental data structures is a cornerstone of a career in software development and related fields. While "Binary Search Tree Expert" isn't typically a job title, the knowledge is implicitly required for many technical roles and can significantly influence career progression.
Roles Requiring BST Expertise (e.g., Backend Engineers, Database Architects)
Several roles in the tech industry directly or indirectly benefit from a strong understanding of Binary Search Trees and related data structures.
Software Engineers (Backend, Systems, Generalists): Developers working on the server-side of applications, building system-level software, or even creating complex frontend components often encounter scenarios where efficient data management, searching, and sorting are critical. Knowledge of BSTs helps in choosing or designing appropriate data structures for performance-critical parts of an application. Many standard libraries for storing ordered collections (like maps or sets) are implemented using balanced BSTs, so understanding their behavior is key to using these libraries effectively. According to the U.S. Bureau of Labor Statistics, employment for software developers is projected to grow significantly, indicating a continued demand for these skills.
Database Architects and Developers: As discussed, BST principles are fundamental to database indexing. Professionals designing database schemas, optimizing queries, or developing database management systems themselves must have a deep understanding of how indexes work, including the tree-based structures that often power them.
Algorithm Developers: For those specializing in designing and implementing novel algorithms, a thorough grasp of various data structures, including all forms of trees, is essential. This role often involves research and development in areas like machine learning, artificial intelligence, or high-performance computing.
Game Developers: As mentioned, spatial partitioning techniques in game development often rely on tree structures like BSP trees or k-d trees. Performance is paramount in gaming, and efficient data structures are key.
Even for roles not directly focused on low-level implementation, such as Data Scientists or Machine Learning Engineers, understanding data structures can be beneficial. For example, decision tree algorithms, a common machine learning technique, are inherently tree-based. While these are not BSTs, the general concepts of tree traversal, construction, and complexity are transferable. Exploring career paths on OpenCourser can help individuals identify roles that align with their technical interests.
These courses can help build the foundational skills in data structures and algorithms often required for these roles.
Consider exploring these related career paths:
Interview Preparation Strategies
Questions related to Binary Search Trees and other tree structures are a staple of technical interviews for software engineering roles, especially at competitive tech companies. Interviewers use these questions to assess a candidate's understanding of fundamental data structures, algorithmic thinking, problem-solving skills, and coding proficiency.
Effective preparation strategies include:
Mastering the Fundamentals: Ensure a solid understanding of BST properties, node structure, insertion, deletion (all cases), search, and traversal methods (in-order, pre-order, post-order). Be comfortable with both recursive and iterative implementations.
Understanding Time and Space Complexity: For any solution you propose, be prepared to analyze its time and space complexity, including best, average, and worst-case scenarios. Explain why a BST might be chosen over other structures like hash tables or arrays for a given problem.
Practicing Common Problems: Work through a variety of common BST interview questions. These often include:
- Validating if a given binary tree is a BST.
- Finding the k-th smallest/largest element.
- Finding the lowest common ancestor (LCA) of two nodes.
- Converting a sorted array/linked list to a balanced BST.
- Tree traversals (and variations like level-order traversal).
- Problems involving tree height, diameter, or checking for balance.
Coding on a Whiteboard or Shared Document: Practice writing code by hand or in a plain text editor, as this is common in interviews. Focus on clarity, correctness, and handling edge cases (e.g., an empty tree, a tree with one node).
Articulating Your Thought Process: Interviewers are interested in how you approach a problem. Think out loud, explain your reasoning, discuss trade-offs of different approaches, and be open to hints or clarifications.
Learning About Balanced Trees: While you might not be asked to implement an AVL or Red-Black tree from scratch in most generalist interviews (due to their complexity), understanding their purpose and when they are used is important.
Many online platforms like LeetCode, HackerRank, and GeeksforGeeks offer a vast collection of tree-based coding problems for practice.
These courses are specifically designed to help with coding interview preparation, often covering tree problems extensively.
This book is a well-regarded resource for technical interview preparation.
Open-Source Contribution Opportunities
Contributing to open-source projects can be an excellent way for aspiring and established developers to hone their skills, gain practical experience, build a portfolio, and collaborate with others in the software development community. While finding open-source projects that *exclusively* focus on implementing basic Binary Search Trees might be rare (as these are often part of standard libraries), there are numerous opportunities to work with tree structures and apply BST knowledge in broader contexts.
Consider looking for projects involving:
- Libraries and Frameworks: Many open-source libraries that provide data structures, collections, or utility functions might have opportunities to improve existing tree-based implementations, add new features, enhance documentation, or write more comprehensive tests. This could involve working with balanced BSTs or other tree variants.
- Database Systems: Open-source databases (SQL or NoSQL) often have complex indexing mechanisms and query optimizers. Contributions could involve working on parts of these systems that use tree-like structures for indexing or query plan representation.
- Compilers and Interpreters: These tools heavily rely on Abstract Syntax Trees (ASTs) to represent code. While not BSTs, working with ASTs involves tree traversal, manipulation, and optimization – skills that are related to general tree expertise.
- Scientific Computing and Data Analysis Tools: Some tools in these domains might use specialized tree structures for tasks like spatial indexing, hierarchical clustering, or efficient searching in large datasets.
To find such opportunities, you can explore platforms like GitHub by searching for issues tagged with "data structures," "algorithms," "good first issue," or specific technologies you're interested in. Look for projects that align with your skill level and interests. Starting with smaller contributions, like fixing bugs, improving documentation, or adding test cases, can be a good way to get familiar with a project's codebase and contribution process.
Engaging with the open-source community not only enhances technical skills but also demonstrates initiative and a passion for software development, which can be attractive to potential employers. Many developers find that their open-source contributions lead to valuable learning experiences and even career opportunities.
While not direct courses on open-source contribution, building strong foundational skills through courses like these is essential before diving into complex projects.
Skill Transferability to Graph-Based Problems
The knowledge and skills gained from learning about Binary Search Trees are highly transferable, particularly to understanding and solving graph-based problems. Trees are, in fact, a special type of graph – specifically, they are connected acyclic graphs. Many concepts and algorithms used with trees have analogous or more generalized versions in graph theory.
Traversal Algorithms: Depth-First Search (DFS) and Breadth-First Search (BFS) are fundamental traversal algorithms for graphs. The in-order, pre-order, and post-order traversals learned for BSTs are specific forms of DFS. Understanding how DFS explores a tree by going as deep as possible along each branch before backtracking is directly applicable to how DFS explores paths in a general graph. Similarly, while BSTs don't typically use BFS for standard operations, understanding BFS (often introduced alongside tree level-order traversal) is crucial for many graph algorithms like finding the shortest path in an unweighted graph.
Node and Edge Concepts: The idea of nodes (vertices) connected by pointers (edges) is central to both trees and graphs. Manipulating these structures, keeping track of visited nodes, and understanding adjacency are skills developed with trees that apply directly to graphs.
Recursive Thinking: Many tree algorithms are elegantly expressed recursively due to the inherent recursive structure of trees. This recursive problem-solving mindset is also invaluable for tackling graph problems, many of which can be broken down into smaller subproblems on subgraphs or neighboring nodes.
Pathfinding and Connectivity: Problems like finding a path between two nodes, checking for connectivity, or finding cycles, which are common in graph theory, have simpler counterparts in trees (e.g., finding the path between two nodes in a tree, or the fact that trees are inherently acyclic). The foundational understanding gained from trees helps in approaching these more complex graph scenarios.
Many real-world problems are modeled using graphs, including social networks, transportation systems, web page linkages, and dependencies in software projects. Therefore, the ability to work with graph algorithms is a highly valuable skill for software engineers and data scientists. A strong foundation in tree data structures, like BSTs, provides an excellent stepping stone into the richer and more complex world of graph theory and its applications. Exploring topics in Data Science on OpenCourser can often lead to applications of graph algorithms.
Courses that cover both trees and graphs often highlight these connections and transferable skills.
This comprehensive text covers both tree and graph algorithms in detail.
Delving into these related topics can broaden your understanding:
Formal Education Pathways
For those seeking a structured approach to mastering Binary Search Trees and the broader field of computer science, formal education pathways offer comprehensive curricula, expert guidance, and recognized credentials. These routes are particularly well-suited for individuals at the pre-university stage, current university students, and those considering graduate studies.
Relevant Undergraduate Courses (Data Structures, Algorithms)
The cornerstone of understanding Binary Search Trees within a formal undergraduate computer science or software engineering curriculum typically lies within two key courses: Data Structures and Algorithms. These courses are usually taken after introductory programming courses.
A typical Data Structures course will introduce fundamental ways of organizing and storing data. Binary Search Trees are a major topic, usually covered after linear structures like arrays and linked lists, and alongside other tree types like heaps or general trees. Students learn about BST properties, operations (insertion, deletion, search), different traversal methods (in-order, pre-order, post-order), and the concepts of tree height and balance. Implementations are often done in languages like Java, C++, or Python.
The Algorithms course builds upon the data structures learned, focusing on designing, analyzing, and implementing efficient algorithms. For BSTs, this involves analyzing the time and space complexity of operations (O(log n) for balanced trees, O(n) for worst-case unbalanced trees). The course will also likely cover self-balancing BSTs like AVL trees or Red-Black trees, explaining the rotation mechanisms and proving their performance guarantees. Sorting algorithms (some of which, like tree sort, use BSTs) and search algorithms (where BSTs excel) are also key components.
Beyond these core courses, concepts related to BSTs might also appear in:
- Database Systems: Discussing indexing mechanisms which often use B-trees (a relative of BSTs).
- Compiler Design: Introducing Abstract Syntax Trees.
- Operating Systems: Covering file system structures which are hierarchical.
Successfully completing these undergraduate courses provides a strong theoretical and practical foundation in BSTs and their applications, which is essential for careers in software development and further academic pursuits. Many universities offer these courses, and resources like OpenCourser's Computer Science section list numerous online options that can supplement traditional learning.
These online courses mirror the content typically found in undergraduate data structures and algorithms modules.
Foundational computer science textbooks are indispensable for undergraduate studies.
Exploring the broader field provides context.
Research Opportunities in Advanced Tree Structures
For students pursuing graduate studies (Master's or Ph.D.) in computer science, Binary Search Trees serve as a foundational concept that opens doors to research in more advanced tree structures and related algorithmic problems. While basic BSTs are well-understood, the field continues to evolve, especially concerning specialized applications, performance in modern hardware architectures, and handling massive datasets.
Research opportunities can exist in areas such as:
- New Self-Balancing Mechanisms: While AVL and Red-Black trees are classic, research may explore new balancing algorithms with different trade-offs, perhaps optimized for specific types of data or operations, or for concurrent access in multi-threaded environments.
- Cache-Oblivious and Cache-Efficient Trees: With the growing gap between CPU speed and memory access times, designing tree structures that perform well with modern memory hierarchies (caches) is an active area. This involves minimizing cache misses by arranging data in a cache-friendly manner. B-trees are an early example, but research continues for more general or adaptive structures.
- Trees for High-Dimensional Data: Standard BSTs are for one-dimensional keys. For searching in multi-dimensional spaces (e.g., geographic data, feature vectors in machine learning), structures like k-d trees, R-trees, or quadtrees are used. Research here focuses on improving their performance, handling high dimensionality ("curse of dimensionality"), and supporting various types of queries.
- Probabilistic and Randomized Tree Structures: Skip lists (which have tree-like properties) and treaps (randomized BSTs) offer good expected performance with simpler balancing logic than deterministic structures. Research might explore new randomized approaches or analyze their behavior more deeply.
- Persistent Data Structures: A persistent version of a data structure allows access to any previous version of itself after modifications. Research in persistent BSTs is relevant for functional programming, version control systems, and computational geometry.
- Tree Structures for Quantum Computing: As quantum computing evolves, researchers are exploring how data structures, including trees, can be adapted or re-envisioned for quantum algorithms, potentially offering new types of speedups or capabilities.
Graduate students often work closely with faculty advisors on such research topics, contributing to publications and advancing the field. This path requires a strong theoretical background and a passion for problem-solving.
While advanced research topics are typically pursued in university settings, foundational knowledge from these courses is essential.
Advanced texts often hint at or directly discuss areas of ongoing research.
Competitive Programming Resources
Competitive programming is a popular mind sport where participants solve complex algorithmic problems within tight time limits. Binary Search Trees and a wide array of other data structures and algorithms are fundamental tools in a competitive programmer's arsenal. Platforms like TopCoder, Codeforces, LeetCode, HackerRank, and events like the ACM International Collegiate Programming Contest (ICPC) are central to this community.
In competitive programming, BST-related problems can range from straightforward implementations to highly intricate challenges requiring deep insights. Common tasks include:
- Efficiently querying sorted data, often involving modifications (insertions/deletions).
- Problems that can be modeled using ordered sets or maps (often implemented with balanced BSTs like C++ `std::set` or `std::map`).
- Range queries (e.g., counting elements within a specific range, finding sum/min/max in a range), which might involve segment trees or Fenwick trees (BITs), which are specialized tree structures.
- Problems requiring custom modifications to BST nodes or operations.
While using built-in library versions of balanced BSTs is common for speed, sometimes problems require implementing parts of a BST or a specialized tree from scratch, or a deep understanding of their internal workings to solve a more complex variant. Knowledge of different traversal methods, understanding time complexity, and recognizing when a tree-based approach is suitable are crucial skills. Competitive programmers often spend significant time practicing problems, learning new techniques, and analyzing solutions from others.
For students interested in strengthening their problem-solving abilities and data structure knowledge, competitive programming offers an excellent, albeit challenging, avenue. Success in these competitions can also be a strong signal to potential employers, especially for roles requiring advanced algorithmic skills. Many online courses and communities are dedicated to preparing for competitive programming. OpenCourser's algorithm section is a good starting point to find relevant learning materials.
These courses are often tailored to help with the types of algorithmic problems found in competitive programming.
Classic algorithm textbooks are vital resources for competitive programmers.
Thesis/Dissertation Topics in BST Variations
For students pursuing advanced degrees (Master's or Ph.D.) in computer science, research culminating in a thesis or dissertation often involves exploring novel aspects or applications of existing concepts. Binary Search Trees, despite being a foundational topic, still offer avenues for specialized research, particularly when considering their variations, performance under specific constraints, or integration with emerging technologies.
Potential areas for thesis or dissertation topics related to BST variations could include:
- Analysis and Optimization of Concurrent BSTs: Designing and analyzing BST structures that can be safely and efficiently accessed and modified by multiple threads simultaneously is a complex challenge, crucial for multi-core processor environments.
- Memory Layout Optimization for Modern Hardware: Investigating how the memory layout of BST nodes can be optimized to improve cache performance and reduce memory latency on contemporary hardware architectures, potentially leading to new "cache-aware" or "cache-oblivious" BST designs.
- BSTs with Non-Standard Key Types or Comparison Functions: Exploring BSTs designed to handle complex key types (e.g., strings with specialized lexicographical ordering, geometric objects) or dynamic/fuzzy comparison functions.
- Energy-Efficient BST Algorithms: With the increasing focus on green computing, research into BST operations and balancing strategies that minimize energy consumption could be a relevant topic.
- Self-Adjusting BSTs Beyond Splay Trees: Investigating new heuristics or mechanisms for self-adjusting BSTs that might offer better amortized performance or adapt more effectively to specific access patterns.
- Applications of BSTs in Domain-Specific Problems: Applying or adapting BST variations to solve particular problems in fields like bioinformatics (e.g., phylogenetic trees, sequence alignment), network routing, or real-time systems, often with unique constraints or performance requirements.
- Theoretical Bounds and Properties of BST Variants: Delving into the mathematical analysis of specific BST algorithms, proving tighter bounds on their performance, or exploring their combinatorial properties.
Such research typically involves a deep dive into existing literature, formulating new hypotheses or algorithms, rigorous implementation and experimentation, and theoretical analysis. It contributes to the broader academic understanding of data structures and their capabilities.
While these are introductory, they lay the groundwork for understanding the complexities that might be explored in advanced research.
Advanced research often builds upon the foundational principles discussed in comprehensive texts.
Topics like optimal and balanced trees are rich areas for deeper study.
Self-Directed Learning Strategies
For individuals looking to learn about Binary Search Trees outside of a traditional academic setting, such as career pivoters or lifelong learners, self-directed learning offers a flexible and accessible path. With a wealth of online resources available, mastering BSTs and related concepts is achievable with dedication and a structured approach.
OpenCourser makes it easy to search for courses on Binary Search Trees and related topics from various providers, helping you find the resources that best fit your learning style and goals.
Project-Based Learning Ideas (BST Visualizers, Benchmark Tools)
One of the most effective ways to solidify understanding in a technical subject like Binary Search Trees is through project-based learning. Building tangible projects not only reinforces theoretical knowledge but also develops practical coding skills and problem-solving abilities. For BSTs, several interesting project ideas can help deepen your understanding:
BST Visualizer: Develop an application (web-based or desktop) that allows users to insert, delete, and search for nodes in a BST and visually displays the tree structure as it changes. This helps in understanding how operations affect the tree's shape and balance. You could extend it to show different traversal orders or even animate the balancing operations of an AVL or Red-Black tree if you're feeling ambitious.
Benchmark Tool for Tree Operations: Create a program that benchmarks the performance (e.g., time taken) of search, insertion, and deletion operations on different types of BSTs (e.g., naive BST vs. a self-balancing one like AVL or Red-Black, or even comparing against hash tables or sorted arrays). This project would involve implementing these data structures and running experiments with various data sizes and input patterns (e.g., random data vs. sorted data) to observe performance differences and worst-case behaviors.
Text Indexer/Search Engine: Build a simple application that takes a text document, builds an index of words using a BST (where each node stores a word and perhaps a list of its occurrences), and then allows users to search for words in the document efficiently.
Contact Book Application: Implement a contact book where contacts are stored and managed using a BST, ordered by name or another key. This would involve implementing insertion, deletion, search, and display (e.g., in-order traversal for sorted listing) functionalities.
These projects provide hands-on experience with implementing BST operations, handling edge cases, and potentially working with user interfaces or data analysis. They also serve as excellent portfolio pieces to showcase your skills to potential employers. When working on such projects, consider using version control (like Git) and documenting your code and design choices.
Many general data structures and algorithms courses provide the building blocks for such projects.
Books focusing on practical implementations can be very helpful for project-based learning.
Coding Challenge Platforms for Practice
For self-directed learners aiming to master Binary Search Trees, coding challenge platforms are invaluable resources. Websites like LeetCode, HackerRank, Codewars, Edabit, and GeeksforGeeks offer extensive collections of programming problems, many of which specifically target data structures like BSTs. These platforms provide an interactive environment to write code, test it against various inputs, and receive immediate feedback.
Practicing on these platforms helps in several ways:
- Reinforcing Concepts: Solving problems requires applying the theoretical knowledge of BST operations (search, insert, delete, traversals) in concrete scenarios.
- Developing Problem-Solving Skills: Many challenges are not straightforward implementations but require adapting BST concepts or combining them with other algorithmic techniques to arrive at a solution.
- Improving Coding Proficiency: Regularly writing code helps in becoming more fluent in a chosen programming language and in writing cleaner, more efficient code.
- Interview Preparation: A significant portion of problems on these platforms are representative of what's asked in technical interviews at software companies.
- Learning Different Approaches: Most platforms allow viewing solutions submitted by others after solving a problem (or attempting it). This can expose you to different ways of thinking and more optimal solutions.
When using these platforms, it's beneficial to start with easier problems to build confidence and then gradually move to more complex ones. Focus not just on getting the correct answer, but also on understanding the time and space complexity of your solution and whether it can be optimized. Many platforms also have discussion forums where users can ask questions and share insights about problems. For those on a budget, OpenCourser's deals page often features discounts on courses that can complement practice on these platforms.
These courses are often structured around solving problems similar to those found on coding challenge platforms.
Community Forums for Peer Support
When embarking on a self-directed learning journey, especially for complex topics like Binary Search Trees, having access to community forums and peer support can be incredibly beneficial. Engaging with a community provides opportunities to ask questions, share solutions, discuss challenges, and learn from the experiences of others. This interaction can help overcome learning hurdles and maintain motivation.
Platforms like Stack Overflow are well-known for Q&A on specific programming problems, including those related to data structures. Subreddits such as r/learnprogramming, r/computerscience, or r/cscareerquestions often have discussions about learning resources, problem-solving strategies, and career advice. Many online courses also have their own dedicated forums or Discord channels where students can interact with each other and with instructors or teaching assistants.
Specific coding challenge websites like LeetCode or HackerRank usually have discussion sections for each problem, where users share their approaches, optimizations, and clarify doubts. GitHub, beyond hosting code, is also a place for discussion within project repositories, and many educational projects or open-source libraries related to data structures might have active communities.
When participating in these communities, it's helpful to:
- Be clear and specific when asking questions.
- Show what you've already tried or your current understanding.
- Be respectful and constructive in discussions.
- Contribute by helping others when you can; explaining a concept to someone else is a great way to solidify your own understanding.
For career changers or those new to tech, these communities can also provide valuable networking opportunities and insights into the industry. Learning in isolation can be challenging, but being part of a supportive community can make the journey more engaging and effective. You can also share useful resources you find on OpenCourser with your peers to help them in their learning paths.
While not forums themselves, these courses often have associated communities or encourage peer interaction.
Integration with Other Data Structure Concepts
Binary Search Trees do not exist in a vacuum; they are part of a larger ecosystem of data structures. A powerful self-directed learning strategy involves understanding how BSTs relate to, complement, or contrast with other data structures. This integrated understanding provides a more holistic view of data organization and algorithmic problem-solving.
Consider exploring connections such as:
- BSTs vs. Hash Tables: Both are used for efficient searching, insertion, and deletion. BSTs (especially balanced ones) provide O(log n) performance and maintain elements in sorted order, allowing for efficient range queries and ordered traversal. Hash tables offer O(1) average time complexity for these operations but do not typically maintain order. Understanding their trade-offs is crucial for choosing the right structure for a given task.
- BSTs vs. Sorted Arrays/Linked Lists: Compare the performance characteristics. Sorted arrays allow O(log n) search (using binary search) but have O(n) insertion/deletion. Linked lists have O(n) search but O(1) insertion/deletion if the position is known (though finding the position is O(n)). BSTs aim to provide logarithmic performance for all three.
- Heaps and Priority Queues: Heaps are another tree-based data structure, often implemented as binary trees (though not BSTs), specifically designed for efficient retrieval of the minimum or maximum element. Understanding heaps helps differentiate them from BSTs, which are optimized for general search and ordered traversal.
- Trees as a Basis for More Complex Structures: B-trees (used in databases) and k-d trees (used in spatial indexing) are more advanced tree structures that build upon some of the hierarchical and partitioning principles seen in BSTs.
- Graphs: As mentioned earlier, trees are a special type of graph. Understanding BSTs can be a stepping stone to learning about more general graph algorithms (DFS, BFS), which are widely applicable.
When learning a new data structure, actively try to compare its strengths, weaknesses, and typical use cases with those of structures you already know, including BSTs. This comparative approach helps in building a mental "toolkit" of data structures, enabling you to make more informed decisions when designing solutions to programming problems. Many comprehensive data structure courses on OpenCourser adopt this integrative approach.
These courses often cover a range of data structures, allowing for comparison and integration of concepts.
Books that cover multiple data structures are excellent for this integrative learning.
Exploring these related topics will naturally lead to an integrated understanding.
Future Trends and Challenges
The field of computer science is ever-evolving, and even foundational data structures like Binary Search Trees are subject to new research, applications, and challenges in the context of emerging technologies and changing computational landscapes.
BSTs in Machine Learning Pipelines
While traditional Binary Search Trees are primarily known for ordered data management, tree-based structures, in general, play a significant role in machine learning (ML). Decision trees, which are a core component of many ML algorithms, are a prime example. Although not strictly BSTs (as their splitting criteria are based on feature thresholds rather than a simple key order), they share the hierarchical, branching nature.
Ensemble methods like Random Forests and Gradient Boosted Trees leverage many individual decision trees to make more robust predictions. The efficiency of constructing, traversing, and pruning these trees is critical to the performance of the ML models. Research in ML might explore ways to optimize these tree-based algorithms, potentially drawing inspiration from advanced BST techniques for balancing or efficient searching, especially if the feature space has some inherent order or if specific types of queries on the model structure are needed.
Furthermore, some ML tasks involve searching through large, structured spaces of parameters or hypotheses. Specialized tree structures, potentially related to BSTs, could be used to manage these search spaces efficiently. For example, in reinforcement learning or game AI, search trees (like Monte Carlo Tree Search) are used to explore possible future states. While different from BSTs, the underlying principles of tree traversal and pruning are related. As ML models become more complex and datasets grow, the need for efficient underlying data structures, including innovative tree-based approaches, will likely continue.
For individuals interested in the intersection of data structures and machine learning, exploring Artificial Intelligence courses on OpenCourser can provide a broader context.
Courses on machine learning or advanced algorithms may touch upon the use of tree structures in AI.
record:40
Understanding the broader context of AI is useful.
Memory Optimization for Large-Scale Datasets
As datasets continue to grow exponentially, efficiently managing memory for data structures like Binary Search Trees becomes increasingly critical, especially when these structures need to operate on data that may not fit entirely within main memory. Traditional BST implementations, where each node is an object with pointers to children and data, can incur significant memory overhead due to pointer storage and object metadata.
Research and development in this area focus on several aspects:
- Compact Representations: Exploring ways to represent BSTs more compactly in memory, reducing pointer overhead. This might involve using implicit tree representations (e.g., storing a tree in an array like a binary heap, though this is harder for dynamic BSTs) or more sophisticated node encoding schemes.
- Cache-Efficient Layouts: Designing BSTs (and their variants like B-trees) whose memory layout minimizes cache misses during traversal and search operations. By arranging nodes that are likely to be accessed together in close proximity in memory, the number of slow main memory accesses can be reduced. This is crucial for performance on modern hardware.
- Disk-Based Trees (B-trees and variants): For datasets that are too large for RAM, B-trees and B+ trees are standard. These are not binary but multi-way search trees designed to minimize disk I/O by having a high branching factor, thus reducing tree height. Ongoing research might look into optimizing these for new storage technologies (like SSDs or persistent memory) or specific workload patterns.
- Memory Management Techniques: For dynamic trees with frequent insertions and deletions, efficient memory allocation and deallocation for nodes are important to prevent fragmentation and reduce overhead.
The challenge lies in balancing memory efficiency with the performance of tree operations and the complexity of implementation. Optimizing memory usage often involves intricate low-level considerations and a deep understanding of hardware architecture. These optimizations are vital for databases, file systems, and any application dealing with massive ordered datasets.
Courses on advanced data structures or systems programming may cover memory optimization techniques.
This book delves into the complexities of algorithms, including considerations for large datasets.
Quantum Computing Implications
The advent of quantum computing presents both exciting possibilities and new challenges for classical data structures and algorithms, including those based on Binary Search Trees. While quantum computers are not designed to simply speed up all classical computations, they excel at specific types of problems, and this could indirectly or directly impact how we think about searching and data organization.
One of the most famous quantum algorithms is Grover's algorithm, which can search an unsorted database of N items in O(√N) time, compared to O(N) classically. While BSTs are designed for sorted data (allowing O(log N) classical search), if data were unsorted or if the search problem didn't fit the BST model, Grover's algorithm offers a potential quantum speedup. However, the overhead of current quantum hardware and the specific nature of the "database" Grover's algorithm operates on mean it's not a straightforward replacement for classical search in all scenarios.
More directly, research is exploring how tree structures themselves might be implemented or utilized in quantum algorithms or on quantum hardware. For instance, quantum algorithms might traverse decision trees or other tree-like computational paths in novel ways, potentially leveraging quantum parallelism or interference. There's also work on "noisy tree data structures" which aims to develop tree operations that are robust to errors, a relevant concern in both probabilistic classical computation and fault-tolerant quantum computation.
The impact of quantum computing on classical data structures like BSTs is still an emerging area. It's unlikely that quantum computers will replace BSTs for everyday tasks on classical computers. Instead, the influence might be in solving very specific, complex problems where quantum speedups are possible, or in inspiring new classical algorithms based on insights from quantum information processing. For now, a strong understanding of classical data structures remains fundamental, even as the quantum era unfolds.
While specific courses on BSTs in quantum computing are rare and highly specialized, understanding the fundamentals of quantum computing is a first step.
Ethical Considerations in Algorithmic Efficiency
While discussions about Binary Search Trees often center on their technical efficiency (e.g., O(log n) vs. O(n)), it's increasingly important to consider the broader ethical implications that can arise from algorithmic efficiency and data structure choices, especially when these systems are used in decision-making processes that affect individuals.
Bias Amplification: If a BST or any data structure is used to store and quickly access data that itself reflects historical biases (e.g., biased datasets used in loan applications, hiring, or criminal justice), then the efficiency of the data structure can inadvertently help perpetuate or even amplify these biases by making it faster to act upon biased information. The data structure itself isn't biased, but its use within a biased system is a concern.
Access and Equity: The efficiency gains from structures like BSTs can lead to powerful applications. However, if access to these technologies or the benefits they provide is unevenly distributed, it can exacerbate existing inequalities. For example, systems optimized for speed might require significant computational resources, potentially disadvantaging those with less access to advanced hardware.
Transparency and Explainability: Complex data structures and algorithms, especially when part of larger AI systems, can sometimes become "black boxes," making it difficult to understand how a particular decision was reached. While BSTs are relatively transparent compared to deep learning models, the overall system they are part of might lack explainability, which is an ethical concern when individuals are adversely affected by automated decisions.
Purpose of Efficiency: Algorithmic efficiency is often pursued for performance and cost savings. However, it's important to ask "efficiency for what purpose?" If efficiency gains are used in ways that are socially harmful or discriminatory, then the technical achievement is overshadowed by the negative ethical impact. There's a growing call for "value-sensitive design" or "human-centered AI" that prioritizes human well-being and fairness alongside technical performance.
While a deep understanding of BSTs is a technical skill, developers and computer scientists also have a responsibility to consider the societal context in which their creations will be used. This involves being mindful of potential biases in data, striving for transparency, and advocating for the ethical application of technology. Learning resources like those on Social Sciences on OpenCourser can sometimes provide frameworks for thinking about these broader societal impacts.
Courses on AI ethics or technology and society often discuss these important considerations.
Frequently Asked Questions (Career Focus)
For those considering how knowledge of Binary Search Trees might impact their career, several common questions arise. Addressing these can help set realistic expectations and guide learning efforts.
Are BST questions common in technical interviews?
Yes, questions related to Binary Search Trees (and binary trees in general) are very common in technical interviews for software engineering roles, particularly for entry-level to mid-level positions. Companies like Google, Facebook (Meta), Amazon, Microsoft, and many others frequently use tree-based problems to assess a candidate's understanding of fundamental data structures, algorithms, recursion, and problem-solving skills.
Interview questions can range from basic (e.g., "Implement BST insertion," "Traverse a tree in-order") to more complex (e.g., "Validate if a tree is a BST," "Find the lowest common ancestor of two nodes," "Convert a sorted array to a balanced BST"). You might be asked to write code on a whiteboard or in a shared online editor, and you'll almost certainly be expected to analyze the time and space complexity of your solution.
The reason BSTs are popular interview topics is that they test multiple skills simultaneously: understanding of pointers or references, recursive thinking, algorithmic design, and attention to edge cases. Success in these questions often signals a solid computer science foundation. Therefore, thorough preparation on BST concepts and practicing a variety of related problems is highly recommended for anyone preparing for software engineering interviews.
Courses specifically designed for interview preparation usually dedicate significant time to tree-based questions.
How much BST knowledge is required for entry-level roles?
For entry-level software engineering roles, a solid foundational understanding of Binary Search Trees is generally expected. You don't necessarily need to be an expert capable of designing novel tree algorithms, but you should be comfortable with the core concepts and common operations.
Specifically, entry-level candidates should typically be able to:
- Explain what a BST is and its key properties (the ordering of nodes).
- Implement basic operations: search, insertion, and deletion (including handling cases for leaf nodes, nodes with one child, and nodes with two children, though the two-child deletion might be considered a more intermediate problem by some).
- Implement standard tree traversals: in-order, pre-order, and post-order, both recursively and ideally iteratively (at least for some traversals).
- Analyze the time and space complexity of these operations (O(log n) for balanced trees, O(n) worst-case for unbalanced).
- Understand the concept of tree balance and why it's important, even if not implementing self-balancing trees like AVL or Red-Black trees from scratch.
- Solve common interview problems related to BSTs, such as validating a BST or finding specific elements.
The depth of knowledge required can vary somewhat by company and specific role. However, since BST questions are common in interviews, demonstrating a good grasp of these fundamentals is crucial for making a positive impression and passing the technical screening. Online courses and coding practice platforms are excellent resources for building this level of knowledge. OpenCourser's Career Development section may also offer broader advice on preparing for technical roles.
These courses cover the fundamental BST knowledge typically expected for entry-level positions.
Basic understanding of tree structures is a good starting point.
Can BST expertise lead to leadership positions?
While expertise in Binary Search Trees alone is unlikely to be the sole factor for promotion to a leadership position, a deep understanding of fundamental data structures and algorithms, of which BSTs are a key part, contributes significantly to the technical competence and problem-solving abilities expected of technical leaders.
Leadership roles in software engineering (e.g., Tech Lead, Engineering Manager, Architect) often require the ability to:
- Make sound technical decisions regarding system design and architecture, which includes choosing appropriate data structures and algorithms for optimal performance, scalability, and maintainability.
- Mentor and guide junior engineers, helping them develop their own understanding of fundamental concepts like BSTs.
- Troubleshoot complex performance issues, which may involve analyzing how data is structured and accessed.
- Evaluate new technologies and approaches, understanding their underlying algorithmic principles.
- Communicate complex technical concepts clearly to both technical and non-technical stakeholders.
A strong grasp of fundamentals like BSTs builds credibility and demonstrates a commitment to technical excellence. It allows leaders to engage in deep technical discussions, ask insightful questions, and command the respect of their teams. While soft skills, communication, project management, and strategic thinking become increasingly important in leadership, a solid technical foundation remains crucial, especially in technology-driven organizations. Thus, continuous learning and mastery of core computer science principles, including data structures like BSTs, support long-term career growth and the potential to move into leadership roles.
Advanced courses can help deepen the technical expertise that supports leadership aspirations.
Developing a broad understanding of computer science is also key.
Industries with highest BST adoption rates
Binary Search Trees and their variants (like B-trees, Red-Black trees) are fundamental data structures, so their principles are applied across a wide range of industries where efficient management and retrieval of ordered data are important. It's less about specific industries "adopting BSTs" directly, and more about industries relying on software and systems that internally use these structures.
Some key areas include:
- Software Development (across all industries): Any company developing software that requires efficient searching, sorting, or storage of ordered data may use libraries or implement custom solutions that leverage BST principles. This includes tech giants, financial services, healthcare, e-commerce, and more. Standard library collections like `std::map` in C++ or `TreeMap` in Java, which are often based on balanced BSTs, are widely used.
- Database Technology: The entire database industry relies heavily on tree-based indexing structures (often B-trees or B+ trees, which are relatives of BSTs optimized for disk) to ensure fast query performance. This is fundamental to relational databases, NoSQL databases with secondary indexes, and data warehousing solutions.
- Operating Systems: File systems use hierarchical structures (trees) for organization, and some internal OS components might use tree-like data structures for managing resources or processes.
- Networking Equipment: Routers and other networking devices may use specialized tree structures (like tries or Patricia trees) for efficient IP address lookup and packet forwarding.
- Game Development: For spatial indexing, visibility determination, and collision detection, game engines often use tree structures like BSP trees or k-d trees.
- Compilers and Interpreters: These tools use Abstract Syntax Trees (ASTs) to represent the structure of code during parsing and analysis.
Essentially, any industry that leverages sophisticated software systems for data management, search, or complex computations will indirectly be using the principles embodied by BSTs. The U.S. Bureau of Labor Statistics projects strong growth for software developers across various sectors, highlighting the broad applicability of these foundational skills.
Understanding the breadth of software development can provide insight into where these skills are applied.
Freelancing Opportunities Involving BST Implementations
Direct freelancing opportunities that *solely* require implementing a basic Binary Search Tree are likely to be rare. BSTs are a foundational concept, and standard libraries in most programming languages already provide robust, well-tested implementations of balanced BSTs (like `std::map` in C++ or `TreeMap` in Java). Clients are more likely to use these existing solutions rather than commission a custom BST implementation from scratch unless there's a very specific, niche requirement.
However, freelancing opportunities where a strong understanding of BSTs (and data structures/algorithms in general) is beneficial or implicitly required are more common. These could include:
- Custom Software Development: Building applications that require efficient data management, searching, and sorting. While you might use library implementations of tree-based collections, knowing how they work helps in choosing the right tools and optimizing their use.
- Performance Optimization: Clients may need help optimizing existing software that is slow due to inefficient data handling. Understanding data structures can help identify bottlenecks and suggest better approaches.
- Algorithm Design and Implementation: For specialized problems, a client might need a custom algorithm developed, which could involve tree-based logic or other advanced data structures.
- Tutoring or Technical Training: Freelancers with strong expertise in data structures and algorithms can offer tutoring services to students or training to corporate teams.
- Technical Writing: Creating documentation, articles, or educational content related to data structures and algorithms.
For freelancers, showcasing a portfolio of projects that demonstrate strong problem-solving skills and an understanding of efficient algorithm design (which includes knowledge of structures like BSTs) is more impactful than just listing "BST implementation" as a skill. Focusing on broader skills like "backend development," "database optimization," or "Python/Java/C++ development" while having a solid grasp of underlying computer science fundamentals will open up more freelancing doors.
Building a strong overall software development skillset is key for freelancing.
Consider exploring careers that often have freelance components.
BSTs vs. Hash Tables: Career Application Differences
Binary Search Trees (specifically balanced ones) and Hash Tables are two of the most fundamental data structures used for storing and retrieving data, but they have different characteristics and are suited for different types of applications. Understanding these differences is crucial for software developers when making design choices.
Binary Search Trees (Balanced):
- Performance: Offer O(log n) average and worst-case time complexity for search, insertion, and deletion.
- Ordered Data: A key advantage is that BSTs maintain elements in sorted order. This allows for efficient in-order traversal to retrieve all elements sorted, and also enables efficient range queries (e.g., find all elements between X and Y) and finding the next smallest/largest element.
- Use Cases: Suitable when ordered traversal, range queries, or finding successor/predecessor elements are important, in addition to efficient search/insert/delete. Examples include implementing sorted sets or maps, some types of database indexing where order matters.
Hash Tables (Hash Maps):
- Performance: Offer O(1) average time complexity for search, insertion, and deletion. However, the worst-case complexity can be O(n) if many collisions occur and are not handled well (though good hash functions and collision resolution strategies make this rare in practice).
- Unordered Data: Hash tables do not typically maintain elements in any specific order. Iterating through a hash table will usually yield elements in an arbitrary or unpredictable sequence.
- Use Cases: Ideal when the primary requirement is extremely fast lookups, insertions, and deletions, and order is not important. Examples include implementing dictionaries, caches, symbol tables in compilers, or any scenario where quick key-value mapping is needed.
Career Application Differences:
A software engineer will frequently encounter situations where they need to choose between a tree-based structure (like a balanced BST, often via a library's `map` or `set`) and a hash-based structure (via a library's `hash_map`, `unordered_map`, or `dictionary`).
- If the application requires iterating over elements in sorted order, or performing operations based on ordering (like finding all items in a price range), a BST-based structure is generally preferred.
- If the primary goal is the absolute fastest possible average-case lookup, and order doesn't matter, a hash table is usually the go-to choice.
In technical interviews, you might be asked to compare these two structures or to choose the most appropriate one for a given problem scenario, justifying your choice based on their performance characteristics and features. Both are fundamental, and proficiency with both is expected for most software development roles.
Understanding both data structures is crucial. These courses cover general data structures, often including both trees and hash tables.
This book offers a comprehensive comparison of various data structures.
Explain Like I'm 5: Binary Search Trees
Imagine you have a big box of toy blocks, and each block has a number on it. You want to find a specific block, say the one with the number 15, as quickly as possible. If the blocks are all jumbled up, you might have to look at every single block until you find it. That could take a long time!
A Binary Search Tree is like a super organized way to arrange these blocks. Think of it like this:
You pick one block to be the "boss" block (this is called the root). Let's say the boss block has the number 20 on it.
Now, for any new block you get:
- If its number is smaller than the boss block's number (20), you put it in a pile to the left of the boss.
- If its number is bigger than the boss block's number (20), you put it in a pile to the right of the boss.
You do this for every block in those piles too! So, if you put a block with number 10 in the "left" pile, and then you get a block with number 5, since 5 is smaller than 10, it goes to the left of the 10 block. If you get a block with 17, it's bigger than 10, so it goes to the right of the 10 block (but still in the main "left of 20" area).
So, it looks like a branching tree:
20
/
10 30
/ /
5 17 25 35
Now, why is this helpful for finding block number 15?
1. You start at the boss block (20).
2. Is 15 smaller or bigger than 20? It's smaller. So, you know it MUST be in the left pile (if it's there at all). You can ignore the whole right pile!
3. Now you look at the boss of the left pile (10). Is 15 smaller or bigger than 10? It's bigger. So you go to the right of 10.
4. The block to the right of 10 is 17. Is 15 smaller or bigger than 17? It's smaller. So you go to the left of 17.
5. Uh oh! There's no block to the left of 17 in our example. That means block 15 isn't in our tree!
If block 15 was there (say, to the left of 17), we would have found it very quickly by always choosing left or right, and ignoring half the blocks at each step. That's much faster than looking at every single block one by one!
So, a Binary Search Tree just helps you search for things (like numbers, or even words sorted alphabetically) really fast by always keeping them in this special "smaller to the left, bigger to the right" order.
For young learners or those completely new to programming, grasping this simple analogy can be the first step towards understanding more complex data structures. Resources on OpenCourser's K-12 Subjects page might offer more introductory materials to computer science concepts.
These introductory courses can help build a visual and conceptual understanding of tree structures.
Conclusion
Binary Search Trees are a cornerstone data structure in the world of computer science. Their elegant, ordered nature provides an efficient way to manage and query data, forming the bedrock for numerous applications, from database indexing to the internal workings of software libraries. Understanding their properties, operations, and the critical concept of balance is essential for anyone aspiring to a career in software development, data science, or any field that involves algorithmic thinking.
The journey to mastering BSTs, like any worthwhile endeavor in computer science, requires dedication and practice. Whether you are pursuing a formal education, are in the midst of a career transition, or are simply a curious lifelong learner, the resources available today, including a vast array of online courses and supportive communities, make this knowledge more accessible than ever. By engaging with the material, working through problems, and ideally, building projects, you can develop a robust understanding that will serve you well in technical interviews and in your career.
While the path may present challenges, the ability to effectively wield data structures like BSTs is a powerful skill that opens doors to solving complex problems and contributing to innovative technological solutions. We encourage you to explore the courses and resources available on OpenCourser to guide your learning journey and help you achieve your professional and personal development goals in this exciting field. Remember that a solid grasp of fundamentals is the key to unlocking more advanced concepts and, ultimately, to a fulfilling and impactful career in technology.