Monte Carlo simulations
In-Depth Guide to Monte Carlo Simulations
Monte Carlo simulations are a class of computational algorithms that rely on repeated random sampling to obtain numerical results. Essentially, they use randomness to solve problems that might be deterministic in principle. This technique is particularly valuable for understanding the impact of risk and uncertainty in prediction and forecasting models. Imagine trying to predict the outcome of a complex system with many interacting, uncertain parts; a Monte Carlo simulation allows you to explore a wide range of possibilities and their likelihoods.
The power of Monte Carlo simulations lies in their ability to model scenarios with inherent randomness or a high degree of uncertainty. This makes them exciting tools in fields ranging from finance, where they help assess investment risks and price complex derivatives, to engineering, where they can model system reliability or project timelines. The ability to quantify uncertainty and provide a spectrum of potential outcomes, rather than a single deterministic prediction, is a key aspect that many find engaging. Furthermore, the increasing integration of Monte Carlo methods with artificial intelligence and machine learning opens up new frontiers for sophisticated modeling and decision-making.
Introduction to Monte Carlo Simulations
At its core, a Monte Carlo simulation is a mathematical technique used to estimate the possible outcomes of an uncertain event or process. Instead of relying on a single set of inputs, it involves running a model numerous times, each time with a different set of random inputs drawn from probability distributions that represent the uncertainty in those inputs. By analyzing the collection of outcomes from these multiple runs, one can understand the range of possible results and the probability of each.
This approach is fundamentally different from deterministic modeling, where you input specific values and get a single, fixed output. Monte Carlo simulations embrace uncertainty, providing a more realistic picture when dealing with variables that are not perfectly predictable. This makes them incredibly versatile and widely used across various disciplines.
What are Monte Carlo Simulations?
A Monte Carlo simulation is a computational technique that uses repeated random sampling to generate numerical results. Think of it as conducting many "what-if" experiments on a computer. Instead of using fixed numbers as inputs for a model, you define a range of possible values for any input that has inherent uncertainty. The simulation then randomly selects values from these ranges, runs the model, and records the outcome. This process is repeated many times—often thousands or even millions—to build up a distribution of possible results. The name "Monte Carlo" itself, coined during the Manhattan Project, alludes to the famous casino in Monaco, reflecting the central role of chance and random outcomes in this modeling technique.
The core idea is that by running enough simulations, the collection of outcomes will approximate the true probability distribution of the results you are trying to predict. This allows you to not only estimate an average outcome but also to understand the likelihood of extreme outcomes, the range of possibilities, and the overall risk involved. It's a powerful way to quantify the impact of uncertainty.
These simulations are particularly useful when dealing with complex systems or problems where an analytical solution (a direct mathematical formula) is difficult or impossible to obtain. By breaking down the problem into a series of probabilistic steps and running many iterations, insights can be gained that would otherwise be hidden.
A Brief History
The conceptual underpinnings of using randomness to solve problems date back further, with early variants like the Buffon's needle problem in the 18th century. However, the modern development of Monte Carlo methods is largely credited to Stanislaw Ulam, a mathematician working on the Manhattan Project at Los Alamos National Laboratory in the 1940s. Faced with the challenge of modeling neutron diffusion, which was too complex for existing analytical methods, Ulam conceived of using repeated random sampling. He discussed this idea with John von Neumann, another brilliant mind on the project, and together they developed the computational framework.
The name "Monte Carlo" was suggested by Nicholas Metropolis, a colleague of Ulam and von Neumann, as a code name for the secret work, referencing the Monte Carlo Casino in Monaco where Ulam's uncle often gambled. The first fully automated Monte Carlo calculations were performed on the ENIAC computer in 1948 to model a fission weapon core. Following World War II, the methods were further developed for the hydrogen bomb project and subsequently became popularized in fields like physics, physical chemistry, and operations research, with organizations like the Rand Corporation playing a significant role in their dissemination.
Since those early days, the applications of Monte Carlo simulations have expanded dramatically, driven by the increasing availability of computational power. They are now indispensable tools in diverse areas such as finance, engineering, supply chain management, environmental science, drug development, and even artificial intelligence.
For those interested in foundational knowledge, these courses can help build a solid understanding of the probabilistic and computational concepts that underpin Monte Carlo simulations.
And for a deeper dive into the methods themselves, these books are considered valuable resources.
Key Applications Across Industries
Monte Carlo simulations have found a vast array of applications across numerous industries due to their ability to model uncertainty and variability. In finance, they are extensively used for tasks like portfolio risk assessment, option pricing, and stress testing financial models. For instance, financial analysts use Monte Carlo methods to simulate thousands of potential market scenarios to understand the range of possible returns for an investment portfolio and the likelihood of losses. They are also crucial in pricing complex financial derivatives where analytical formulas are unavailable.
In engineering and project management, these simulations help estimate project completion times and costs, considering uncertainties in task durations, resource availability, and potential disruptions. They can identify critical paths and quantify the probability of meeting deadlines or budgets. Telecom companies use them to assess network performance under various scenarios to optimize network design. In manufacturing, Monte Carlo methods can model production lines to identify bottlenecks and improve efficiency, considering variabilities in machine uptime and processing times.
Beyond business and engineering, Monte Carlo simulations are vital in many scientific disciplines. In physics, they model complex systems with many interacting particles, such as in studies of fluid dynamics or material properties. Meteorologists and environmental scientists use them for weather forecasting and climate modeling, incorporating the inherent randomness of atmospheric processes. In drug development and bioinformatics, they can simulate molecular interactions or predict the efficacy of new treatments. Even in fields like artificial intelligence, Monte Carlo Tree Search is a key algorithm in game playing programs.
The following courses offer insights into some of these diverse applications.
To further explore the breadth of applications, consider these topics.
Advantages Over Deterministic Methods
Monte Carlo simulations offer several significant advantages over deterministic methods, especially when dealing with uncertainty and complex systems. Deterministic models use fixed, single-point inputs and produce a single-point output. While simple, this approach often fails to capture the real-world variability and risk inherent in many problems.
One primary advantage is probabilistic results. Instead of a single outcome, Monte Carlo simulations generate a distribution of possible outcomes and their associated probabilities. This gives decision-makers a much richer understanding of the potential upsides and downsides of a particular course of action. For example, instead of just an average project cost, you get a range of possible costs and the likelihood of exceeding a certain budget.
Another key benefit is enhanced risk assessment. By modeling the full range of potential outcomes, Monte Carlo methods allow for a more thorough identification and quantification of risks. This enables better-informed decisions about risk mitigation strategies and contingency planning. They also facilitate sensitivity analysis, making it easier to identify which input variables have the most significant impact on the outcome. This helps focus attention on the most critical factors.
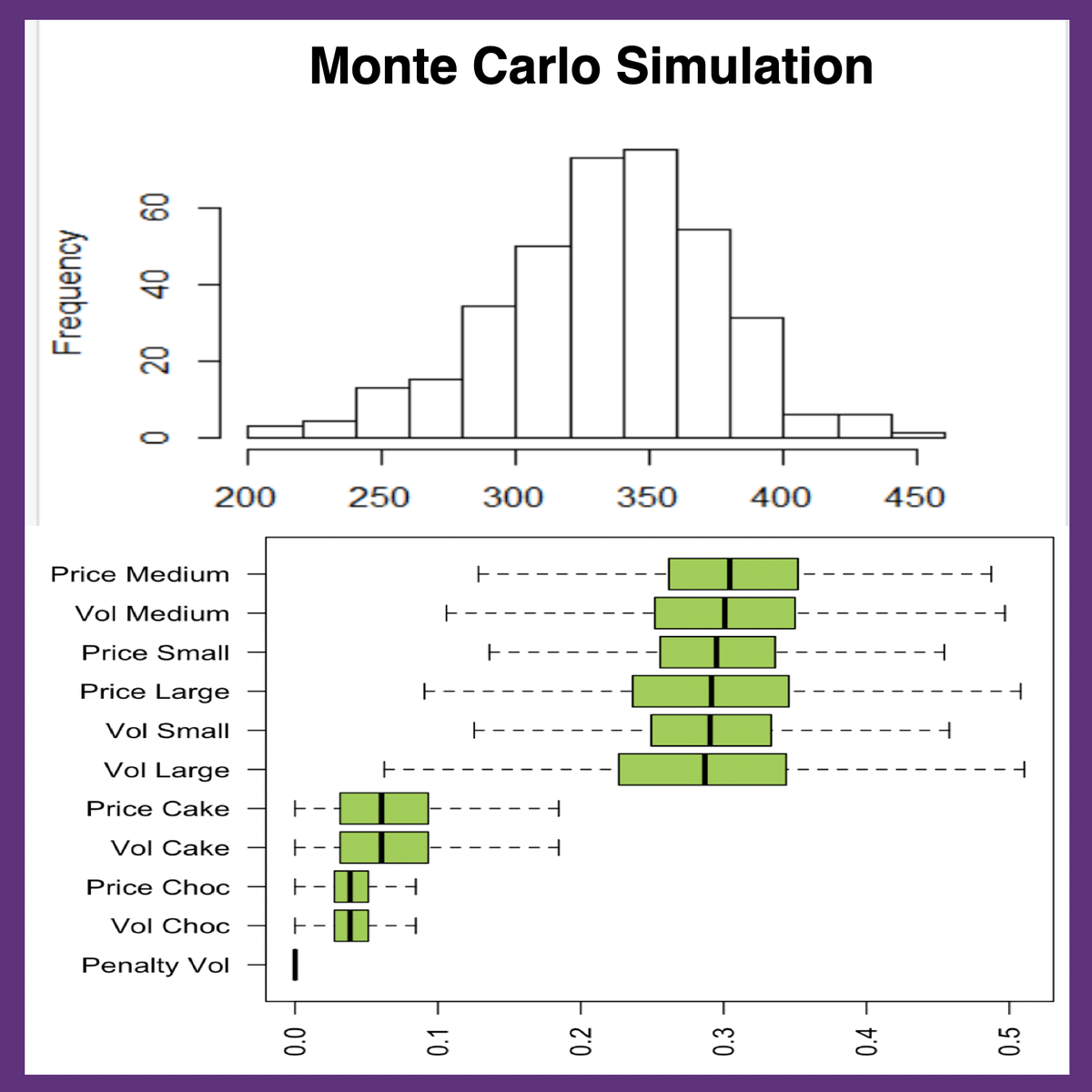
Furthermore, Monte Carlo simulations can handle complex, non-linear relationships and interdependencies between variables that are difficult to model with deterministic approaches. They are also generally easier to explain and visualize, as the concept of running many scenarios is intuitive, and the results can often be presented in graphical forms like histograms. While deterministic methods might give you an answer like "the project will take 10 months," a Monte Carlo simulation might tell you "there's a 60% chance the project will take between 9 and 11 months, a 15% chance it will take less than 9 months, and a 25% chance it will take more than 11 months." This level of insight is invaluable for robust decision-making in uncertain environments.
Core Principles of Monte Carlo Simulations
Understanding Monte Carlo simulations requires grasping a few fundamental concepts. These principles are the bedrock upon which the power and versatility of this technique are built. From the way randomness is harnessed to how we gain confidence in the results, these core ideas are essential for anyone looking to apply or interpret Monte Carlo methods effectively.
At its heart, the method relies on the idea that repeated random sampling can reveal the underlying probabilistic nature of a complex system. This involves not just generating random numbers, but doing so in a way that accurately reflects the uncertainties of the real-world variables being modeled.
Random Sampling and Probability Distributions
The foundation of any Monte Carlo simulation is random sampling from probability distributions. Instead of assuming a single, fixed value for an uncertain input variable, we define it by a probability distribution that describes the likelihood of each possible value that variable might take. For example, if we're modeling project task duration, we might use a triangular distribution (defined by a minimum, most likely, and maximum time) or a normal distribution (bell curve) if we have a good estimate of the average time and its variability.
The simulation then repeatedly draws random samples for each uncertain input variable according to its specified probability distribution. If a model has multiple uncertain inputs, a set of random values (one for each input) is drawn in each iteration. This process of generating random inputs is crucial; the quality and appropriateness of the chosen probability distributions directly impact the validity of the simulation results. Common distributions used include the normal, uniform, lognormal, triangular, binomial, and Poisson distributions, each suited to different types of uncertainty.
The use of random numbers is what gives the method its name, but it's important to note that computers use pseudo-random number generators – algorithms that produce sequences of numbers that appear random but are actually deterministic if the starting point (the "seed") is known. For most applications, these are sufficient, though for some highly sensitive areas like cryptography, true random number generation might be necessary.
Understanding probability is key. These resources provide a good starting point.
Law of Large Numbers Justification
The mathematical underpinning that makes Monte Carlo simulations work is the Law of Large Numbers (LLN). In simple terms, the LLN states that as the number of trials or observations in a random experiment increases, the average of the results obtained from those trials will tend to get closer to the true expected value of the experiment.
In the context of Monte Carlo simulations, each run of the model with a new set of random inputs can be considered a "trial." The output of that single run is one observation. As we perform more and more runs (i.e., increase the number of samples), the average of all the output values from these runs will converge towards the true mean or expected outcome of the system being modeled. This is why simulations are typically run thousands or even millions of times – to ensure that the sample average is a reliable estimate of the true underlying average.
The LLN provides the theoretical justification for why we can trust the results of a well-constructed Monte Carlo simulation, provided enough iterations are performed. It assures us that by repeatedly sampling and averaging, we can approximate complex probabilistic outcomes with increasing accuracy. It's the principle that allows us to move from the randomness of individual samples to a stable and meaningful aggregate result.
This principle is fundamental not just to Monte Carlo methods but to much of statistical inference. Learning more about it can deepen one's understanding of how we draw conclusions from data.
Convergence and Error Estimation
While the Law of Large Numbers tells us that the average result from a Monte Carlo simulation will approach the true expected value as the number of samples (N) increases, a practical question is: how many samples are enough? This brings us to the concepts of convergence and error estimation. Convergence refers to how the simulation's output (e.g., the estimated mean) stabilizes and gets closer to a specific value as N grows.
The accuracy of a Monte Carlo estimate is often related to its standard error, which typically decreases in proportion to the square root of N (i.e., 1/√N). This means that to halve the error, you generally need to quadruple the number of simulation runs. Understanding this relationship is crucial for balancing computational cost with desired accuracy. For example, if 10,000 runs give you an acceptable level of error, reducing that error by a factor of 10 would require 1,000,000 runs (100 times more samples).
Several methods can be used to assess convergence and estimate error. One common approach is to monitor the running average or other statistics of interest as N increases. When these statistics stop changing significantly with additional simulations, it suggests convergence. More formally, the Central Limit Theorem often applies, which states that the distribution of the sample mean (from many simulations) will tend to be normally distributed around the true mean. This allows for the calculation of confidence intervals around the estimated result, providing a quantitative measure of the uncertainty associated with the Monte Carlo estimate. For example, you might conclude with 95% confidence that the true mean lies within a certain range.
Careful consideration of convergence and error is vital to ensure that the results of a Monte Carlo simulation are reliable and that the computational effort is justified.
Variance Reduction Techniques
Because the standard error of a Monte Carlo estimate typically decreases with 1/√N, achieving high accuracy can sometimes require a very large number of simulation runs, leading to significant computational cost. Variance reduction techniques (VRTs) are methods designed to improve the efficiency of Monte Carlo simulations by reducing the variance of the output estimator for a given number of samples, or achieving the same level of accuracy with fewer samples.
There are many types of VRTs. Some common examples include:
- Antithetic Variates: This involves introducing negative correlation between pairs of simulation runs. If one run uses a random number u, the next might use 1-u. This can help to cancel out some of the random fluctuations.
- Control Variates: If there's another, similar quantity whose expected value is known analytically and which is correlated with the quantity being estimated, this known quantity can be used to "control" or adjust the estimate, reducing its variance.
- Importance Sampling: This technique involves modifying the sampling distribution to focus more on regions of the input space that contribute most to the quantity being estimated. Results are then weighted to correct for this biased sampling. This can be very powerful if good importance functions are known.
- Stratified Sampling: The input domain is divided into several sub-domains ("strata"), and a fixed number of samples are drawn from each stratum. This ensures that all parts of the input space are adequately represented, which can be more efficient than simple random sampling, especially if some strata are more important or have higher variance.
- Quasi-Monte Carlo Methods: Instead of using pseudo-random numbers, these methods use low-discrepancy sequences (e.g., Sobol or Halton sequences). These sequences are designed to fill the sample space more evenly than random numbers, which can lead to faster convergence for certain types of problems, particularly numerical integration.
The choice of VRT depends on the specific problem. While they can significantly enhance simulation efficiency, they can also add complexity to the implementation. Nevertheless, for computationally intensive simulations, the benefits of variance reduction often outweigh the added effort.
Monte Carlo Simulations in Financial Analysis
The field of finance is one of the most prominent and impactful areas where Monte Carlo simulations are applied. Given the inherent uncertainties in financial markets – fluctuating asset prices, changing interest rates, unpredictable economic events – the ability of Monte Carlo methods to model and quantify this uncertainty is invaluable. Financial professionals rely on these simulations to make more informed decisions about investments, risk management, and strategic planning.
From valuing complex financial instruments to assessing the long-term viability of retirement plans, Monte Carlo techniques provide a framework for navigating the complexities of financial forecasting and risk. They allow analysts to move beyond simple, deterministic projections and explore a richer landscape of potential financial futures.
These courses provide practical insights into financial applications.
For those looking to delve deeper into the theory and application of Monte Carlo methods in finance, these books are highly recommended.
You may also wish to explore these related topics to broaden your understanding of the financial context.
Portfolio Risk Assessment
One of the primary uses of Monte Carlo simulations in finance is for portfolio risk assessment. An investment portfolio typically consists of various assets (stocks, bonds, commodities, etc.), each with its own risk and return characteristics and correlations with other assets. Monte Carlo simulations allow analysts to model the potential future performance of the entire portfolio by simulating the price behavior of its constituent assets.
The process usually involves defining probability distributions for the expected returns, volatilities, and correlations of the assets in the portfolio. The simulation then generates thousands or millions of possible future market scenarios, and for each scenario, it calculates the resulting portfolio value. This generates a distribution of potential portfolio returns, from which various risk metrics can be derived, such as Value at Risk (VaR) – the maximum potential loss over a specific time horizon at a given confidence level – or Conditional Value at Risk (CVaR).
This approach helps investors and portfolio managers understand the range of possible outcomes, the likelihood of achieving certain return targets, and the potential for significant losses. It's a powerful tool for asset allocation decisions, helping to construct portfolios that align with an investor's risk tolerance and financial goals. According to Ortec Finance, while traditional Monte Carlo simulations are an improvement over simplistic straight-line return assumptions, more sophisticated models are needed to account for events like market crises.
Option Pricing Models
Monte Carlo simulations are extensively used for pricing financial options, particularly those with complex features or multiple underlying assets, where analytical solutions like the Black-Scholes formula may not be applicable or easy to derive. An option's value depends on the future price of its underlying asset(s). Monte Carlo methods simulate a large number of possible price paths for the underlying asset(s) until the option's expiration date.
For each simulated path, the payoff of the option at expiration is calculated. For example, for a European call option, the payoff is the maximum of zero or the underlying asset price minus the strike price. These individual payoffs are then discounted back to the present value using a risk-free interest rate. The average of all these discounted present values across all simulated paths provides an estimate of the option's fair price.
This technique is very flexible and can handle various complexities, such as path-dependent options (e.g., Asian options, where the payoff depends on the average price over a period) or options on multiple assets (e.g., basket options). While powerful, the accuracy depends on the number of simulated paths and the appropriateness of the model used for the underlying asset's price movements. Variance reduction techniques are often employed to improve efficiency in option pricing simulations.
Stress Testing Scenarios
Stress testing is a critical risk management practice in finance, designed to assess how well a financial institution or an investment portfolio can withstand severe but plausible adverse economic scenarios. Monte Carlo simulations play a vital role in this process by allowing analysts to model the impact of these extreme events. Instead of just looking at historical data, which may not include precedents for all potential future crises, simulations can create hypothetical stress scenarios.
In a Monte Carlo-based stress test, specific adverse conditions are defined for key economic variables – such as a sharp decline in stock markets, a spike in interest rates, a credit crunch, or a severe recession. The simulation then models how these stressed inputs would affect the values of assets, liabilities, and overall financial health. This can involve complex interactions between different risk factors.
The results of these stress tests help financial institutions understand their vulnerabilities, assess the adequacy of their capital reserves, and develop contingency plans. Regulators also often require banks and other financial entities to conduct regular stress tests to ensure financial stability. Monte Carlo simulations provide a flexible and powerful framework for exploring a wide range of "what-if" scenarios under stressed conditions, offering insights beyond what traditional historical analysis can provide.
Regulatory Capital Requirements
Financial regulators globally impose capital requirements on banks and other financial institutions to ensure they have sufficient financial resources to absorb potential losses and remain solvent, even during periods of financial stress. Monte Carlo simulations are increasingly used by both financial institutions and regulators in the context of determining and assessing these capital requirements. For example, under frameworks like Basel III, banks often use internal models, which can include Monte Carlo simulations, to calculate their risk-weighted assets and, consequently, their minimum required capital for credit risk, market risk, and operational risk.
For market risk, simulations can model the potential losses in a bank's trading portfolio under various market scenarios. For credit risk, they can estimate potential losses from defaults in loan portfolios, considering factors like borrower creditworthiness and economic conditions. Operational risk, which arises from failures in internal processes, people, and systems, or from external events, can also be modeled using Monte Carlo methods to estimate the likelihood and impact of various operational loss events.
By providing a probabilistic assessment of potential losses, Monte Carlo simulations help institutions make more risk-informed decisions about their capital levels. Regulators, in turn, may use these methods or review the models used by institutions to ensure they are robust and that capital levels are adequate to maintain the stability of the financial system. The sophistication of these models allows for a more granular and forward-looking approach to capital adequacy than simpler, standardized approaches.
Formal Education Pathways
For individuals aspiring to specialize in areas that heavily utilize Monte Carlo simulations, a strong formal education provides an essential foundation. This typically involves a rigorous curriculum in quantitative disciplines, equipping students with the mathematical, statistical, and computational skills necessary to develop, implement, and interpret these sophisticated models. While self-study can supplement this, a structured academic program often offers a more comprehensive and in-depth understanding.
The journey usually begins at the undergraduate level with foundational courses and can extend to graduate and doctoral studies for those seeking advanced research or highly specialized roles. The interdisciplinary nature of Monte Carlo applications means that pathways can emerge from various quantitative fields.
Undergraduate Mathematics/Statistics Prerequisites
A solid undergraduate education in mathematics and/or statistics is the cornerstone for anyone wishing to delve deeply into Monte Carlo simulations. Key prerequisite subjects include a strong grounding in calculus (differential and integral), as it forms the basis for understanding continuous probability distributions and many optimization techniques. Linear algebra is also crucial, especially for handling multi-dimensional problems and understanding the mechanics of many computational algorithms.
Of paramount importance is a thorough understanding of probability theory. This includes concepts like random variables, probability distributions (discrete and continuous), expected values, variance, covariance, and conditional probability. Closely related is mathematical statistics, which covers topics such as estimation theory (point and interval estimation), hypothesis testing, and regression analysis. These subjects provide the theoretical framework for understanding how to model uncertainty and draw inferences from random samples, which are central to Monte Carlo methods.
Many undergraduate programs in mathematics, statistics, physics, engineering, economics, or computer science will offer courses covering these essential areas. Students should aim for a curriculum that not only teaches the theory but also provides opportunities to apply these concepts to problem-solving, ideally with some exposure to computational tools.
These courses can help build a strong mathematical and statistical foundation.
Graduate-Level Computational Methods Courses
At the graduate level, students can pursue more specialized courses in computational methods that directly involve or heavily utilize Monte Carlo simulations. Master's or PhD programs in fields like computational science, financial engineering, operations research, data science, applied mathematics, or statistics often feature such courses. These courses build upon the undergraduate prerequisites and delve into the advanced theory and practical implementation of simulation techniques.
Topics covered might include advanced probability theory, stochastic processes (like Markov chains, which are fundamental to Markov Chain Monte Carlo methods), random number generation techniques, the detailed study of various Monte Carlo algorithms (e.g., Metropolis-Hastings, Gibbs sampling), variance reduction techniques, and the application of these methods to specific domains like physics, finance, or engineering. Students will typically learn how to design simulation experiments, analyze their output, assess convergence and error, and implement these methods using programming languages such as Python, R, or C++.
Many programs also emphasize the mathematical underpinnings of why these methods work, including proofs of convergence and error bounds. Practical coursework often involves tackling complex, real-world or research-level problems, providing students with hands-on experience in applying Monte Carlo simulations to solve challenging questions.
This advanced course delves into computational thinking and data science, often incorporating simulation concepts.
For those aiming for a deep theoretical understanding, advanced texts are indispensable.
PhD Research Applications
For those pursuing a Doctor of Philosophy (PhD), Monte Carlo simulations often become a critical research tool or even the central focus of their dissertation. PhD research frequently involves pushing the boundaries of knowledge, and Monte Carlo methods are invaluable for tackling problems that are analytically intractable or involve high degrees of complexity and uncertainty. Researchers in a vast array of scientific and engineering disciplines employ these simulations.
In computational physics or chemistry, PhD students might use Monte Carlo simulations to model the behavior of materials at the atomic level, simulate quantum systems, or study complex fluid dynamics. In financial mathematics, doctoral research could involve developing new Monte Carlo techniques for pricing exotic derivatives, managing portfolio risk under complex market models, or assessing systemic risk. Statisticians might work on advancing the theory of Monte Carlo methods themselves, such as developing more efficient sampling algorithms, new variance reduction techniques, or methods for high-dimensional problems.
PhD candidates often need to not only apply existing Monte Carlo methods but also to innovate, perhaps by tailoring techniques to novel problems, combining them with other computational approaches (like machine learning), or developing entirely new simulation frameworks. The rigorous training in mathematics, statistics, and computation during doctoral studies provides the necessary skills for such advanced research applications. The ability to critically evaluate the assumptions, limitations, and accuracy of simulation results is also a key outcome of PhD-level work.
Interdisciplinary Programs
The power and versatility of Monte Carlo simulations have led to their widespread adoption across many fields, fostering the growth of interdisciplinary academic programs that heavily feature these methods. These programs recognize that many modern scientific and engineering challenges require expertise that spans traditional disciplinary boundaries. Examples include computational science and engineering, quantitative finance, bioinformatics, data science, and systems biology.
In a computational science program, students might learn to apply Monte Carlo methods to simulate physical phenomena, chemical reactions, or engineering systems. Quantitative finance programs heavily emphasize Monte Carlo techniques for risk management, derivative pricing, and algorithmic trading. Bioinformatics and computational biology programs use simulations to model biological systems, from protein folding to population genetics. Data science programs, while broad, often include advanced simulation and resampling techniques (like bootstrap methods, which have roots in Monte Carlo ideas) for model validation and uncertainty quantification.
These interdisciplinary programs typically offer a curriculum that blends core mathematical and statistical theory with computational skills and domain-specific knowledge. Students gain experience in applying Monte Carlo simulations to problems relevant to their chosen interdisciplinary area, preparing them for careers that require a sophisticated, quantitative approach to problem-solving in complex, uncertain environments.
Courses in specialized areas often touch upon or heavily utilize simulation techniques.
Online Learning and Self-Directed Study
For those looking to acquire skills in Monte Carlo simulations outside traditional academic pathways, or to supplement formal education, online learning and self-directed study offer flexible and accessible alternatives. The wealth of resources available online, from comprehensive courses to specialized tutorials and open-source software, empowers motivated individuals to learn at their own pace and tailor their studies to specific interests or career goals. This path requires discipline and a proactive approach to learning.
Whether you are a career changer aiming to enter a quantitative field, a professional looking to upskill, or a student seeking additional knowledge, the digital landscape provides ample opportunities. OpenCourser itself is a testament to this, helping learners navigate the vast offerings of online courses and books.
Successfully navigating self-directed study in a complex area like Monte Carlo simulations involves identifying prerequisites, mastering fundamental programming skills, exploring available tools, and applying knowledge through practical projects. The OpenCourser Learner's Guide can provide valuable strategies for structuring your learning and staying motivated.
Essential Mathematical Prerequisites
Even in a self-directed learning path for Monte Carlo simulations, a foundational understanding of certain mathematical concepts is indispensable. Attempting to learn simulation techniques without this grounding can lead to superficial understanding and difficulty in troubleshooting or adapting methods to new problems. Key areas to focus on include basic probability theory, covering concepts like random variables, probability distributions (common ones like normal, uniform, Poisson, exponential), expected value, and variance.
An understanding of introductory statistics is also crucial, including concepts like sampling, estimation, and hypothesis testing. While advanced calculus and linear algebra are beneficial for deeper theoretical understanding, a conceptual grasp of what derivatives and integrals represent, and how matrices can represent systems of equations, will be helpful. Many online courses designed for a broader audience will review the necessary mathematical concepts as they are introduced, but having some prior familiarity will make the learning process smoother.
Numerous online platforms offer courses in these prerequisite areas, often at introductory university levels. Focusing on grasping the intuition behind the concepts, rather than just memorizing formulas, will be most beneficial for applying them to simulation contexts. For example, understanding why a particular probability distribution is chosen to model a certain type of uncertainty is more important than just knowing the formula for that distribution.
This course provides a good introduction to probability within a data science context.
And these books can serve as excellent resources for self-study in probability and statistical methods.
Programming Language Fundamentals (Python/R)
Practical application of Monte Carlo simulations almost invariably requires programming. Two of the most popular and well-suited languages for this purpose, especially for those starting out or working in data science and quantitative analysis, are Python and R. Both languages boast extensive libraries for numerical computation, statistical analysis, random number generation, and data visualization, which are all essential for implementing Monte Carlo simulations.
For Python, libraries such as NumPy (for numerical operations, especially with arrays), SciPy (for scientific and technical computing, including statistical functions and optimization), Pandas (for data manipulation and analysis), and Matplotlib or Seaborn (for plotting) are fundamental. R, being a language specifically designed for statistical computing and graphics, has many built-in functions and packages (like `dplyr` for data manipulation and `ggplot2` for visualization) that are highly conducive to simulation work.
Learners should focus on mastering the basics of their chosen language: data types, control structures (loops, conditionals), functions, and how to use relevant libraries for generating random numbers from various distributions, performing calculations, and visualizing results. Many online courses offer introductions to Python or R specifically geared towards data analysis or scientific computing, which would be highly relevant. The ability to write clear, efficient, and well-documented code is a valuable skill in itself. Starting with simple simulation problems and gradually increasing complexity is a good learning strategy.
These courses can help you get started with programming for finance and data science, which often involves simulation.
For those interested in lower-level programming, which can be important for performance-critical simulations, C is also a relevant language.
Open-Source Simulation Frameworks
While it's beneficial to learn how to build Monte Carlo simulations from scratch using fundamental programming libraries to understand the underlying mechanics, several open-source frameworks and specialized libraries can simplify and accelerate the development of more complex simulations. These tools often provide pre-built functionalities for common tasks in simulation modeling.
In the Python ecosystem, apart from the core scientific libraries like NumPy and SciPy, you might find packages specifically designed for simulation or probabilistic programming. For instance, `SimPy` is a process-based discrete-event simulation framework. Libraries like `PyMC3` or `Stan` (which has interfaces for Python, R, and other languages) are powerful tools for Bayesian statistics and Markov Chain Monte Carlo (MCMC) methods, which are a sophisticated class of Monte Carlo algorithms. These are particularly useful for fitting complex statistical models and quantifying uncertainty in model parameters.
In R, the `tidyverse` collection of packages provides a comprehensive environment for data manipulation and visualization, which is essential for preparing inputs and analyzing outputs of simulations. R also has numerous packages for specific types of simulations, such_as `simmer` for discrete-event simulation, or various packages for MCMC. Exploring these tools can provide insights into best practices and allow you to tackle more advanced problems without reinventing the wheel. Many of these frameworks have active communities and good documentation, which are valuable resources for self-learners.
Understanding how to work with data in spreadsheets is also a valuable complementary skill, as they are often used for simpler models or for preparing/analyzing data for more complex simulations.
Capstone Project Ideas
One of the most effective ways to solidify understanding and build a portfolio when learning Monte Carlo simulations through self-directed study is to undertake capstone projects. These projects allow you to apply the concepts and tools you've learned to a problem of interest, from start to finish. This practical experience is invaluable for reinforcing knowledge and demonstrating capabilities.
Some project ideas could include:
- Financial Portfolio Simulation: Model the potential returns of a simple investment portfolio consisting of a few assets (e.g., stocks, bonds). Define probability distributions for their expected returns and volatilities (and perhaps correlations). Simulate the portfolio's value over a specific period and calculate metrics like average return, standard deviation of returns, and the probability of achieving a certain financial goal or falling below a certain threshold.
- Project Management Simulation: Model a small project with several tasks, where each task has an uncertain duration. Simulate the project completion time many times to estimate the average completion time and the probability of finishing by a specific deadline. You could extend this to include uncertain costs.
- Simple Game Simulation: Analyze the probabilities of outcomes in a simple game of chance (e.g., a dice game, a simplified card game). For instance, simulate rolling two dice thousands of times to verify the probabilities of different sums.
- Inventory Management: Model a simple inventory system for a product with uncertain demand and lead times for replenishment. Simulate the system over time to estimate average inventory levels, stockout probabilities, and total costs.
- Queuing System: Simulate a simple queuing system (e.g., customers arriving at a single server). Model uncertain arrival rates and service times to estimate average waiting times and queue lengths.
When undertaking such a project, it's important to clearly define the problem, identify the uncertain variables, choose appropriate probability distributions, implement the simulation, analyze the results (including visualizations), and document your process and findings. Starting with a simpler version of a problem and gradually adding complexity is often a good approach.
This course introduces key analytics techniques, some of which can be enhanced or explored further with simulation projects.
These books offer a wealth of methods and examples that can inspire project ideas.
Career Progression with Monte Carlo Expertise
Expertise in Monte Carlo simulations can open doors to a variety of career paths across diverse industries. As organizations increasingly rely on data-driven decision-making and sophisticated risk management, professionals who can develop, implement, and interpret these complex models are in demand. The career trajectory can range from entry-level analytical roles to specialized research positions and leadership opportunities.
The ability to quantify uncertainty and provide probabilistic insights is a valuable skill set. For those considering this path, it's encouraging to know that the skills are often transferable, allowing for flexibility and growth. However, it's also important to have realistic expectations; advanced roles often require significant experience and, in some cases, further education.
If you're new to this field or considering a career pivot, remember that building expertise takes time and continuous learning. Focus on strengthening your foundational knowledge, gaining practical experience, and staying updated with evolving techniques and applications. OpenCourser provides resources like the Career Development section to help you explore various paths.
Entry-Level Roles Requiring Simulation Skills
For individuals starting their careers with a foundational knowledge of Monte Carlo simulations, several entry-level roles can provide valuable experience. These positions often involve supporting more senior analysts or scientists in developing and running models, analyzing data, and preparing reports. A bachelor's or master's degree in a quantitative field like statistics, mathematics, economics, finance, engineering, or computer science is typically expected.
Common entry-level titles might include: Junior Analyst (in finance, business, or operations), Data Analyst, Research Assistant, or Quantitative Analyst Trainee. In these roles, you might be tasked with gathering and cleaning data for simulation inputs, implementing simpler simulation models under supervision, running existing simulation tools, performing sensitivity analyses, and visualizing results. Proficiency in programming languages like Python or R, and familiarity with spreadsheet software, are often required.
These roles provide an excellent opportunity to learn from experienced practitioners, understand how simulations are applied in real-world contexts, and further develop technical and analytical skills. Employers will look for a strong quantitative aptitude, problem-solving abilities, attention to detail, and good communication skills to explain complex results clearly.
Consider exploring these related career paths:
Mid-Career Specialization Paths
As professionals gain experience with Monte Carlo simulations and develop a deeper understanding of their application within a specific industry, various mid-career specialization paths can emerge. These roles often require a master's degree or significant practical experience, and involve greater responsibility in designing, developing, and validating complex simulation models, as well as interpreting and communicating their results to stakeholders.
Specializations might include: Risk Analyst/Manager, focusing on quantifying and managing financial, operational, or project risks using simulation techniques. Quantitative Analyst (Quant), particularly in finance, developing sophisticated models for trading, investment strategies, or derivative pricing. Operations Research Analyst, optimizing complex systems in logistics, manufacturing, or service industries. Data Scientist, where simulation can be a tool for tasks like A/B testing at scale, generating synthetic data, or understanding model uncertainty. Modeling and Simulation Engineer, in fields like aerospace, automotive, or defense, developing simulations of physical systems.
At this stage, individuals are expected to have strong technical skills, a deep understanding of the relevant domain, and the ability to lead projects or mentor junior analysts. Continuous learning is crucial, as new techniques and computational tools are constantly evolving. Pursuing relevant professional certifications or further education can also enhance career progression.
These careers often involve significant use of simulation and modeling techniques.
Leadership Positions in Modeling Teams
With extensive experience and a proven track record in developing and applying Monte Carlo simulations, professionals can advance to leadership positions within modeling and analytics teams. These roles typically require a deep understanding of both the technical aspects of simulation and the business or research context in which they are applied, often coupled with an advanced degree (PhD or specialized Master's) and significant years of experience.
Leadership roles might include: Head of Quantitative Analytics, Director of Risk Management, Manager of Modeling and Simulation, or Principal Data Scientist. Responsibilities often involve setting the strategic direction for the modeling team, overseeing the development and validation of complex models, ensuring best practices are followed, communicating highly technical results to executive leadership, and mentoring and developing team members. They may also be involved in research and development of new modeling methodologies.
Strong leadership, communication, and project management skills are paramount in these positions, in addition to deep technical expertise. The ability to translate complex model outputs into actionable business insights and to navigate the ethical considerations of modeling is also critical. These leaders play a key role in how organizations leverage quantitative methods to make strategic decisions and manage uncertainty.
Cross-Industry Transferable Skills
A significant advantage of developing expertise in Monte Carlo simulations is the high degree of transferability of these skills across different industries. The fundamental principles of modeling uncertainty, random sampling, statistical analysis, and computational implementation are applicable in a wide range of contexts. This provides professionals with considerable career flexibility and the ability to pivot between sectors.
For example, the skills used to model financial risk can be adapted to assess risks in supply chains, energy markets, or environmental projects. Experience in simulating physical systems in engineering can be valuable in developing models for biological systems or even complex social phenomena. The core competencies – quantitative reasoning, problem-solving, programming (often in Python or R), data analysis, and the ability to interpret and communicate probabilistic results – are in demand across finance, technology, healthcare, consulting, government, and research.
This transferability means that investments in learning Monte Carlo methods can have long-term career benefits, even if one's initial industry focus changes. It's a versatile toolkit for anyone who needs to make decisions or predictions in the face of uncertainty. Highlighting these core transferable skills on a resume and during interviews can be beneficial when exploring opportunities in new fields.
Understanding broader analytical topics can enhance skill transferability.
Challenges and Limitations
While Monte Carlo simulations are powerful and versatile tools, they are not without their challenges and limitations. It's crucial for practitioners and decision-makers to be aware of these to use the method effectively and interpret its results appropriately. Acknowledging these aspects helps in setting realistic expectations and ensuring that simulations are applied in a robust and responsible manner.
From computational demands to the inherent difficulties in modeling complex realities, understanding these hurdles is key to successful application. For those new to the field, recognizing these challenges early can guide their learning and help them develop a more nuanced understanding of when and how to best employ Monte Carlo techniques.
Computational Resource Requirements
One of the significant practical challenges of Monte Carlo simulations can be their computational resource requirements. Because accuracy often improves with the number of simulation runs (typically scaling with 1/√N, where N is the number of samples), achieving high precision for complex models can necessitate millions or even billions of iterations. Each iteration might itself involve numerous calculations, especially if the underlying model is intricate or involves many variables.
This can lead to long run times, requiring substantial computing power (CPUs, GPUs) and memory. For very large-scale simulations, access to high-performance computing clusters or cloud computing resources might be necessary. While variance reduction techniques can help to mitigate this by achieving a desired accuracy with fewer samples, they don't eliminate the issue entirely, and implementing them can add complexity.
The "curse of dimensionality" can also be a factor, where the number of samples needed to adequately explore the input space grows exponentially with the number of uncertain input variables. Researchers and practitioners must often make a trade-off between the desired level of accuracy/detail in the model and the available computational budget and time constraints. This is a key consideration in the design of any Monte Carlo study.
Model Validation Difficulties
Model validation – ensuring that the simulation model accurately represents the real-world system or process it is intended to mimic – is a critical and often difficult aspect of Monte Carlo simulations. The adage "garbage in, garbage out" strongly applies; if the underlying model assumptions, input probability distributions, or the relationships between variables are incorrect or poorly specified, the simulation results, no matter how many iterations are run, will be misleading.
Validating a Monte Carlo model can be challenging because the real-world systems being modeled are often complex, and historical data for comparison might be limited, noisy, or not fully representative of future conditions. It's often difficult to know with certainty if the chosen probability distributions for input variables truly reflect their inherent uncertainty. Sensitivity analysis can help identify which assumptions have the most impact on the results, guiding where validation efforts should be focused.
Techniques for validation include comparing simulation outputs to historical data (if available and relevant), checking for logical consistency in the results, having domain experts review the model's structure and assumptions, and performing "extreme condition" tests to see if the model behaves plausibly under highly unlikely scenarios. However, complete validation is often elusive, especially for models of novel systems or those predicting far into the future. This underscores the importance of clearly documenting all assumptions and acknowledging the potential limitations of the model.
Interpretation of Probabilistic Results
While a key strength of Monte Carlo simulations is their ability to produce probabilistic results, interpreting these results correctly can be a challenge, especially for non-technical stakeholders. Instead of a single, definitive answer, a simulation provides a distribution of possible outcomes and their likelihoods. Communicating this range of possibilities and the associated uncertainties effectively requires care.
For example, a result might be presented as a 90% confidence interval, or the probability of exceeding a certain threshold. It's important to ensure that decision-makers understand what these probabilistic statements mean and, equally importantly, what they don't mean. A common pitfall is to focus solely on the average or most likely outcome, ignoring the potential for extreme events, even if they have a lower probability.
Visualizations like histograms, cumulative distribution functions (CDFs), and scatter plots can be very helpful in conveying the full picture of the results. However, there's also the risk of misinterpretation if these are not clearly explained. Analysts must be skilled in translating the statistical outputs into meaningful insights that can inform decision-making, highlighting not just the expected outcome but also the range of uncertainty and key risk factors.
These courses touch on analytics and data presentation, which are relevant for communicating simulation results.
Common Implementation Pitfalls
Implementing Monte Carlo simulations involves several potential pitfalls that can lead to inaccurate or misleading results. Awareness of these common issues is crucial for both developers and users of simulation models.
One common pitfall is the incorrect specification of input probability distributions. Choosing a distribution that doesn't accurately reflect the uncertainty of an input variable can significantly bias the results. Similarly, failing to correctly model correlations between input variables can lead to an underestimation or overestimation of overall risk. For instance, if two risk factors tend to move together but are modeled as independent, the simulation might not capture the true combined impact.
Errors in the underlying model logic or mathematical formulas are another frequent issue. Even small coding errors can propagate and lead to large inaccuracies in the final output. Thorough debugging and testing are essential. [ime64r]
Insufficient number of simulation runs can lead to results that haven't converged and are therefore unreliable. It's important to assess convergence and ensure that the number of iterations is adequate for the desired level of precision. Conversely, running far too many iterations without a clear benefit in accuracy can lead to wasted computational resources.
Finally, overconfidence in the model's predictions without fully acknowledging its assumptions and limitations is a significant pitfall. All models are simplifications of reality, and it's vital to communicate the uncertainty inherent in the simulation results themselves.
Emerging Trends in Monte Carlo Methods
The field of Monte Carlo simulations is not static; it continues to evolve with advances in computing technology, mathematical theory, and integration with other cutting-edge disciplines. Several emerging trends are shaping the future of how these powerful methods are developed and applied, promising even greater capabilities in tackling complex problems and extracting insights from data.
These trends reflect a move towards more sophisticated, efficient, and widely applicable simulation techniques. For researchers and practitioners, staying abreast of these developments is key to leveraging the full potential of Monte Carlo methods in their respective domains.
Machine Learning Integration
A significant and rapidly growing trend is the integration of Monte Carlo methods with machine learning (ML). This synergy works in both directions. ML techniques can be used to enhance Monte Carlo simulations, for instance, by building surrogate models (also known as emulators or meta-models) that can approximate the output of a computationally expensive simulation model much more quickly. This allows for faster exploration of the parameter space. ML can also help in learning complex input probability distributions from data or in developing more effective variance reduction techniques.
Conversely, Monte Carlo methods are fundamental to many ML algorithms and practices. For example, resampling techniques like bootstrapping, used for estimating model accuracy and uncertainty, are based on Monte Carlo sampling. In Bayesian machine learning, Markov Chain Monte Carlo (MCMC) methods are crucial for approximating posterior distributions of model parameters. Reinforcement learning algorithms often use Monte Carlo methods to estimate value functions or simulate future trajectories.
This deep interplay allows for the development of more powerful and robust analytical tools. For example, combining the predictive power of ML with the scenario analysis strength of Monte Carlo simulations can lead to improved forecasting and risk assessment in dynamic environments like financial markets. As both fields continue to advance, their integration is expected to unlock new capabilities.
For those interested in this intersection, exploring these topics is a good start.
This book provides insights into a related advanced ML topic.
Quantum Computing Applications
While still in its relatively early stages, quantum computing holds the potential to revolutionize certain types of Monte Carlo simulations. Classical Monte Carlo methods, especially for high-dimensional problems or those requiring extreme precision, can be computationally prohibitive due to the sheer number of samples needed. Quantum algorithms, by leveraging principles like superposition and entanglement, offer the possibility of significant speedups for specific computational tasks.
One area where quantum computing could impact Monte Carlo methods is in "quantum Monte Carlo" (QMC) algorithms. Some QMC algorithms aim to achieve a quadratic speedup in the number of samples needed to reach a certain level of accuracy for estimating expectation values (e.g., in financial modeling or numerical integration). This means that if a classical Monte Carlo simulation needs N samples, a quantum version might achieve similar accuracy with only √N samples. This could make previously intractable simulation problems feasible.
However, realizing these theoretical advantages in practice faces significant hurdles, including the development of fault-tolerant quantum computers with a sufficient number of qubits, as well as designing efficient quantum algorithms for specific Monte Carlo tasks. Research is ongoing in areas like quantum algorithms for option pricing, risk analysis, and solving differential equations that underpin many simulation models. While widespread practical application is likely still some years away, the long-term potential is considerable.
This book explores Quantum Monte Carlo methods in more detail.
Real-Time Simulation Advancements
The demand for real-time or near real-time Monte Carlo simulations is growing in various applications where decisions need to be made quickly based on rapidly changing data. Examples include algorithmic trading in finance, dynamic resource allocation in logistics, real-time risk assessment in autonomous systems, or interactive decision support tools. Traditionally, the computational intensity of Monte Carlo methods made them more suited for offline analysis.
Advancements in several areas are making real-time simulations more feasible. These include the continued growth in raw computing power (CPUs, GPUs), the development of more efficient algorithms (including improved variance reduction techniques and specialized MCMC samplers), and the use of parallel and distributed computing architectures. Cloud computing platforms also offer scalable resources that can be dynamically allocated for intensive simulation tasks.
Furthermore, the integration with machine learning, particularly the use of surrogate models, can play a crucial role. A complex Monte Carlo model can be run offline to train a faster surrogate model, which can then be used for real-time predictions or decision-making, with periodic retraining of the surrogate as new data becomes available or the underlying system changes. While achieving true real-time performance for highly complex simulations remains a challenge, the trend is towards increasingly responsive and dynamic simulation capabilities.
Open-Source Community Developments
The vibrant and collaborative nature of the open-source community continues to be a major driver of innovation and accessibility in Monte Carlo methods and computational science in general. A vast ecosystem of open-source software tools, libraries, and frameworks significantly lowers the barrier to entry for learning and applying these techniques. Languages like Python and R, which are themselves open-source, form the backbone of much of this development.
Communities around specific libraries (e.g., NumPy, SciPy, PyMC3, Stan, and the R package ecosystem) actively contribute to their development, documentation, and user support. This collaborative effort leads to continuous improvement of existing tools, the creation of new functionalities, and the sharing of best practices. Online platforms like GitHub host countless open-source projects related to simulation, allowing for code sharing, peer review, and collaborative problem-solving.
For learners and practitioners, this open-source landscape provides invaluable resources. It means access to powerful tools without expensive licensing fees, extensive documentation, tutorials, and a community to turn to for help. It also fosters transparency and reproducibility in research and analysis, as code and methods can be openly shared and scrutinized. The ongoing contributions from this global community are crucial for democratizing access to advanced computational methods like Monte Carlo simulations and for pushing the boundaries of what's possible.
Ethical Considerations in Simulation Modeling
The power of Monte Carlo simulations and other advanced modeling techniques also comes with significant ethical responsibilities. When these models are used to inform decisions that can have substantial impacts on individuals, organizations, or society as a whole – such as in financial lending, resource allocation, public policy, or medical diagnostics – it's crucial to consider the ethical implications of their design, implementation, and interpretation.
Ignoring these considerations can lead to unfair outcomes, perpetuate biases, or result in a false sense of certainty that masks underlying risks. A responsible approach to simulation modeling requires a commitment to transparency, fairness, and a critical awareness of the model's limitations and potential societal consequences.
Model Bias and Input Assumptions
A critical ethical consideration in Monte Carlo simulations is the potential for model bias stemming from the input assumptions and the way the model is structured. All models are simplifications of reality, and the choices made by the modeler about which variables to include, how to represent their uncertainty with probability distributions, and how to define the relationships between them can inadvertently introduce or amplify biases.
For example, if historical data used to inform input distributions reflects past discriminatory practices (e.g., in lending or hiring), a simulation based on this data may perpetuate those biases in its predictions, leading to unfair outcomes for certain groups. If the modeler's own unconscious biases influence the selection of variables or the framing of the problem, this can also skew the results. It's also crucial to recognize that assumptions about the future based on past data might not hold, especially in rapidly changing environments or when dealing with unprecedented events.
Ethical practice requires a diligent effort to identify and mitigate potential sources of bias in input data and model assumptions. This involves critically examining data sources, questioning the appropriateness of chosen probability distributions, and considering whether the model adequately represents the diversity of the population or system being studied. Transparency about these assumptions and potential biases is paramount.
Transparency in Probabilistic Outcomes
Monte Carlo simulations produce probabilistic outcomes, providing a range of possibilities and their likelihoods rather than a single definitive answer. Ethical use of these simulations demands transparency in how these probabilistic outcomes are communicated and interpreted, especially when they inform decisions affecting individuals or the public.
It can be tempting for decision-makers to focus on the most favorable or most likely outcome, while downplaying or ignoring less probable but potentially severe negative outcomes. Ethical communication requires presenting the full spectrum of results, including the uncertainties and the probabilities of adverse events, in a way that is understandable to the relevant stakeholders, even if they are not technical experts. This includes clearly explaining the assumptions underlying the simulation and the limitations of the model.
Lack of transparency can lead to misplaced confidence in the model's predictions or to decisions that do not adequately account for risk. For instance, if a financial product's potential returns are advertised based on the average outcome of a simulation, without clearly disclosing the probability of significant losses, this could be misleading to investors. Ensuring that probabilistic information is conveyed honestly and comprehensively is a key ethical responsibility.
Regulatory Compliance Aspects
In many domains, particularly finance, healthcare, and environmental management, the use of simulation models, including Monte Carlo methods, is subject to regulatory oversight and compliance requirements. Regulators may mandate specific modeling standards, validation procedures, or transparency and disclosure rules to ensure that models are sound, used appropriately, and do not pose undue risks to consumers, the financial system, or public safety.
For example, financial institutions using internal models (which may involve Monte Carlo simulations) to calculate regulatory capital must demonstrate to supervisors that their models are conceptually sound, empirically validated, and used consistently. In drug development, simulations used to predict efficacy or dosage may need to meet standards set by health authorities. Environmental impact assessments often rely on simulations, and these must typically adhere to established guidelines and undergo review.
Ethical practice in these contexts involves a commitment to meeting or exceeding these regulatory standards. This includes rigorous model validation, thorough documentation of methodologies and assumptions, and transparent reporting of results to regulatory bodies. Failure to comply can have serious legal and reputational consequences, and more importantly, can undermine the public trust in the systems that rely on these models.
Case Studies of Misuse
Examining case studies where simulation models, including those with Monte Carlo components, have been misused or have led to unintended negative consequences can provide valuable lessons in ethical practice. While specific, publicly detailed cases of purely Monte Carlo misuse can be hard to pinpoint without proprietary information, broader examples from financial modeling and risk management offer insights.
For instance, the financial crisis of 2008 highlighted how over-reliance on complex financial models (some of which used simulation techniques for pricing and risk assessment of mortgage-backed securities) with flawed assumptions or insufficient understanding of their limitations contributed to systemic risk. Models might have underestimated the probability of extreme events or failed to capture critical correlations between different asset classes during a crisis.
In other areas, a model might be used to justify a predetermined decision, with input assumptions manipulated to produce the desired outcome. Or, a lack of transparency about a model's uncertainty could lead to policies that are not robust to real-world variability. These examples underscore the importance of critical evaluation of model assumptions, rigorous validation, transparency about limitations, and an awareness that models are tools to aid judgment, not replace it. Learning from past mistakes is crucial for fostering a more ethical and responsible approach to simulation modeling.
Frequently Asked Questions (Career Focus)
For those considering a career that involves Monte Carlo simulations, or looking to incorporate these skills into their current profession, several practical questions often arise. Addressing these can help clarify the path forward and set realistic expectations. Remember, building a career in any specialized quantitative field is a journey that combines education, practical experience, and continuous learning. If you're exploring options, OpenCourser's browsing features can help you discover relevant courses and topics to build your expertise.
What industries hire Monte Carlo specialists most frequently?
Monte Carlo specialists are sought after in a variety of industries that deal with uncertainty, risk, and complex system modeling. The financial services industry is a major employer, with roles in investment banking, asset management, insurance, and risk management. Here, specialists use simulations for portfolio optimization, option pricing, credit risk modeling, and regulatory capital calculations.
The engineering sector (including aerospace, automotive, civil, and manufacturing) also frequently hires individuals with simulation skills for tasks like reliability analysis, design optimization, project risk management, and process simulation. Consulting firms, both management and technical, often employ Monte Carlo experts to help clients across various industries solve complex problems involving forecasting and decision-making under uncertainty.
Other notable industries include energy and utilities (for modeling energy markets, resource extraction, or grid reliability), pharmaceuticals and healthcare (for drug development, clinical trial simulation, and epidemiological modeling), technology companies (especially in areas like data science, AI research, and logistics/supply chain optimization), and government and defense (for policy analysis, defense simulations, and operations research). The breadth of applications means opportunities can be found in many sectors that value quantitative analysis and data-driven insights.
How much programming is required for entry-level roles?
For most entry-level roles involving Monte Carlo simulations, a foundational level of programming proficiency is generally required. You typically won't need to be an expert software developer, but you should be comfortable writing, understanding, and debugging code in at least one relevant language, most commonly Python or R. Familiarity with common data science and numerical computing libraries (e.g., NumPy, SciPy, Pandas in Python; dplyr, ggplot2 in R) is also highly beneficial.
Entry-level tasks might involve implementing relatively straightforward simulation models, modifying existing code, running simulations using established tools or scripts, processing and visualizing the output data, and performing basic sensitivity analyses. Therefore, understanding programming concepts like variables, data structures (lists, arrays, data frames), control flow (loops, conditional statements), and functions is essential. Experience with version control systems like Git can also be a plus.
While some roles might involve using specialized simulation software with graphical user interfaces, the trend is towards using programming languages for greater flexibility and customization. Many online courses and resources are available to build these foundational programming skills, often specifically tailored for data analysis or scientific computing contexts. OpenCourser's programming section offers a wide variety of courses to get started.
These courses provide a good starting point for learning programming in relevant languages.
Can I transition from theoretical math to applied simulations?
Yes, transitioning from a background in theoretical mathematics to applied simulations, including Monte Carlo methods, is definitely possible and can be a very rewarding path. A strong foundation in theoretical mathematics provides many ofauspicious the essential building blocks for understanding and developing sophisticated simulation models. Concepts from probability theory, statistics, calculus, and linear algebra are directly applicable.
The key to making this transition successfully often lies in complementing theoretical knowledge with practical, applied skills. This includes gaining proficiency in programming languages commonly used for simulation (like Python or R), learning how to use relevant computational libraries, and understanding how to translate abstract mathematical concepts into concrete computational algorithms. It also involves developing an appreciation for the practical aspects of modeling, such as data handling, model validation, and the interpretation of results in a real-world context.
Taking online courses focused on applied statistics, data science, computational methods, or specific domains like financial modeling can be very helpful. Working on hands-on projects, even personal ones, to build a portfolio of applied work is also crucial. Emphasize your strong analytical and problem-solving skills derived from your math background, while demonstrating a commitment to learning the applied tools and techniques. Many employers value the rigorous thinking that a theoretical math education instills, especially when combined with practical simulation capabilities.
This course bridges theoretical concepts with computational application in data science.
What certifications enhance career prospects?
While specific "Monte Carlo Simulation" certifications are not as common or standardized as, for example, project management or IT certifications, several professional certifications can enhance career prospects for individuals working in fields that heavily utilize simulation. The value of a certification often depends on the specific industry and role.
In finance, certifications like the Chartered Financial Analyst (CFA) or Financial Risk Manager (FRM) are highly respected and cover quantitative methods, including aspects of risk modeling and simulation. [4161ts, mxc3wi] For those in actuarial science, professional actuarial exams (e.g., from the Society of Actuaries or Casualty Actuarial Society) involve rigorous testing in probability, statistics, and risk modeling. [loscgc]
In data science and analytics, while less about simulation specifically, certifications in specific programming languages (like Python), cloud platforms (AWS, Azure, GCP), or machine learning can demonstrate valuable complementary skills. Some universities or online platforms also offer certificates for completing specializations or series of courses in areas like data science, business analytics, or quantitative finance, which may include modules on simulation. [0y9nfl]
Ultimately, while certifications can be a useful credential, employers will typically place more weight on demonstrated skills, practical experience, a strong educational foundation, and the ability to solve real-world problems using simulation techniques. A portfolio of projects or research showcasing your abilities can often be more impactful than certifications alone. However, in certain fields, recognized professional designations can certainly provide a competitive edge.
How does Monte Carlo expertise compare to machine learning skills?
Monte Carlo expertise and machine learning (ML) skills are distinct yet often complementary, and both are highly valued in today's data-driven world. Monte Carlo simulations are primarily about understanding and quantifying uncertainty by modeling systems with random inputs to explore a range of possible outcomes. They are often used when the underlying model or process can be reasonably defined, even if it involves randomness.
Machine learning, on the other hand, is more focused on enabling computers to learn patterns and make predictions from data without being explicitly programmed for each specific task. ML excels at finding complex relationships in large datasets and can be used for tasks like classification, regression, clustering, and generating new data.
The two fields are increasingly intertwined. ML can be used to build components of Monte Carlo models (e.g., learning input distributions from data or creating fast surrogate models). Conversely, Monte Carlo methods are used within ML, for example, in resampling techniques like bootstrapping, or in algorithms like MCMC for Bayesian inference and Monte Carlo Tree Search in reinforcement learning.
In terms of career prospects, both skill sets are in high demand. ML has seen explosive growth and is sought in a vast range of applications. Expertise in Monte Carlo simulations is perhaps more specialized but crucial in fields that heavily rely on probabilistic modeling and risk assessment, like finance, engineering, and certain sciences. Professionals who possess skills in both areas are particularly well-positioned, as they can leverage the strengths of each approach to tackle complex problems in more sophisticated ways. Many data science roles, for instance, benefit from a toolkit that includes both ML and simulation techniques. [jj2ao8]
Consider exploring these related topics for a broader perspective.
What global markets value this skill set?
The skills associated with Monte Carlo simulations are valued in developed and increasingly in emerging global markets, largely mirroring the industries that rely on sophisticated quantitative analysis and risk management. Major financial centers such as New York, London, Tokyo, Hong Kong, Singapore, and Frankfurt have a consistent demand for quantitative professionals, including those with Monte Carlo expertise, in their banking, investment management, and insurance sectors. [mxc3wi, 09wyfb]
Beyond finance, countries with strong technology and engineering sectors, such as the United States (Silicon Valley, Seattle, Boston), Germany, Japan, South Korea, and increasingly China and India, also value these skills for applications in R&D, manufacturing, logistics, and data science. [jj2ao8, epuo6h] The energy sector, with its global footprint, also utilizes simulation for exploration, production, and market analysis, creating opportunities in regions rich in natural resources or with significant renewable energy investments.
Furthermore, international organizations, development banks, and global consulting firms hire individuals with these skills for projects worldwide. The rise of remote work and globalized data science teams also means that opportunities may not be strictly tied to physical location. As more industries globally embrace data-driven decision-making and advanced analytics, the demand for individuals who can model uncertainty and provide probabilistic insights through techniques like Monte Carlo simulations is likely to continue growing across a wide range of geographic markets.
Conclusion
Monte Carlo simulations represent a powerful and versatile approach to understanding and navigating uncertainty in a wide array of fields. From their origins in the mid-20th century to their current sophisticated applications, these methods have become indispensable for anyone needing to make informed decisions in the face of randomness and complexity. Whether you are a student just beginning to explore quantitative methods, a professional looking to enhance your analytical toolkit, or a researcher pushing the boundaries of knowledge, a solid understanding of Monte Carlo simulations can be a significant asset.
The journey to mastering these techniques involves a blend of theoretical understanding, practical programming skills, and domain-specific knowledge. While the path can be challenging, the ability to model complex systems, quantify risk, and explore a spectrum of possible futures offers profound insights and can lead to more robust and effective decision-making. As computational power continues to grow and these methods become further integrated with other advanced technologies like machine learning, the importance and applicability of Monte Carlo simulations are only set to increase. We encourage you to continue your exploration of this fascinating and impactful field, utilizing resources like OpenCourser to find the courses and books that best suit your learning journey.