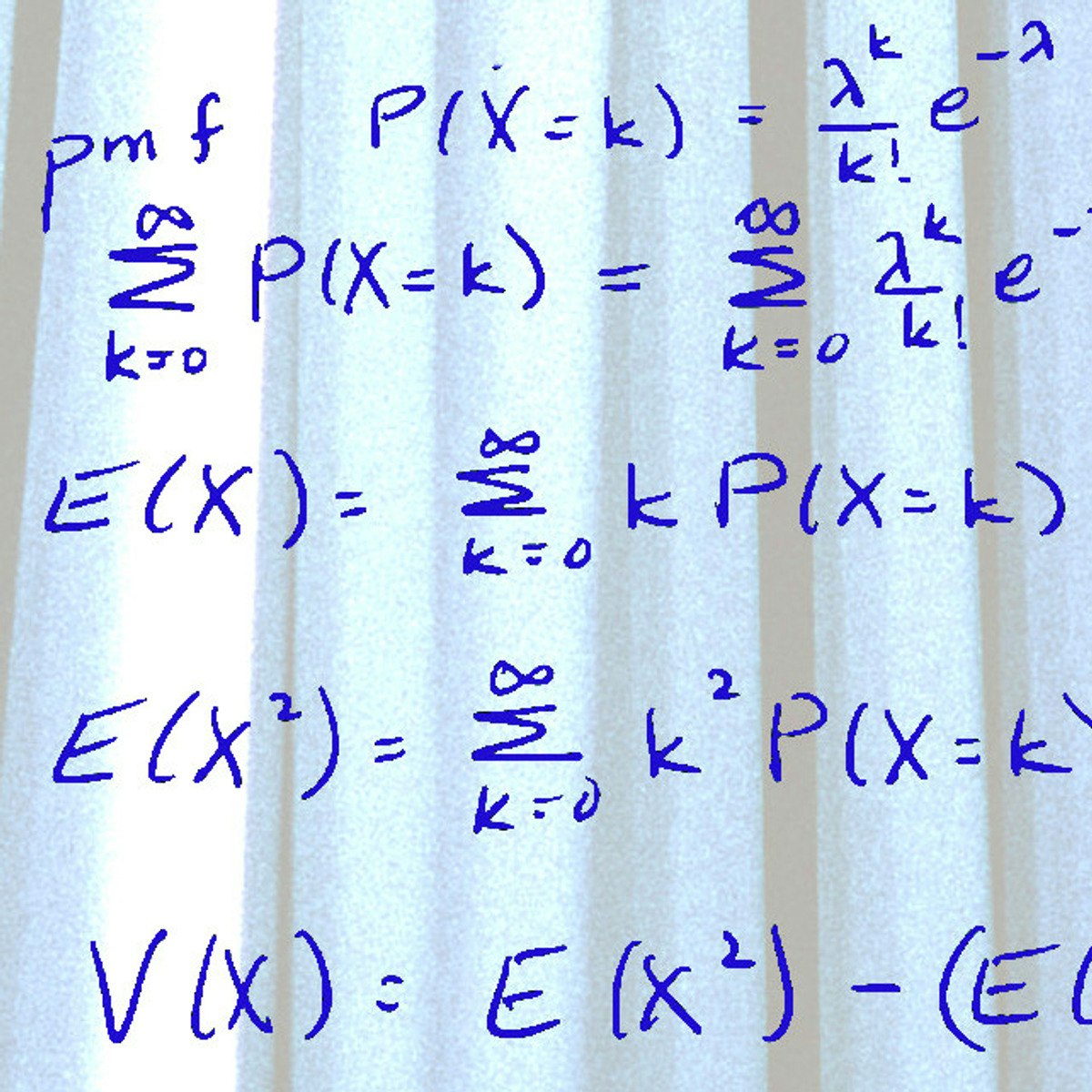Conditional Probability
Navigating Uncertainty: A Comprehensive Guide to Conditional Probability
Conditional probability is a fundamental concept in probability theory that describes the likelihood of an event occurring, given that another event has already happened. It allows us to update our beliefs about an outcome in light of new evidence. At its core, it helps answer the question: "How does the probability of A change if we know B has occurred?" This seemingly simple idea is a cornerstone for reasoning under uncertainty and plays a pivotal role in numerous fields that shape our daily lives.
Understanding conditional probability opens doors to fascinating applications. Imagine the ability to more accurately assess the chances of a patient having a particular condition given certain test results, or to refine weather forecasts based on current atmospheric data. It's also a key ingredient in the algorithms that power search engines, spam filters, and recommendation systems, learning from your interactions to provide more relevant results. The intellectual journey into conditional probability is one of discovering how to quantify and manage uncertainty, a skill increasingly vital in a data-driven world.
Introduction to Conditional Probability
This section will lay the groundwork for understanding conditional probability, starting with its definition and basic formula, illustrating its use with real-world scenarios, and touching upon its relationship with other probabilistic concepts and its historical roots. The aim is to provide an intuitive grasp before diving into more mathematical rigor.
Definition and Basic Formula
Conditional probability is the probability of an event (let's call it A) occurring, given that another event (B) has already occurred. This is typically written as P(A|B), and read as "the probability of A given B." The basic formula to calculate conditional probability is P(A|B) = P(A∩B) / P(B), where P(A∩B) is the probability that both events A and B occur (their intersection), and P(B) is the probability of event B occurring. It's crucial that P(B) is not zero, as we cannot condition on an event that has no chance of happening.
Think of it like narrowing down your focus. Initially, you might be interested in the probability of A happening out of all possible outcomes. But once you know that B has definitely happened, you're only interested in the outcomes where B is true, and within that smaller set, what the chances of A also being true are. This adjustment of probability based on new information is a fundamental aspect of learning from data.
For instance, consider a standard deck of 52 playing cards. The probability of drawing a King is 4/52 (or 1/13). However, if you are told that the card drawn is a face card (Jack, Queen, or King), the conditional probability of drawing a King, given it's a face card, changes. There are 12 face cards, 4 of which are Kings. So, P(King | Face Card) = 4/12 = 1/3. The knowledge that the card is a face card increases the probability of it being a King.
Real-World Examples
Conditional probability is not just an abstract mathematical concept; it's deeply embedded in how we understand and navigate the world. One prominent example is in medical testing. Suppose a patient takes a test for a certain disease. The conditional probability P(Disease | Positive Test) – the probability the patient actually has the disease given a positive test result – is of critical importance. This calculation involves knowing the probability of a positive test if the person has the disease (sensitivity), the probability of a negative test if the person does not have the disease (specificity), and the overall prevalence of the disease in the population.
Weather forecasting is another domain heavily reliant on conditional probability. When a meteorologist says there's an 80% chance of rain tomorrow, this is often a conditional probability. It might be P(Rain | Current weather patterns, historical data showing similar patterns led to rain). They are conditioning on a vast amount of current and past information to predict a future event.
In finance, conditional probability is used in risk assessment. For example, an analyst might want to calculate the probability of a stock's price falling, given that a certain economic indicator (like interest rates) has risen. This helps in making investment decisions by understanding how different events might impact each other.
Relationship to Joint and Marginal Probability
To fully appreciate conditional probability, it's helpful to understand its connection to joint and marginal probabilities. Marginal probability is the probability of a single event occurring, irrespective of other events. For example, P(A) is the marginal probability of event A. In our card example, P(King) = 4/52 is a marginal probability.
Joint probability, on the other hand, is the probability of two or more events occurring simultaneously. This is denoted as P(A∩B) or P(A, B). For instance, the probability of drawing a card that is both a King and a Spade is P(King ∩ Spade) = 1/52. The formula for conditional probability, P(A|B) = P(A∩B) / P(B), directly shows this relationship: conditional probability is the ratio of the joint probability of both events occurring to the marginal probability of the condition event occurring.
Rearranging the formula, we also get P(A∩B) = P(A|B) * P(B), which is known as the multiplication rule. This rule states that the probability of both A and B happening is the probability of B happening multiplied by the probability of A happening given that B has already happened. These relationships are fundamental building blocks for more complex probabilistic models.
Historical Context
The roots of conditional probability are deeply intertwined with the development of probability theory itself, with significant contributions emerging in the 17th and 18th centuries. While early ideas of probability were often linked to games of chance, the formalization of conditional probability is heavily associated with the work of Thomas Bayes, an 18th-century English statistician and philosopher.
Bayes' Theorem, which provides a way to update the probability of a hypothesis based on new evidence, is a direct application and extension of conditional probability concepts. His work, posthumously published as "An Essay towards solving a Problem in the Doctrine of Chances" (1763), laid a crucial foundation for what is now known as Bayesian statistics. This approach to statistics, which heavily relies on conditional probabilities to update beliefs, has become increasingly influential in various fields, especially with the rise of computational power that allows for complex Bayesian models to be implemented.
Before Bayes, mathematicians like Abraham de Moivre also worked on problems involving dependent events, contributing to the evolving understanding of how the occurrence of one event could influence the probability of another. The development of these ideas was driven by a desire to reason more systematically about uncertainty in various domains, from gambling to annuities and scientific observation.
Mathematical Foundations
For those seeking a more rigorous understanding, particularly university students and academic researchers, delving into the mathematical underpinnings of conditional probability is essential. This section explores key theorems, concepts, and tools that form the backbone of advanced probabilistic reasoning and its applications in research and complex problem-solving.
These foundational courses can provide a solid understanding of probability theory, including conditional probability and its mathematical derivations. They often cover the necessary calculus and set theory prerequisites.
The following books are standard texts that delve deeply into the mathematical foundations of probability, including thorough treatments of conditional probability, Bayes' theorem, and related concepts.
Bayes' Theorem Derivation and Applications
Bayes' Theorem is a cornerstone of probability theory and a direct consequence of the definition of conditional probability. It describes how to update the probability of a hypothesis based on new evidence. The theorem is stated as: P(A|B) = [P(B|A) * P(A)] / P(B).
Let's break down its derivation. We know from the definition of conditional probability that: 1. P(A|B) = P(A∩B) / P(B) 2. P(B|A) = P(B∩A) / P(A) Since P(A∩B) is the same as P(B∩A) (the probability of both A and B occurring is the same regardless of order), we can write: P(A∩B) = P(A|B) * P(B) P(B∩A) = P(B|A) * P(A) Therefore, P(A|B) * P(B) = P(B|A) * P(A). Dividing by P(B) (assuming P(B) ≠ 0), we arrive at Bayes' Theorem: P(A|B) = [P(B|A) * P(A)] / P(B).
In this formula:
- P(A|B) is the posterior probability: the probability of hypothesis A being true after observing evidence B.
- P(B|A) is the likelihood: the probability of observing evidence B if hypothesis A is true.
- P(A) is the prior probability: the initial probability of hypothesis A being true before observing evidence B.
- P(B) is the marginal likelihood or evidence: the total probability of observing evidence B. This can be expanded using the law of total probability (discussed later).
Applications of Bayes' Theorem are widespread, including medical diagnosis (updating the probability of a disease given test results), spam filtering (updating the probability that an email is spam given the words it contains), machine learning (in Naive Bayes classifiers), and even in legal reasoning (updating the probability of guilt given new evidence). It provides a formal framework for learning from experience.
These courses specifically touch upon Bayesian thinking and its applications, which are direct extensions of conditional probability.
For those interested in a deeper dive into Bayesian methods, these books are highly recommended.
Conditional Independence Concepts
Conditional independence is a crucial concept when dealing with multiple events. Two events A and B are said to be conditionally independent given a third event C if the occurrence or non-occurrence of A does not affect the probability of B occurring, once C is known to have occurred, and vice-versa. Mathematically, A and B are conditionally independent given C if P(A|B∩C) = P(A|C), provided P(B∩C) > 0. An equivalent statement is P(A∩B|C) = P(A|C)P(B|C).
It is important to distinguish conditional independence from marginal independence. Two events can be marginally dependent but conditionally independent, or marginally independent but conditionally dependent. For example, consider a scenario where a student's score on a difficult exam (A) and their need for extra tutoring (B) might seem dependent. However, if we condition on their prior knowledge of the subject (C), they might become conditionally independent. Knowing they have high prior knowledge (C) might explain both a high score (A) and no need for tutoring (B), making A and B independent given C.
Understanding conditional independence is vital for constructing probabilistic graphical models, such as Bayesian networks. These models use conditional independence relationships to simplify the representation of joint probability distributions over many variables, making complex systems more tractable to analyze. It allows for more efficient inference and learning in these models.
Probability Tree Diagrams
Probability tree diagrams are visual tools that help in calculating probabilities for sequences of events, especially when conditional probabilities are involved. Each branch in the tree represents an event, and the probability of that event is written on the branch. The sum of probabilities emanating from any single node must equal 1.
To use a tree diagram for conditional probabilities, you start with the initial events and their marginal probabilities. Subsequent branches represent conditional events, with their probabilities being conditional on the events in the preceding branches. To find the probability of a sequence of events (a path through the tree), you multiply the probabilities along the branches of that path. This is a direct application of the multiplication rule derived from conditional probability: P(A∩B) = P(B) * P(A|B).
For example, imagine drawing two balls from an urn containing 3 red balls and 2 blue balls without replacement. The first draw:
- P(Red1) = 3/5
- P(Blue1) = 2/5
The second draw (conditional on the first):
- If Red1 was drawn: P(Red2|Red1) = 2/4, P(Blue2|Red1) = 2/4
- If Blue1 was drawn: P(Red2|Blue1) = 3/4, P(Blue2|Blue1) = 1/4
A tree diagram would clearly show these paths and probabilities. To find the probability of drawing two red balls, P(Red1 ∩ Red2), you would multiply P(Red1) * P(Red2|Red1) = (3/5) * (2/4) = 6/20 = 3/10. Tree diagrams are particularly useful for visualizing and solving problems involving sequential decisions or outcomes. Many introductory probability courses utilize these diagrams to build intuition.
Law of Total Probability
The law of total probability is a fundamental rule relating marginal probabilities to conditional probabilities. It states that if you have a set of mutually exclusive and exhaustive events B1, B2, ..., Bn (meaning one and only one of these events must occur), then the probability of another event A can be expressed as: P(A) = Σ P(A|Bi) * P(Bi) for all i from 1 to n.
In simpler terms, the probability of event A is a weighted average of its conditional probabilities P(A|Bi), where the weights are the probabilities of the conditioning events P(Bi). This law is extremely useful when it's easier to calculate or reason about the probability of A under different conditions (the Bi's) than it is to calculate P(A) directly.
For instance, suppose a factory produces items using three different machines (M1, M2, M3), which account for 50%, 30%, and 20% of production, respectively (these are P(M1), P(M2), P(M3)). Each machine has a different defect rate: P(Defect|M1) = 0.01, P(Defect|M2) = 0.02, P(Defect|M3) = 0.03. To find the overall probability of a randomly selected item being defective, P(Defect), we use the law of total probability: P(Defect) = P(Defect|M1)P(M1) + P(Defect|M2)P(M2) + P(Defect|M3)P(M3) P(Defect) = (0.01 * 0.50) + (0.02 * 0.30) + (0.03 * 0.20) = 0.005 + 0.006 + 0.006 = 0.017. The law of total probability is also crucial in the denominator of Bayes' Theorem, where P(B) is often calculated by summing over all possible hypotheses Ai: P(B) = Σ P(B|Ai)P(Ai).
Conditional Probability in Industry Applications
Conditional probability is not confined to academic exercises; it is a powerful tool with tangible applications across a multitude of industries. Professionals, from financial analysts to machine learning engineers, leverage its principles to make informed decisions, build predictive models, and optimize processes. This section will highlight some key areas where conditional probability drives significant value and return on investment (ROI).
Understanding conditional probability is often a prerequisite or a core component in these applied fields. These courses offer insights into how probability and statistics are used in business and machine learning contexts.
These books explore applications of probabilistic and statistical modeling, including machine learning, which heavily relies on conditional probability.
Risk Assessment Models in Finance
In the financial sector, managing risk is paramount. Conditional probability plays a vital role in building sophisticated risk assessment models. For example, credit scoring models estimate the probability of a borrower defaulting on a loan, given various factors such as their credit history, income, and employment status. P(Default | Applicant's Profile) helps lenders make decisions about loan approvals and interest rates.
Market risk models use conditional probabilities to assess the likelihood of significant losses in investment portfolios given certain market movements (e.g., P(Portfolio Loss > X% | Market Index Drops Y%)). Value at Risk (VaR) and Conditional Value at Risk (CVaR) are common metrics that rely on these probabilistic assessments. Furthermore, in fraud detection, systems analyze transactions and calculate the probability of a transaction being fraudulent given its characteristics and comparison to historical patterns, P(Fraud | Transaction Features). This allows financial institutions to flag and investigate suspicious activities, minimizing losses and protecting customers. The ability to quantify and predict risk based on evolving conditions is a key competitive advantage.
To explore further, you might consider browsing courses in Finance & Economics on OpenCourser for more context on financial modeling and risk management.
Machine Learning Algorithms (Naive Bayes Classifiers)
Many machine learning algorithms are built upon the principles of conditional probability. One of the most direct examples is the Naive Bayes classifier. This algorithm is used for classification tasks, such as categorizing emails as spam or not spam, or identifying the topic of a news article. It's called "naive" because it makes a strong (often simplistic) assumption that the features (e.g., words in an email) are conditionally independent given the class (e.g., spam or not spam).
The Naive Bayes classifier uses Bayes' Theorem to calculate the probability of a class given a set of features: P(Class | Features) = [P(Features | Class) * P(Class)] / P(Features). Due to the conditional independence assumption, P(Features | Class) can be simplified to the product of P(Feature_i | Class) for each feature. Despite its "naive" assumption, Naive Bayes often performs surprisingly well, especially in text classification and medical diagnosis, and it is computationally efficient. Understanding conditional probability is essential for grasping how such algorithms learn from data and make predictions.
For those interested in the practical application of these algorithms, exploring machine learning courses can provide hands-on experience.
Quality Control Processes in Manufacturing
In manufacturing, maintaining high product quality is crucial for customer satisfaction and cost efficiency. Conditional probability is employed in quality control processes to identify and mitigate defects. For instance, a manufacturer might want to know the probability that a product is defective given that it came from a specific machine or production line: P(Defect | Machine A).
Statistical Process Control (SPC) charts often implicitly use conditional probabilities by monitoring process variables and signaling when the process is likely to be out of control (i.e., the probability of producing defects increases given current readings). Acceptance sampling plans also use conditional probability to decide whether to accept or reject a batch of products based on the number of defects found in a sample. By analyzing P(Defect | Test Result) or P(Batch Acceptance | Sample Quality), manufacturers can make data-driven decisions to improve processes, reduce waste, and ensure products meet required standards. This leads to significant cost savings and enhanced brand reputation.
Diagnostic Systems in Healthcare
As mentioned earlier, conditional probability is fundamental to diagnostic systems in healthcare. When a doctor interprets a medical test, they are essentially assessing P(Disease | Symptoms, Test Results). This involves considering the sensitivity of the test (P(Positive Test | Disease)), its specificity (P(Negative Test | No Disease)), and the prior probability or prevalence of the disease in the relevant population.
Modern diagnostic support systems, often powered by AI and machine learning, use complex probabilistic models that incorporate numerous variables and their conditional dependencies to assist clinicians in making more accurate diagnoses. For example, a system might estimate the probability of a patient having a specific type of infection given their symptoms, medical history, and recent lab results. This helps in prioritizing treatments and managing patient care more effectively. The careful application of conditional probability in these systems can lead to earlier and more accurate diagnoses, ultimately improving patient outcomes.
Students and professionals can find relevant courses in the Health & Medicine category on OpenCourser to learn more about medical data analysis.
Ethical Considerations in Application
While conditional probability is a powerful analytical tool, its application, particularly in automated decision-making systems and predictive modeling, raises significant ethical considerations. It is crucial for researchers and practitioners to be aware of these challenges to ensure that probabilistic systems are developed and deployed responsibly. Ignoring these aspects can lead to biased outcomes, privacy violations, and a lack of transparency, eroding public trust and potentially causing harm.
Bias Amplification in Predictive Systems
One of the most pressing ethical concerns is the potential for predictive systems, which often rely on conditional probabilities learned from historical data, to amplify existing societal biases. If the data used to train these models reflects historical discrimination (e.g., in hiring, loan applications, or criminal justice), the model may learn these biases and perpetuate or even exacerbate them. For example, if P(Loan Approval | Applicant Characteristics) is learned from data where certain demographic groups were unfairly denied loans, the model may continue this discriminatory pattern.
This occurs because the model learns correlations, including spurious ones that are proxies for protected attributes. Even if sensitive attributes like race or gender are explicitly excluded, other features might be highly correlated with them, leading to biased outcomes by proxy. Addressing bias amplification requires careful attention to data collection, feature selection, model auditing, and the development of fairness-aware machine learning techniques. It's a complex challenge that requires interdisciplinary collaboration.
A resource for understanding fairness in AI can often be found through organizations focused on technology ethics. For example, reports from the World Economic Forum often discuss the societal impact of artificial intelligence.
Privacy Concerns in Probabilistic Modeling
Probabilistic models, especially those trained on large, detailed datasets, can raise significant privacy concerns. Conditional probability models might inadvertently reveal sensitive information about individuals, even if the data is supposedly anonymized. For instance, a model predicting P(Medical Condition | Lifestyle Factors, Location) could potentially be used to infer an individual's health status with a high degree of certainty, even if their name is not directly in the dataset.
Techniques like linkage attacks, where different datasets are combined, can de-anonymize individuals and expose their private information. The development of privacy-preserving machine learning techniques, such as differential privacy and federated learning, aims to mitigate these risks. These methods add noise or structure constraints to the learning process to make it difficult to infer individual data points from the model's outputs. Balancing the utility of probabilistic models with the fundamental right to privacy is an ongoing challenge for researchers and policymakers.
Transparency Challenges in Complex Models
Many modern systems using conditional probability, especially deep learning models, are often described as "black boxes." While they may achieve high predictive accuracy, their internal workings and the exact reasons for a specific prediction (e.g., why P(X|Y) is a certain value) can be opaque even to their developers. This lack of transparency poses a significant ethical challenge, particularly when these models are used in high-stakes decisions like medical diagnosis, parole recommendations, or autonomous vehicle control.
If a model denies someone a loan or flags them as a high risk, the affected individual has a right to understand the reasoning. Without transparency, it's difficult to identify and correct errors, biases, or unintended consequences. The field of eXplainable AI (XAI) is dedicated to developing methods that make these complex models more interpretable, allowing humans to understand, trust, and effectively manage AI systems. This includes techniques to highlight which input features most influenced a particular conditional probability estimate.
Regulatory Compliance Frameworks
As the use of probabilistic systems becomes more pervasive, regulatory bodies worldwide are beginning to establish frameworks to govern their development and deployment. Regulations like the European Union's General Data Protection Regulation (GDPR) include provisions related to automated decision-making and the right to an explanation. Other emerging AI-specific regulations are also considering requirements for fairness, transparency, and accountability in AI systems.
Compliance with these frameworks requires organizations to understand the ethical implications of their probabilistic models, conduct impact assessments, implement measures to mitigate bias, ensure data privacy, and maintain appropriate documentation. This often involves establishing internal ethics review boards, adopting codes of conduct, and engaging with external stakeholders. Navigating the evolving regulatory landscape is becoming an increasingly important aspect of working with conditional probability in applied settings. For insights into these frameworks, publications from institutions like The Brookings Institution can be very informative.
Formal Education Pathways
For individuals aiming to build a strong theoretical and practical understanding of conditional probability, pursuing formal education is a well-established route. Universities and academic institutions offer a range of programs and courses that cover the mathematical underpinnings and diverse applications of probability theory. This path is particularly relevant for those considering careers in research, advanced data analysis, or fields requiring rigorous quantitative skills.
OpenCourser can be a valuable tool for students looking to supplement their formal education or explore specific topics in greater depth. The platform allows you to browse through mathematics courses from various providers.
These courses cover foundational and advanced probability and statistics, suitable for those on a formal education path.
These texts are often used in university courses and provide comprehensive coverage suitable for formal study.
Relevant Undergraduate Mathematics Courses
A solid foundation in undergraduate mathematics is typically the starting point. Key courses often include Calculus (I, II, and often Multivariable Calculus), as limits, series, and integration are fundamental to continuous probability distributions. Linear Algebra is also crucial, especially for understanding multivariate statistics and the geometric interpretation of data, which becomes important in machine learning applications that use probabilistic models.
Most directly, an introductory course in Probability and Statistics is essential. Such courses usually cover basic probability concepts, axioms of probability, discrete and continuous random variables, expected values, variance, and, critically, conditional probability and Bayes' theorem. Some universities offer separate, more focused courses on Probability Theory, which delve deeper into the mathematical structure of probability spaces, different types of convergence, and foundational theorems like the Law of Large Numbers and the Central Limit Theorem. A course in Discrete Mathematics can also be beneficial as it often covers combinatorics, which is essential for calculating probabilities in many scenarios.
These introductory courses are designed to build foundational skills in probability, which are essential for undergraduate studies.
Graduate Programs Emphasizing Probabilistic Modeling
For those seeking deeper expertise, graduate programs in Statistics, Data Science, Machine Learning, Applied Mathematics, or certain subfields of Computer Science and Engineering often have a strong emphasis on probabilistic modeling. Master's and Ph.D. programs in Statistics typically offer advanced courses in Probability Theory (often measure-theoretic), Statistical Inference (covering Bayesian and frequentist approaches), Stochastic Processes, and specialized topics like Time Series Analysis or Spatial Statistics, all of which build heavily on conditional probability.
Data Science and Machine Learning programs will include courses on probabilistic graphical models, Bayesian methods in machine learning, reinforcement learning, and natural language processing, where conditional probability is a core concept for model building and inference. Programs in Operations Research or Financial Engineering also rely heavily on probabilistic modeling for optimization under uncertainty and risk management. When choosing a graduate program, it's advisable to look at the research interests of the faculty and the specific courses offered in probabilistic methods.
These books are often found in graduate-level curricula and are excellent resources for advanced study.
Research Opportunities in Applied Statistics
Formal education, particularly at the graduate level, often opens doors to research opportunities in applied statistics. Conditional probability is at the heart of many research problems across diverse fields. For example, in biostatistics, researchers develop models to assess P(Disease Progression | Treatment, Genetic Markers). In environmental science, models might estimate P(Extreme Weather Event | Climate Change Indicators). In economics, researchers might study P(Recession | Financial Market Signals).
These research opportunities can be found within universities, government agencies (like the Bureau of Labor Statistics which uses statistical models extensively), research institutions, and private sector R&D departments. Such roles involve developing new statistical methodologies, applying existing methods to novel problems, and interpreting the results to provide insights and inform decisions. A strong understanding of conditional probability and its extensions is indispensable for contributing to these research areas.
Cross-Disciplinary Programs
The importance of conditional probability and probabilistic reasoning is increasingly recognized across various disciplines, leading to the growth of cross-disciplinary programs. Fields like Computational Biology, Bioinformatics, Quantitative Social Science, Computational Neuroscience, and Health Informatics explicitly integrate statistical and probabilistic modeling with subject-matter expertise.
For example, a Computational Biology program might offer courses where students learn to model P(Protein Function | Gene Sequence, Cellular Environment). A Quantitative Social Science program might focus on P(Voting Behavior | Demographics, Political Campaign Exposure). These programs are designed to train researchers and practitioners who can bridge the gap between theory and application, using probabilistic tools to address complex, real-world questions in their respective domains. They often feature project-based learning and collaboration with experts from different fields, providing a rich learning environment for applying conditional probability concepts.
Exploring course collections on OpenCourser, such as those in Data Science or Bioinformatics (if available, otherwise a general search for bioinformatics), can reveal such interdisciplinary options.
Self-Directed Learning Strategies
For those who prefer a more flexible approach, are looking to supplement formal education, or are advancing their careers, self-directed learning can be an effective way to master conditional probability. With a wealth of online resources, open-source tools, and communities, learners can tailor their educational journey to their specific goals and pace. This path requires discipline and initiative but offers significant rewards in terms of skill development and practical application.
OpenCourser is an excellent resource for self-directed learners, offering a vast catalog of courses. The "Save to list" feature on OpenCourser can help you curate your own learning path, and the Learner's Guide provides tips on how to structure your learning and stay motivated.
These courses are well-suited for self-paced learning and cover various aspects of probability, from intuitive introductions to more comprehensive guides.
For self-study, these books provide accessible yet thorough explanations of probability concepts.
Recommended Prerequisite Mathematical Skills
Before diving deep into conditional probability, ensuring you have a grasp of certain prerequisite mathematical skills will make the learning process smoother and more effective. A solid understanding of basic algebra is fundamental, including manipulating equations and working with variables. Familiarity with set theory concepts – such as unions, intersections, complements, and Venn diagrams – is also very helpful, as probability often involves reasoning about sets of outcomes.
For more advanced topics, especially those involving continuous probability distributions, a foundational knowledge of calculus (specifically differentiation and integration) is necessary. Combinatorics, the study of counting, permutations, and combinations, is also highly relevant for calculating probabilities in discrete scenarios. Many introductory online courses will review these prerequisites, but dedicated refreshers on these topics can be beneficial if you feel your skills are rusty. You can find relevant courses by searching for "precalculus" or "introductory calculus" on OpenCourser.
Project-Based Learning Approaches
One of the most effective ways to solidify your understanding of conditional probability is through project-based learning. Instead of just passively consuming information, actively apply the concepts to solve real or simulated problems. Start with simple projects, like analyzing data from a coin toss or dice roll experiment to verify conditional probability rules. As your confidence grows, you can tackle more complex projects.
Consider projects like building a simple spam filter using Naive Bayes, analyzing a dataset to find interesting conditional relationships (e.g., P(Customer Churn | Usage Patterns)), or simulating a medical diagnostic scenario. Many datasets are publicly available online (e.g., on Kaggle, UCI Machine Learning Repository). Working on projects not only reinforces theoretical knowledge but also helps develop practical skills in data handling, programming (e.g., in Python or R), and interpretation of results. Documenting your projects, perhaps in a blog post or a GitHub repository, can also serve as a portfolio of your skills.
Courses that often include projects or practical exercises can be particularly valuable.
Open-Source Tools for Practical Experimentation
Several open-source tools are invaluable for experimenting with conditional probability and related concepts. Programming languages like Python and R are particularly popular in the data science and statistics communities. Python, with libraries such as NumPy (for numerical operations), Pandas (for data manipulation), Scikit-learn (for machine learning, including Naive Bayes classifiers), and Pgmpy (for probabilistic graphical models), provides a rich ecosystem for implementing and exploring probabilistic models.
R is a language specifically designed for statistical computing and graphics. It has extensive packages for probability distributions, statistical modeling, and Bayesian analysis (e.g., Stan, JAGS via R interfaces). Using these tools, you can simulate experiments, calculate conditional probabilities from data, build and test predictive models, and visualize probabilistic relationships. Many online tutorials and courses are available to help you get started with these tools, often focusing on practical applications of probability and statistics.
Professional Certification Options
While conditional probability itself is a concept rather than a distinct field for certification, many professional certifications in data science, analytics, and machine learning require a strong understanding of it. For example, certifications offered by various software vendors or industry organizations in areas like Business Analytics, Data Engineering, or AI Engineering will often test your knowledge of underlying statistical principles, including conditional probability.
Some universities and online learning platforms also offer certificates for completing specialized tracks or series of courses in data science or statistics. While these certificates may not be formal accreditations, they can demonstrate to potential employers that you have undertaken structured learning in the field and have acquired specific skills. When considering certifications, look for those that are well-recognized in your target industry and that emphasize practical application and project work, as this will be more valuable than purely theoretical credentials.
For career-focused individuals, supplementing learning with certifications can be beneficial. OpenCourser's Learner's Guide offers insights on how to add certificates to your resume or LinkedIn profile.
Career Progression and Roles
A strong grasp of conditional probability is not just an academic pursuit; it's a highly valuable skill that underpins numerous roles across various industries. As organizations increasingly rely on data to make decisions, professionals who can understand, interpret, and apply probabilistic reasoning are in high demand. The career paths are diverse, offering opportunities for growth, specialization, and leadership in data-driven environments.
The job outlook for roles requiring strong analytical and statistical skills, such as Data Scientists and Machine Learning Engineers, is generally very positive. According to the U.S. Bureau of Labor Statistics, employment for data scientists is projected to grow significantly faster than the average for all occupations. For instance, the Occupational Outlook Handbook for Data Scientists projects a 35% growth from 2022 to 2032. Similarly, roles related to computer and information research scientists, which include many machine learning engineers, also show strong growth projections. Salaries in these fields are typically competitive, reflecting the demand for these specialized skills.
Entry-Level Positions Requiring Probabilistic Skills
For those starting their careers, several entry-level positions require a foundational understanding of conditional probability. Roles such as Junior Data Analyst, Business Intelligence Analyst, Research Assistant (in quantitative fields), or Marketing Analyst often involve working with data, identifying trends, and making basic probabilistic inferences. For instance, a marketing analyst might examine P(Purchase | Clicked on Ad) to evaluate campaign effectiveness. A business intelligence analyst might look at P(Project Delay | Resource Shortage) to identify risks.
In these roles, individuals might use tools like Excel with statistical functions, SQL for data querying, and basic data visualization tools to communicate findings. While deep theoretical knowledge might not be the primary focus, the ability to think probabilistically and understand concepts like A/B testing (which relies on comparing conditional probabilities of outcomes under different conditions) is highly valued. These positions often serve as a stepping stone to more advanced roles as individuals gain experience and further develop their analytical skills.
Foundational courses in statistics and data analysis are key for these roles.
Mid-Career Specialization Paths
As professionals gain experience, they can specialize in areas that more intensively utilize conditional probability. Data Scientist is a prominent mid-career role where conditional probability is central to building predictive models, performing statistical inference, and designing experiments. Machine Learning Engineers also rely heavily on it to develop, train, and deploy algorithms for tasks like classification, regression, and recommendation systems.
Other specialization paths include Quantitative Analyst ("Quant") in finance, who builds models for trading, risk management, and derivative pricing based on P(Market Movement | Various Factors). Actuaries use conditional probabilities extensively to assess and manage insurance and financial risks, calculating P(Claim | Insured's Profile, Event Type). Biostatisticians apply these concepts in clinical trials and epidemiological studies. These roles typically require a deeper mathematical understanding and often advanced degrees or specialized certifications.
These courses delve into the specialized areas where conditional probability is heavily applied.
Leadership Roles in Data-Driven Organizations
With significant experience and a proven track record, individuals skilled in probabilistic reasoning can move into leadership roles within data-driven organizations. Positions such as Chief Data Scientist, Director of Analytics, Head of AI, or VP of Data Science involve setting the strategic direction for data initiatives, leading teams of analysts and scientists, and ensuring that insights derived from probabilistic models translate into business value.
In these roles, while day-to-day modeling might be less frequent, a deep understanding of conditional probability and its implications (including ethical considerations like bias and fairness) is crucial for guiding technical teams, evaluating the validity of models, communicating complex findings to non-technical stakeholders, and making high-stakes decisions based on probabilistic information. Leadership also involves fostering a data-literate culture within the organization and staying abreast of new methodologies and technologies in the field.
Emerging Hybrid Roles Across Industries
The increasing pervasiveness of data is leading to the emergence of hybrid roles that combine domain expertise with strong analytical and probabilistic skills. For example, in healthcare, we see roles like Clinical Data Scientist, who combines medical knowledge with data science techniques. In urban planning, a "Smart City Analyst" might use probabilistic models to optimize traffic flow or resource allocation based on P(Congestion | Time, Events).
In journalism, "Data Journalists" use statistical analysis, including conditional probability, to uncover stories and present data-driven narratives. In manufacturing, a "Predictive Maintenance Engineer" might use sensor data to calculate P(Equipment Failure | Operating Conditions) to schedule maintenance proactively. These hybrid roles require not only the technical ability to work with probabilities but also the contextual understanding to apply these concepts effectively within a specific industry. This trend highlights the growing need for professionals who can bridge the gap between data and domain-specific challenges.
Common Misconceptions and Challenges
Conditional probability, while a powerful concept, is also prone to misinterpretation and presents certain cognitive and computational challenges. Understanding these common pitfalls is crucial for anyone working with probabilistic information, as errors in reasoning can lead to flawed conclusions and poor decisions. This section addresses some of the frequent misunderstandings and difficulties encountered when dealing with conditional probability.
Courses that emphasize intuitive understanding can help clarify these often-confused concepts.
Confusion with Joint Probability
One common area of confusion is distinguishing conditional probability P(A|B) from joint probability P(A∩B). Joint probability refers to the probability of two events A and B both occurring. Conditional probability, on the other hand, is the probability of event A occurring given that event B has already occurred. The key difference lies in the sample space being considered. For joint probability, the sample space is all possible outcomes. For conditional probability P(A|B), the sample space is reduced to only those outcomes where B is true.
For example, if we roll a fair six-sided die:
- The joint probability of rolling an even number (A) AND rolling a number greater than 3 (B) is P(A∩B). The outcomes satisfying this are {4, 6}, so P(A∩B) = 2/6 = 1/3.
- The conditional probability of rolling an even number (A) GIVEN that we've rolled a number greater than 3 (B) is P(A|B). The outcomes where B is true are {4, 5, 6}. Among these, the even numbers are {4, 6}. So, P(A|B) = 2/3.
It's essential to remember the formula P(A|B) = P(A∩B) / P(B), which clearly shows that conditional and joint probabilities are related but distinct concepts.
Base Rate Fallacy Examples
The base rate fallacy is a cognitive error where people tend to ignore the base rate (or prior probability) of an event and focus instead on specific, often new, information (the likelihood). This can lead to significantly flawed judgments, especially when interpreting conditional probabilities like those in medical diagnoses or legal settings.
Consider a classic example: A test for a rare disease (affecting 1 in 10,000 people) is 99% accurate (i.e., P(Positive Test | Disease) = 0.99 and P(Negative Test | No Disease) = 0.99, implying P(Positive Test | No Disease) = 0.01). If a randomly selected person tests positive, what is the probability they actually have the disease, P(Disease | Positive Test)? Many people intuitively think the probability is high, around 99%. However, using Bayes' theorem and accounting for the low base rate: P(Disease) = 0.0001 P(No Disease) = 0.9999 P(Positive Test | Disease) = 0.99 P(Positive Test | No Disease) = 0.01 P(Positive Test) = P(Positive Test | Disease)P(Disease) + P(Positive Test | No Disease)P(No Disease) = (0.99 * 0.0001) + (0.01 * 0.9999) = 0.000099 + 0.009999 ≈ 0.010098 P(Disease | Positive Test) = [P(Positive Test | Disease) * P(Disease)] / P(Positive Test) = (0.99 * 0.0001) / 0.010098 ≈ 0.000099 / 0.010098 ≈ 0.0098 or 0.98%. Despite a positive test from a 99% accurate test, the probability of having the disease is less than 1%! This is because the number of false positives from the large healthy population outweighs the true positives from the small diseased population. Failing to consider the base rate leads to a gross overestimation of the conditional probability.
Cognitive Biases in Interpretation
Beyond the base rate fallacy, several other cognitive biases can affect the interpretation of conditional probabilities. The "prosecutor's fallacy" is one such bias, where the conditional probability of finding evidence given innocence, P(Evidence | Innocent), is confused with the probability of innocence given the evidence, P(Innocent | Evidence). These are not the same. A small P(Evidence | Innocent) does not necessarily mean a small P(Innocent | Evidence), especially if the prior probability of innocence is high.
Another related issue is the "confusion of the inverse." People often mistakenly assume that P(A|B) is approximately equal to P(B|A). For example, the probability that a person who has a certain symptom has a particular disease, P(Disease | Symptom), is often confused with the probability that a person with the disease will exhibit that symptom, P(Symptom | Disease). These can be very different values, as demonstrated by Bayes' theorem. Awareness of these cognitive traps is the first step toward mitigating their impact on decision-making.
Computational Complexity Issues
While the basic formula for conditional probability is simple, its application in real-world scenarios, especially those involving many variables, can lead to computational challenges. Calculating joint probabilities P(A∩B) or marginal probabilities P(B) for high-dimensional data can be very complex. For instance, in Bayesian networks with many nodes, exact inference (calculating conditional probabilities) can be NP-hard, meaning the computation time can grow exponentially with the size of the network.
This has led to the development of various approximation algorithms, such as Markov Chain Monte Carlo (MCMC) methods (like Gibbs sampling or Metropolis-Hastings) and variational inference techniques. These methods allow for the estimation of conditional probabilities in complex models where exact calculation is infeasible. Understanding the trade-offs between accuracy and computational cost is an important aspect of applying conditional probability in advanced machine learning and statistical modeling.
Courses focusing on the science of uncertainty and data often touch upon these complexities.
Emerging Trends and Future Directions
The field of conditional probability, while foundational, continues to evolve with new theoretical developments and applications driven by advancements in technology and interdisciplinary research. As we generate and encounter increasingly complex data, the need for sophisticated probabilistic reasoning is growing, pushing the boundaries of what's possible. Researchers and industry strategists are exploring several exciting frontiers that promise to shape the future of how we understand and utilize conditional probability.
Quantum Probability Developments
One of the more abstract but potentially transformative areas is the exploration of quantum probability. Unlike classical probability theory where probabilities are non-negative real numbers, quantum probability involves complex numbers called probability amplitudes. The square of the modulus of these amplitudes gives the probability of an outcome. Quantum systems exhibit phenomena like superposition and entanglement, which lead to probabilistic behaviors that don't always conform to classical conditional probability rules (e.g., Bell's theorem highlights departures from local realism).
While direct applications to everyday conditional probability problems are still nascent, research in quantum probability is crucial for understanding quantum mechanics and developing quantum computing and quantum information theory. As quantum technologies mature, the unique ways conditional probabilities manifest in quantum systems could lead to new paradigms for computation and communication, particularly in areas like secure communication or specialized simulations where quantum effects are dominant. This is a highly theoretical area, primarily of interest to physicists and specialized mathematicians.
AI Explainability Requirements
As artificial intelligence systems, many of which rely on complex conditional probability models (like deep neural networks), become more integrated into critical decision-making processes (e.g., in healthcare, finance, autonomous systems), the demand for AI explainability (XAI) is rapidly increasing. Stakeholders, including users, regulators, and developers, need to understand why an AI system makes a particular prediction or decision, which often translates to understanding the conditional probabilities driving the outcome (e.g., P(Outcome | Input Features)).
Future developments will focus on creating more inherently interpretable probabilistic models or developing post-hoc explanation techniques that can accurately articulate the reasoning behind a model's output in terms of conditional dependencies and feature importance. This is not just a technical challenge but also a human-computer interaction problem: how to present complex probabilistic information in a way that is understandable and actionable for humans. The goal is to move beyond "black box" models to systems where the conditional logic is transparent and trustworthy.
The fields of Artificial Intelligence and Machine Learning Interpretability are central to this trend.
Real-Time Adaptive Systems
Many modern systems need to operate and make decisions in real-time based on streaming data. Think of autonomous vehicles reacting to changing road conditions, financial trading algorithms responding to market fluctuations, or personalized recommendation engines updating suggestions based on immediate user interactions. These systems heavily rely on the ability to update conditional probabilities dynamically and rapidly as new information arrives.
Future trends will involve developing more efficient algorithms for real-time Bayesian updating, online learning for probabilistic models, and architectures that can handle high-velocity data streams while maintaining accurate conditional probability estimates. Concepts from stochastic processes and reinforcement learning, where an agent learns P(Optimal Action | Current State, Past Experience), will be increasingly important. The challenge lies in creating systems that are not only fast but also robust and able to adapt to non-stationary environments where underlying probability distributions might change over time.
Courses on topics like streaming analytics or real-time data processing would be relevant here.
Cross-Disciplinary Research Frontiers
The power of conditional probability as a tool for reasoning under uncertainty is driving its application into ever more diverse research frontiers. We are seeing increased cross-pollination of ideas between statistics, computer science, and various scientific and engineering disciplines. For example, in systems biology, researchers are building complex probabilistic models of cellular pathways, trying to understand P(Cellular Response | Combination of Signals). In climate science, efforts are focused on improving probabilistic forecasts of P(Extreme Event | Climate Model, Emission Scenario).
Cognitive science is another area where probabilistic models of brain function are gaining traction, attempting to explain perception and decision-making as forms of Bayesian inference, i.e., the brain calculating P(State of World | Sensory Input). These interdisciplinary efforts often require the development of novel probabilistic modeling techniques tailored to the specific challenges and data types of each field. The future will likely see even more sophisticated applications of conditional probability as researchers tackle increasingly complex systems.
Books on causality and stochastic processes can provide insight into these advanced research areas.
Frequently Asked Questions (Career Focus)
For those considering careers that leverage conditional probability, or looking to enhance their existing skill set, several common questions arise. This section aims to address these practical concerns, providing insights for career-oriented readers navigating the landscape of opportunities related to this fundamental concept.
What are essential skills for roles involving conditional probability?
Beyond a solid mathematical understanding of conditional probability itself, Bayes' theorem, and related concepts, several other skills are essential. Strong analytical and problem-solving abilities are paramount. You need to be able to translate real-world problems into a probabilistic framework. Proficiency in programming languages commonly used for data analysis, such as Python or R, is often required, along with experience with relevant libraries for statistical modeling and machine learning (e.g., Scikit-learn, Pgmpy, Stan).
Data manipulation and cleaning skills are also crucial, as real-world data is rarely perfect. The ability to effectively visualize and communicate probabilistic findings to both technical and non-technical audiences is highly valued. Furthermore, domain knowledge in the specific industry you're targeting (e.g., finance, healthcare, tech) can be a significant advantage, as it helps in understanding the context and relevance of the probabilistic models you build. Finally, a mindset of continuous learning is important, as new techniques and tools are constantly emerging.
Many courses aim to build these essential skills.
In which industries is there the highest demand for conditional probability skills?
Demand for skills in conditional probability is widespread, but certain industries show particularly high demand. The technology sector is a major employer, with roles in data science, machine learning, and AI research at companies developing search engines, social media platforms, e-commerce sites, and software services. Conditional probability is key to features like recommendation systems, fraud detection, and natural language understanding.
The finance and insurance industries also heavily rely on these skills for risk assessment, algorithmic trading, credit scoring, and actuarial science. Healthcare is another rapidly growing area, with applications in medical diagnosis, bioinformatics, epidemiological modeling, and personalized medicine. Furthermore, consulting firms often seek individuals with strong probabilistic modeling skills to help clients across various sectors solve data-driven problems. Marketing and advertising use conditional probability for customer segmentation, campaign optimization, and churn prediction.
What are some career transition strategies for individuals from non-math fields?
Transitioning from a non-math field into a role that heavily utilizes conditional probability requires a structured approach. Start by building a strong foundational understanding of mathematics, focusing on algebra, basic calculus, and, most importantly, introductory probability and statistics. Online courses are an excellent resource for this, allowing you to learn at your own pace. OpenCourser's browse page can help you find suitable introductory courses in mathematics and statistics.
Next, gain practical skills by working on projects using real-world datasets and common data analysis tools like Python or R. Focus on projects that are relevant to your target industry or that showcase your ability to apply probabilistic thinking. Consider creating a portfolio of your projects to demonstrate your skills to potential employers. Networking with professionals in your target field can provide valuable insights and potential opportunities. Finally, be prepared to start in an entry-level or junior role to gain experience, and emphasize your unique domain knowledge from your previous field as a complementary asset.
For those transitioning, starting with intuitive introductions can be very helpful.
Are there freelance or consulting opportunities related to conditional probability?
Yes, there are certainly freelance and consulting opportunities for individuals with expertise in conditional probability and its applications, particularly in areas like data science, statistical modeling, and machine learning. Small and medium-sized businesses that may not have the resources to hire full-time data scientists often seek consultants for specific projects, such as developing predictive models, analyzing customer data, or providing statistical expertise for research.
Experienced professionals can offer services like building custom risk models for financial clients, developing A/B testing frameworks for marketing agencies, or providing statistical consulting for academic researchers. Success in freelancing or consulting in this space typically requires not only strong technical skills but also excellent communication, project management abilities, and a knack for understanding and solving business problems. Building a strong professional network and a portfolio of successful projects is key to attracting clients.
How is the impact of AI automation on roles requiring conditional probability skills?
AI and automation are indeed transforming many roles, including those involving conditional probability. Some routine tasks involving basic data analysis or the application of standard probabilistic models might become more automated. However, this doesn't necessarily mean a reduction in demand for skilled professionals. Instead, the nature of the roles is likely to evolve.
AI tools can automate parts of the modeling pipeline, freeing up professionals to focus on more complex aspects such as problem formulation, interpreting results in a business context, ensuring ethical considerations (like fairness and bias mitigation) are addressed, and developing novel applications of probabilistic methods. The demand for individuals who can design, oversee, and critically evaluate these AI systems, and who can solve problems that are too nuanced or novel for current automation, is likely to increase. Therefore, while some tasks may be automated, the need for deep understanding and critical thinking around conditional probability will remain crucial, especially for developing and managing these advanced AI systems.
Are there significant global market differences in opportunities?
Yes, there can be significant global market differences in opportunities for roles requiring conditional probability skills. Major technology hubs and financial centers, such as Silicon Valley, New York, London, Singapore, and increasingly cities in India and China, often have a high concentration of relevant job openings due to the presence of large tech companies, financial institutions, and a vibrant startup ecosystem.
However, the demand for data science and analytics skills is growing globally across many countries and industries as more organizations embrace data-driven decision-making. The specific types of roles and industries in demand may vary by region. For example, one region might have more opportunities in manufacturing analytics, while another might focus on e-commerce or healthcare AI. Factors like government investment in AI and data science, the maturity of the local tech industry, and the presence of universities with strong research programs in these areas can all influence the job market. Remote work opportunities have also expanded the geographic reach for some roles, though this varies.
Understanding conditional probability is more than an academic exercise; it is a vital skill for navigating and shaping our increasingly data-centric world. Whether you are aiming for a career in cutting-edge technology, seeking to solve complex problems in science or finance, or simply wish to become a more discerning consumer of information, a grasp of conditional probability offers profound benefits. The journey to mastering it can be challenging, requiring dedication and practice, but the ability to reason effectively about uncertainty is an invaluable asset in any endeavor.