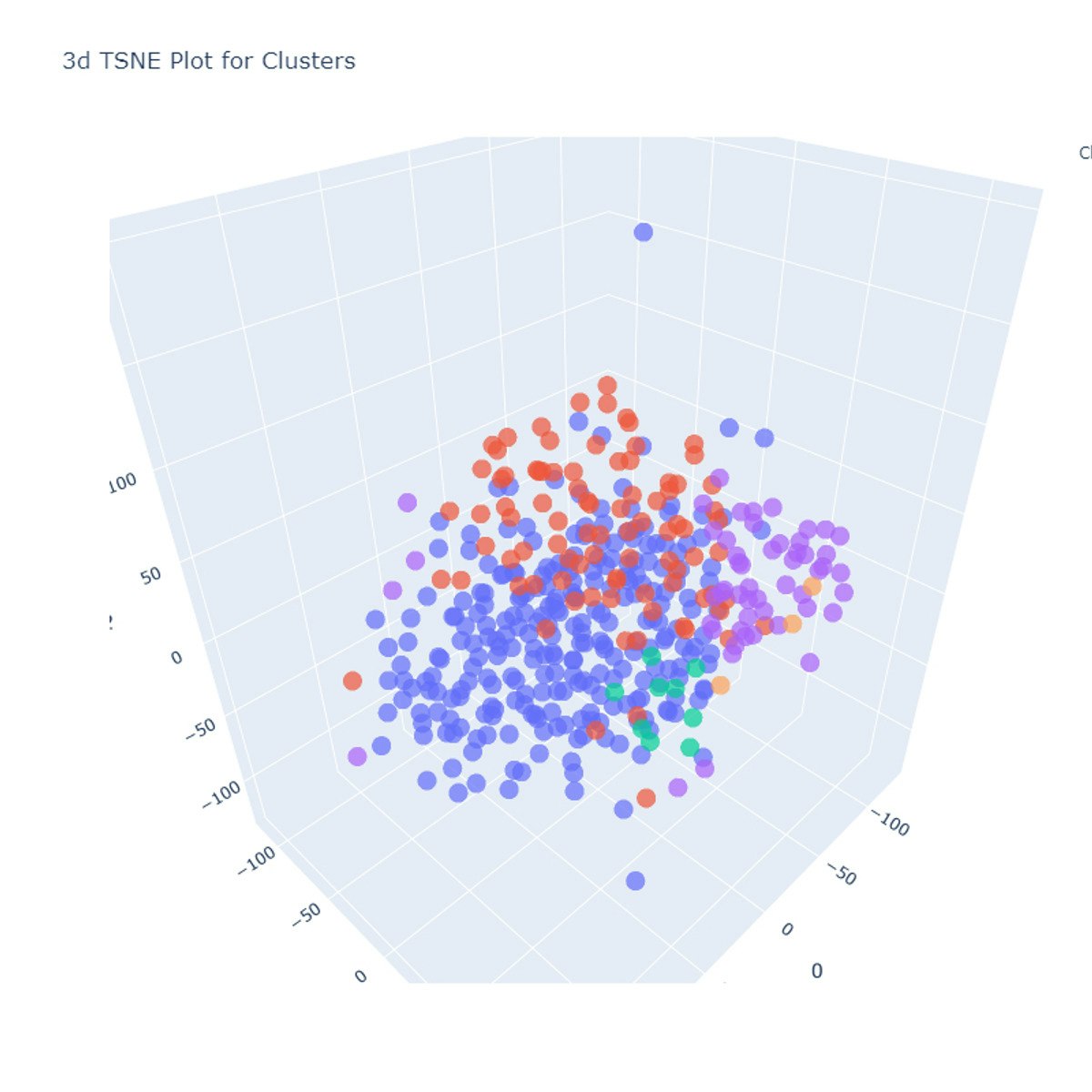
Clustering
Introduction to Clustering
Clustering is a fundamental technique in the field of data analysis and machine learning. At its core, clustering involves grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar to each other than to those in other groups. It's a form of unsupervised learning, meaning it doesn't rely on pre-labeled data; instead, it seeks to discover inherent structures and patterns within the data itself. Think of it like sorting a mixed bag of fruits into piles of apples, oranges, and bananas based purely on their characteristics, without knowing their names beforehand.
The power of clustering lies in its ability to reveal hidden relationships and categorize complex datasets automatically. This makes it an exciting tool for discovery across many fields. Imagine automatically identifying distinct customer segments from purchase histories to tailor marketing campaigns, or grouping similar genes based on expression patterns to understand biological functions better. The process of uncovering these underlying groups can lead to significant insights and data-driven decisions.
What is Clustering?
Definition and Core Purpose
Clustering is the task of dividing a population or data points into a number of groups such that data points in the same groups are more similar to other data points in the same group and dissimilar to the data points in other groups. It is essentially a collection of objects based on similarity and dissimilarity between them. The primary goal is to partition data points into distinct subgroups where the members within each subgroup share common traits or proximity according to some defined measure.
This technique is widely used for exploratory data analysis to get an initial understanding of the data distribution. Unlike classification (a supervised learning task), clustering operates without prior knowledge of the group definitions. It aims to find these groups organically from the data. The effectiveness of clustering often depends heavily on the chosen similarity measure and the algorithm used.
Consider sorting laundry. You might group clothes by color (whites, darks, colors) or by fabric type (cotton, synthetics, delicates) or by owner. Each sorting method represents a different clustering approach, based on different "similarity" criteria. Clustering algorithms do something similar, but with data points in a mathematical space, using distance or similarity functions to decide which points belong together.
Historical Context and Evolution
The roots of clustering can be traced back to fields like statistics, anthropology, and biology in the early 20th century, where researchers sought methods to classify objects or organisms based on observed characteristics. Early methods were often manual or based on simple statistical measures. The advent of computers dramatically accelerated the development and application of clustering algorithms.
In the mid-20th century, foundational algorithms like hierarchical clustering and partitioning methods (such as k-means, formally proposed later but with roots in earlier work) began to emerge. These methods provided systematic ways to group data points computationally. The development was driven by needs in numerical taxonomy, psychology, and market research.
The rise of computer science, particularly in areas like pattern recognition and machine learning from the 1960s onwards, further propelled clustering research. New algorithms addressing limitations like scalability, handling different data types, and discovering clusters of arbitrary shapes (like DBSCAN) were developed. Today, clustering is a cornerstone of Data Science and Artificial Intelligence, constantly evolving with advancements in algorithms, computing power, and the increasing volume and complexity of data.
Key Industries and Applications
Clustering finds applications across a vast array of industries due to its versatility in pattern discovery. In marketing, it's used for customer segmentation, identifying groups of customers with similar purchasing behaviors or demographics for targeted advertising. Retailers use it for basket analysis, discovering items frequently bought together to optimize store layouts and promotions.
In finance, clustering helps in identifying groups of stocks with similar price movements for portfolio diversification and risk management. It's also employed in fraud detection by identifying unusual patterns or outliers that deviate significantly from normal transaction clusters. Biology and medicine leverage clustering extensively, for instance, in genomics to group genes with similar expression profiles, in medical imaging to segment tissues, and in epidemiology to identify disease outbreak hotspots.
Furthermore, clustering is crucial in information retrieval and natural language processing for organizing documents, grouping search results, and identifying topics in large text corpora. Social network analysis uses clustering to find communities or groups of interconnected users. Urban planning might use it to group neighborhoods based on socio-economic factors or land use patterns.
These courses offer a broad introduction to machine learning concepts, including clustering:
Basic Types of Clustering
Clustering algorithms can be broadly categorized based on their underlying approach. Partitional clustering algorithms divide the dataset into a predetermined number of non-overlapping clusters. The most famous example is K-means, which iteratively assigns points to the nearest cluster center (centroid) and recalculates the centroids.
Hierarchical clustering algorithms build a hierarchy of clusters, either agglomerative (bottom-up), starting with individual points and merging clusters, or divisive (top-down), starting with the whole dataset and splitting clusters. The result is often visualized as a dendrogram, showing the nested structure of clusters.
Density-based clustering algorithms connect areas of high data point density into clusters, allowing for the discovery of arbitrarily shaped clusters and the identification of noise points (outliers) in low-density regions. DBSCAN is a well-known example. Other types include grid-based methods, which quantize the space into cells, and model-based methods, which assume clusters follow certain statistical distributions (like Gaussian Mixture Models).
Key Concepts and Terminology
Distance Metrics
The notion of "similarity" or "dissimilarity" between data points is fundamental to clustering. This is typically quantified using a distance metric. The choice of metric significantly impacts the resulting clusters as it defines what it means for points to be "close" or "far apart."
Commonly used distance metrics include Euclidean distance, which is the straight-line distance between two points in Euclidean space (think Pythagorean theorem generalized to multiple dimensions). Manhattan distance (or city block distance) measures the distance by summing the absolute differences of their coordinates, like navigating a grid city. For high-dimensional data, especially text data represented as vectors, Cosine similarity is often preferred; it measures the cosine of the angle between two vectors, focusing on orientation rather than magnitude.
Other metrics exist for different data types, such as Hamming distance for categorical data or Jaccard index for sets. Selecting an appropriate distance metric requires understanding the nature of the data and the specific goals of the clustering task. An inappropriate metric can lead to meaningless clusters.
For those less familiar with these concepts, imagine you have three locations on a map: your home, the grocery store, and the park. Euclidean distance is like drawing a straight line ("as the crow flies") between them. Manhattan distance is like driving along the streets, assuming a perfect grid layout – you can only move horizontally and vertically. Cosine similarity is a bit different; it's less about the distance and more about the direction. If two vectors point in roughly the same direction, they are considered similar, regardless of how long they are.
Centroids, Dendrograms, and Cluster Validation
Several key terms appear frequently when discussing clustering. A centroid typically represents the center point of a cluster, often calculated as the mean of all the data points belonging to that cluster. It's a central concept in algorithms like K-means, where clusters are defined around these centroids.
A dendrogram is a tree diagram used to visualize the output of hierarchical clustering. It illustrates the arrangement of the clusters produced by the corresponding analyses, showing how clusters are merged (agglomerative) or split (divisive) at different levels of similarity. Cutting the dendrogram at a certain height determines the final number of clusters.
Cluster validation refers to the process of evaluating the quality and reliability of the clusters produced by an algorithm. Since clustering is unsupervised, there's often no single "correct" answer. Validation techniques can be internal (using information inherent to the data, like silhouette score or Davies-Bouldin index), external (comparing results to known ground truth labels, if available), or relative (comparing results from different algorithms or parameter settings).
Density vs. Distribution-based Approaches
Clustering algorithms can also be differentiated by how they define a cluster. Density-based methods, like DBSCAN, define clusters as dense regions of data points separated by sparser regions. These methods excel at finding non-spherical clusters and handling noise, as they don't force points into clusters if they reside in low-density areas.
Distribution-based methods, such as Gaussian Mixture Models (GMMs), assume that data points within a cluster are generated from a specific probability distribution (often a Gaussian or normal distribution). The goal is to find the parameters of these distributions that best fit the data. GMMs allow for "soft clustering," where points can belong to multiple clusters with varying probabilities, reflecting uncertainty in cluster assignments.
The choice between these approaches depends on assumptions about the data structure. If clusters are expected to be dense and potentially irregular in shape, density-based methods might be suitable. If data is believed to follow certain statistical distributions, model-based approaches like GMMs could be more appropriate.
Curse of Dimensionality
The Curse of Dimensionality refers to various phenomena that arise when analyzing data in high-dimensional spaces (i.e., data with many features or attributes). As the number of dimensions increases, the volume of the space grows exponentially, causing data points to become sparse.
In the context of clustering, this sparsity makes distance metrics less meaningful. In high dimensions, the distance between any two points can become surprisingly similar, making it difficult to distinguish close neighbors from distant ones. This challenges many traditional clustering algorithms that rely heavily on distance calculations.
Furthermore, many dimensions may be irrelevant or noisy, obscuring the underlying cluster structure present in a subset of relevant dimensions. Techniques like dimensionality reduction (e.g., Principal Component Analysis or PCA) or feature selection are often necessary pre-processing steps when dealing with high-dimensional data before applying clustering algorithms.
These courses delve into high-dimensional data analysis and related statistical learning concepts:
This classic text provides a deep dive into statistical learning, including clustering and dimensionality issues:
Common Clustering Algorithms and Techniques
K-means: Use Cases, Strengths, and Limitations
K-means is arguably the most popular and widely used partitional clustering algorithm. It aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean (cluster center or centroid), serving as a prototype of the cluster. It's computationally efficient and relatively simple to implement.
Its strengths lie in its speed and scalability to large datasets. K-means works well when clusters are roughly spherical, well-separated, and balanced in size. Common use cases include initial data exploration, feature engineering, and market segmentation where distinct, globular groups are expected.
However, K-means has limitations. The user must specify the number of clusters (k) beforehand, which isn't always known. It's sensitive to the initial placement of centroids and can converge to suboptimal solutions. K-means struggles with clusters of varying sizes, different densities, and non-convex (non-spherical) shapes. It's also sensitive to outliers, which can significantly distort the position of centroids.
DBSCAN for Noise Handling and Irregular Shapes
DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is a density-based clustering algorithm. It groups together points that are closely packed together (points with many nearby neighbors), marking as outliers points that lie alone in low-density regions. Unlike K-means, DBSCAN does not require the number of clusters to be specified beforehand.
A key strength of DBSCAN is its ability to discover clusters of arbitrary shapes, as it connects dense regions regardless of their form. It's also robust to outliers, explicitly identifying them as noise points rather than forcing them into clusters. This makes it suitable for applications like anomaly detection or clustering spatial data with noise.
Limitations include its sensitivity to parameter settings (epsilon, the neighborhood radius, and MinPts, the minimum number of points required to form a dense region). Finding appropriate parameters can be challenging, especially if clusters have varying densities. DBSCAN may struggle to correctly identify clusters with significantly different densities connected together.
Hierarchical Clustering (Agglomerative/Divisive)
Hierarchical clustering creates a nested sequence of clusters. Agglomerative (bottom-up) methods start with each data point as its own cluster and iteratively merge the closest pair of clusters until only one cluster (containing all points) remains. Divisive (top-down) methods start with all points in one cluster and recursively split clusters until each point is in its own cluster.
The main advantage is that it doesn't require specifying the number of clusters upfront; the hierarchy (dendrogram) allows exploration of groupings at different levels. It can capture nested structures in the data. Different linkage criteria (e.g., single, complete, average, Ward's method) determine how the distance between clusters is calculated, influencing the final structure.
Hierarchical clustering can be computationally expensive, especially agglomerative methods which typically have quadratic time complexity, making them less suitable for very large datasets. The decisions made early in the merging (agglomerative) or splitting (divisive) process are irreversible, which can sometimes lead to suboptimal clusters.
Gaussian Mixture Models (GMMs) and Soft Clustering
Gaussian Mixture Models (GMMs) are a probabilistic, model-based clustering approach. They assume that the data is generated from a mixture of a finite number of Gaussian distributions with unknown parameters. GMMs attempt to find the parameters of these Gaussian components that best explain the observed data, typically using the Expectation-Maximization (EM) algorithm.
GMMs offer more flexibility than K-means as they can model clusters that are not spherical (ellipsoidal shapes determined by the covariance matrix of each Gaussian). A significant feature is "soft clustering": GMMs provide probabilities that each data point belongs to each cluster, rather than assigning points definitively (hard assignment). This reflects uncertainty and can be useful in many applications.
However, GMMs can be computationally intensive, especially with many components or dimensions. Like K-means, the number of Gaussian components (clusters) often needs to be specified. The assumption of Gaussian distributions might not hold for all datasets. Convergence of the EM algorithm can be sensitive to initialization and may find local optima.
These courses provide hands-on experience with various clustering algorithms:
For implementing these algorithms, consider these practical guides:
Applications of Clustering in Real-World Scenarios
Customer Segmentation in Marketing Analytics
One of the most prominent applications of clustering is in marketing analytics for customer segmentation. Businesses collect vast amounts of data about their customers, including demographics, purchase history, website interactions, and survey responses. Clustering algorithms can process this data to identify distinct groups of customers with similar characteristics or behaviors.
For example, a retailer might discover segments like "high-spending loyalists," "budget-conscious occasional shoppers," and "new customers exploring specific categories." Understanding these segments allows businesses to tailor marketing messages, product recommendations, promotions, and customer service strategies more effectively. This personalization can lead to increased customer engagement, loyalty, and ultimately, revenue.
K-means and hierarchical clustering are often used for segmentation, although GMMs can provide nuanced insights through soft assignments. The challenge lies in selecting relevant features and interpreting the resulting clusters in a meaningful business context.
Anomaly Detection in Fraud Prevention
Clustering can be adapted for anomaly or outlier detection, which is crucial in areas like fraud prevention and network security. The underlying idea is that normal data points tend to form dense clusters, while anomalies or fraudulent activities often appear as isolated points or small, sparse clusters far from the norm.
Density-based algorithms like DBSCAN are naturally suited for this, as they explicitly identify noise points. Alternatively, one can use algorithms like K-means and identify points that are very distant from any cluster centroid as potential anomalies. By modeling normal behavior through clusters, deviations can be flagged for investigation.
Financial institutions use this to detect potentially fraudulent credit card transactions that don't fit a customer's typical spending patterns. In cybersecurity, it helps identify unusual network traffic patterns that might indicate an intrusion attempt. The effectiveness depends on having a clear definition of "normal" behavior within the data.
Genomic Data Grouping in Bioinformatics
Bioinformatics heavily relies on clustering to make sense of complex biological data. In genomics, clustering helps analyze gene expression data from microarray or RNA-seq experiments. Researchers can group genes that exhibit similar expression patterns across different conditions or time points, suggesting they might be co-regulated or involved in related biological pathways.
Similarly, clustering can group patients based on their genetic profiles or disease symptoms, potentially identifying subtypes of diseases like cancer. This can lead to more personalized medicine approaches. Hierarchical clustering is frequently used for visualizing gene expression data (heatmaps with dendrograms), while various other algorithms are applied depending on the specific research question and data characteristics.
The high dimensionality and often noisy nature of biological data present significant challenges, making preprocessing and careful algorithm selection critical.
You might explore roles in this field:
Document Clustering for NLP Tasks
In Natural Language Processing (NLP), clustering is used to organize large collections of text documents. By representing documents as numerical vectors (e.g., using TF-IDF or word embeddings), clustering algorithms can group documents with similar topics or content.
This is useful for tasks like topic modeling (discovering latent themes in a corpus), organizing search engine results, detecting duplicate or near-duplicate documents, and improving information retrieval systems. For instance, a news aggregator might use clustering to group articles about the same event from different sources.
Algorithms like K-means (often with cosine similarity) and hierarchical clustering are commonly used. The challenge often lies in effective text representation and dealing with the high dimensionality and sparsity characteristic of text data.
This book covers information retrieval concepts, often involving clustering:
Challenges and Limitations of Clustering
Sensitivity to Initial Parameters and Noise
Many clustering algorithms are sensitive to their initial parameter settings. For K-means, the initial placement of centroids can significantly affect the final clusters and convergence. For DBSCAN, the choice of epsilon and MinPts determines which points are considered core points, border points, or noise, drastically altering the outcome. Selecting optimal parameters often requires domain knowledge or experimentation.
Noise and outliers in the data can also pose significant challenges. Algorithms like K-means are particularly susceptible, as outliers can pull centroids away from their "true" centers. While density-based methods like DBSCAN handle noise better, they might misclassify points in regions where density varies significantly.
Robust clustering techniques and careful data preprocessing (including outlier detection and removal, if appropriate) are often necessary to mitigate these sensitivities and obtain reliable results.
Interpretability vs. Accuracy Trade-offs
There's often a trade-off between the complexity (and potential accuracy) of a clustering model and its interpretability. Simple algorithms like K-means produce easily understandable results (points belong to the cluster with the nearest centroid), but might not capture complex structures accurately.
More sophisticated methods like GMMs or spectral clustering might provide a better fit to the data or discover more nuanced patterns, but their underlying mechanisms and results (e.g., soft assignments, complex transformations) can be harder to explain to non-experts. Hierarchical clustering offers interpretability through dendrograms, but the resulting structure can be complex.
Choosing the right balance depends on the application. In some exploratory scenarios, interpretability might be paramount, while in others, maximizing the accuracy of pattern discovery (validated through appropriate metrics) might be the priority.
Scalability Issues with Big Data
As datasets grow larger (Big Data), the computational cost of clustering algorithms becomes a major concern. Many traditional algorithms have time or memory complexity that scales poorly with the number of data points or dimensions. For instance, standard hierarchical clustering is often O(n^2 log n) or even O(n^3) in time complexity, making it infeasible for millions of data points.
While K-means is relatively scalable, its iterative nature can still be time-consuming on massive datasets. Density-based methods like DBSCAN can also face scalability challenges depending on the implementation and data distribution. Handling high dimensionality adds another layer of complexity.
Significant research focuses on developing scalable clustering algorithms. Techniques include sampling, data summarization, parallel and distributed computing frameworks (like Apache Spark), and approximate algorithms that trade some accuracy for speed. Choosing an algorithm often involves considering these scalability constraints.
Subjectivity in Cluster Evaluation Metrics
Evaluating the "quality" of a clustering result is inherently challenging and somewhat subjective because there's typically no ground truth label to compare against (as in supervised learning). Various internal validation metrics exist (e.g., Silhouette Coefficient, Davies-Bouldin Index, Calinski-Harabasz Index), but they measure different aspects of cluster cohesion and separation based on geometric properties.
Different metrics can favor different types of cluster structures (e.g., some prefer compact, spherical clusters). An algorithm might perform well according to one metric but poorly according to another. Furthermore, a statistically "good" clustering result according to these metrics might not necessarily be meaningful or useful for the specific application domain.
Ultimately, the evaluation often combines quantitative metrics with qualitative assessment based on domain expertise. Visual inspection of the clusters (if dimensionality allows) and assessing the practical utility and interpretability of the discovered groups are crucial steps in judging the success of a clustering task.
These books delve deeper into data mining concepts, including evaluation:
Formal Education Pathways
Relevant Undergraduate Courses
A strong foundation for understanding and applying clustering techniques typically begins at the undergraduate level. Core mathematical subjects are essential. Courses in Linear Algebra provide the basis for understanding vector spaces and transformations used in many algorithms. Calculus is necessary for optimization techniques involved in algorithms like K-means and GMMs.
Probability and Statistics are crucial for understanding data distributions, hypothesis testing, and model-based methods like GMMs. Courses in introductory programming, particularly in languages like Python or R, are vital for implementing and applying clustering algorithms using standard libraries.
Specific courses in Data Structures and Algorithms help in understanding the computational complexity and efficiency of different clustering methods. Introductory courses in Machine Learning or Data Mining will often cover clustering as a key topic, introducing fundamental algorithms and concepts.
Graduate Research Opportunities
Graduate studies (Master's or PhD) offer opportunities to delve deeper into the theory and application of clustering and unsupervised learning. Master's programs in Data Science, Statistics, Computer Science, or related fields often include advanced courses covering a wider range of clustering algorithms, theoretical underpinnings, and specialized applications.
Research opportunities at the graduate level might involve developing novel clustering algorithms, exploring clustering for specific data types (e.g., time series, graphs, text), investigating theoretical properties like convergence and robustness, or applying clustering to solve complex problems in domains like bioinformatics, astrophysics, or social sciences.
Working with faculty on research projects provides invaluable experience in tackling open problems, designing experiments, evaluating results rigorously, and contributing to the field's knowledge base.
PhD-Level Contributions
A PhD focused on clustering or related areas of unsupervised learning involves making significant original contributions to the field. This could take many forms: developing fundamentally new algorithms with improved performance, scalability, or ability to handle complex data structures; providing new theoretical analyses of existing methods; or pioneering novel applications of clustering in emerging scientific or technological domains.
PhD research often involves tackling challenging open questions, such as clustering in extremely high dimensions, handling streaming data, incorporating domain knowledge or constraints, developing interpretable clustering methods, or ensuring fairness and privacy in clustering results.
Successful PhD work requires deep mathematical and computational expertise, strong analytical skills, creativity, and perseverance. Contributions are typically disseminated through publications in top-tier machine learning, data mining, or domain-specific conferences and journals.
Capstone Projects Integrating Clustering
Whether at the undergraduate or graduate level, capstone projects provide an excellent opportunity to apply clustering techniques in a practical, integrated context. These projects often involve tackling a real-world problem using data analysis techniques, frequently combining clustering with other machine learning methods.
For example, a project might involve using clustering for initial customer segmentation, followed by building predictive models (classification or regression) tailored to each segment. Another project could use clustering to identify patterns in sensor data, followed by anomaly detection algorithms to flag system failures. Integrating clustering into a larger data analysis pipeline demonstrates a practical understanding of its role and limitations.
Such projects allow students to gain hands-on experience with the entire data science workflow: data acquisition, cleaning, preprocessing, feature engineering, algorithm selection and implementation (including clustering), evaluation, and interpretation of results in the context of the original problem.
These courses include project components that allow applying learned techniques:
Online Learning and Self-Study Strategies
Building Foundational Math Skills Remotely
For those pursuing clustering through self-study or transitioning careers, building the necessary mathematical foundation online is entirely feasible. Numerous online courses cover Linear Algebra, Calculus, Probability, and Statistics, often taught by instructors from top universities. These courses provide the theoretical underpinning required to grasp how clustering algorithms work.
Platforms like OpenCourser aggregate courses from various providers, making it easier to find resources tailored to your current level and learning style. Focus on understanding core concepts rather than just memorizing formulas. Working through exercises and proofs helps solidify understanding. Don't shy away from revisiting topics; mathematical maturity builds over time.
Supplementing formal courses with resources like online tutorials, interactive visualizations, and math-focused websites can provide different perspectives and reinforce learning. Consistency is key; dedicate regular time slots for studying mathematical concepts.
Open-Source Tools and Libraries
The practical application of clustering is greatly facilitated by powerful open-source tools and libraries. For Python users, scikit-learn is the cornerstone library for machine learning, offering efficient implementations of numerous clustering algorithms (K-means, DBSCAN, Hierarchical, GMM, etc.), along with tools for preprocessing, dimensionality reduction, and evaluation.
Libraries like NumPy and Pandas are essential for data manipulation and numerical operations. For visualization, Matplotlib and Seaborn are standard choices. For very large datasets, frameworks like Apache Spark (with its MLlib library) provide distributed computing capabilities. Learning to use these tools effectively is a critical skill.
Many online courses focus specifically on teaching these libraries within the context of data science and machine learning projects. Hands-on tutorials and documentation are readily available online, enabling self-learners to quickly become proficient.
These courses emphasize practical implementation, often using Python and scikit-learn:
Portfolio Projects Using Public Datasets
Theoretical knowledge and tool proficiency are best cemented through practice. Working on personal projects using publicly available datasets is an excellent way for self-learners and career pivoters to build practical skills and create a portfolio showcasing their abilities.
Numerous sources offer free datasets suitable for clustering tasks, such as Kaggle Datasets, UCI Machine Learning Repository, government open data portals, and specific domain repositories (e.g., Gene Expression Omnibus). Choose datasets that interest you and formulate a clear question or goal that clustering can help address.
Document your process thoroughly: data cleaning steps, rationale for choosing a specific algorithm and distance metric, parameter tuning experiments, evaluation methods, and interpretation of the resulting clusters. Sharing your projects on platforms like GitHub or personal blogs demonstrates initiative and practical competence to potential employers.
Blending MOOCs with Hands-on Practice
Massive Open Online Courses (MOOCs) offer structured learning paths covering clustering theory and application. Combining these courses with independent hands-on practice creates a powerful learning strategy. Use MOOCs to grasp the concepts and see guided examples, then apply what you've learned to different datasets or variations of the problems presented.
Don't just passively watch videos; actively engage with the material, complete assignments, and participate in course forums if available. Use the OpenCourser Learner's Guide for tips on maximizing your learning from online courses, structuring your self-study plan, and staying motivated.
Consider specializing by taking sequences of courses focusing on unsupervised learning or specific application domains. OpenCourser allows you to save courses to a list, helping you plan and track your learning journey. Remember that continuous learning is vital in this rapidly evolving field.
These courses provide comprehensive coverage of unsupervised learning techniques:
Career Opportunities and Progression
Entry-Level Roles
Individuals with foundational knowledge of clustering and related data analysis skills can find opportunities in entry-level roles such as Data Analyst or Junior Data Scientist. In these positions, clustering might be used for tasks like exploratory data analysis, basic customer segmentation, or identifying patterns in operational data.
Another entry point is through roles like Business Intelligence (BI) Analyst, where clustering might be used within BI tools to group data for reporting and visualization. Some Machine Learning Engineer roles might involve implementing or deploying clustering models as part of larger systems, although these often require stronger software engineering skills as well.
Success in these roles typically requires proficiency in relevant tools (SQL, Python/R, data visualization software), a good understanding of core statistical concepts, and strong communication skills to explain findings to non-technical stakeholders.
Consider exploring these career paths:
Mid-Career Specialization
With experience, professionals can specialize further in clustering and unsupervised learning. Roles like Machine Learning Engineer or Research Scientist often involve developing, implementing, and optimizing more sophisticated clustering algorithms or applying them to complex, domain-specific problems (e.g., bioinformatics, computer vision, finance).
Some may become Clustering Specialists or Unsupervised Learning Experts within data science teams, serving as consultants on projects requiring deep expertise in these techniques. This often involves staying abreast of the latest research, understanding the nuances of different algorithms, and knowing how to evaluate and validate clustering results rigorously.
Mid-career progression typically requires a deeper theoretical understanding, proven experience in applying clustering successfully to solve business or scientific problems, and often, advanced degrees (Master's or PhD) or equivalent demonstrated expertise.
Leadership and Management Roles
Experienced practitioners with strong technical backgrounds in clustering and broader machine learning, combined with leadership capabilities, can move into management roles. Positions like Data Science Manager, AI Product Manager, or Lead Research Scientist involve overseeing teams, setting technical direction, managing projects, and translating business needs into data science solutions.
In these roles, a deep understanding of clustering's capabilities and limitations is crucial for guiding strategy, allocating resources, and ensuring the responsible and effective use of these techniques. AI Product Managers specifically focused on products leveraging unsupervised learning need to understand the user needs, market opportunities, and technical feasibility related to clustering applications.
Strong communication, strategic thinking, and people management skills become increasingly important alongside technical expertise at this level.
Freelance and Consulting Opportunities
Expertise in clustering can also open doors to freelance or consulting opportunities. Businesses across various sectors often need specialized help with tasks like customer segmentation, anomaly detection, or analyzing specific types of complex data where clustering is applicable.
Freelancers or consultants might be brought in for specific projects requiring deep knowledge of particular algorithms, evaluation techniques, or domain applications. This path requires not only technical proficiency but also strong business development, project management, and client communication skills.
Building a strong portfolio of successful projects and a professional network is key to succeeding as an independent consultant in the clustering space. Niche expertise in applying clustering within specific industries (e.g., healthcare, finance, e-commerce) can be particularly valuable.
Ethical Considerations in Clustering
Bias Propagation Through Features
Clustering algorithms group data based on the features provided. If these features encode societal biases (related to race, gender, age, socio-economic status, etc.), the resulting clusters can inadvertently reflect and potentially amplify these biases. For example, clustering loan applicants based on features that correlate with protected characteristics might lead to discriminatory outcomes, even if protected attributes themselves are excluded.
It is crucial to carefully select and scrutinize the features used for clustering, considering their potential to carry bias. Auditing clustering results for fairness across different demographic groups is an important step, although defining and measuring fairness in unsupervised settings remains an active area of research.
Techniques for bias mitigation in clustering are emerging but require careful consideration of the specific context and potential harms.
Privacy Risks in Demographic Clustering
Clustering individuals based on demographic, behavioral, or personal data raises significant privacy concerns. While the goal might be benign (e.g., targeted marketing), the creation of detailed profiles for groups of individuals can feel intrusive or be used for potentially harmful purposes like discriminatory pricing or exclusion from opportunities.
Even if data is anonymized, clustering results combined with other information might allow for re-identification of individuals within specific groups, especially for unique or outlier clusters. Techniques like differential privacy can be applied to clustering algorithms to provide mathematical guarantees about the privacy impact on individuals, but often come at the cost of reduced utility or accuracy.
Organizations must consider the privacy implications of their clustering activities and implement appropriate safeguards, including data minimization, anonymization techniques, and adherence to privacy regulations.
Regulatory Compliance (GDPR, CCPA)
Data privacy regulations like the General Data Protection Regulation (GDPR) in Europe and the California Consumer Privacy Act (CCPA) impose strict requirements on how personal data is collected, processed, and used. These regulations often apply to clustering activities when personal data is involved.
Key aspects include obtaining valid consent (if required), ensuring data minimization (collecting only necessary data), providing transparency about data processing activities (including profiling through clustering), and respecting individuals' rights (like the right to access, rectification, or erasure). Organizations need to ensure their clustering practices comply with applicable legal frameworks, which may require conducting data protection impact assessments and implementing privacy-preserving techniques.
Failure to comply can result in significant fines and reputational damage. Legal and compliance expertise is often needed to navigate the complexities of applying these regulations to machine learning practices like clustering.
Mitigation Strategies: Fairness-Aware Algorithms
Addressing bias and fairness concerns in clustering is an active research area. Several strategies are being explored. Pre-processing techniques aim to transform the data or feature space to remove bias before clustering. In-processing methods modify the clustering algorithm itself to incorporate fairness constraints during the cluster formation process.
Post-processing techniques adjust the cluster assignments after an initial clustering run to satisfy fairness criteria. Defining appropriate fairness metrics for unsupervised learning remains a challenge, as there are no predefined "correct" labels to compare against. Common approaches try to ensure demographic parity (equal representation across groups in clusters) or group-unaware fairness (similarity measures don't implicitly rely on sensitive attributes).
Implementing these fairness-aware techniques requires careful consideration of the specific fairness goals, potential trade-offs with accuracy or utility, and the ethical implications of different fairness definitions.
Future Trends in Clustering Technologies
Integration with Deep Learning
A significant trend is the integration of clustering with deep learning techniques. Deep learning models, particularly autoencoders, can learn complex, hierarchical representations (embeddings) of data. Applying clustering algorithms to these learned embeddings rather than the raw data often leads to better performance, especially for high-dimensional data like images or text.
Methods like Deep Embedded Clustering (DEC) jointly optimize the deep representation learning and the clustering objective. This allows the model to learn representations that are particularly well-suited for clustering. This synergy holds promise for uncovering intricate patterns in complex datasets where traditional clustering methods struggle.
Automated Hyperparameter Tuning
The sensitivity of many clustering algorithms to hyperparameters (like k in K-means or epsilon/MinPts in DBSCAN) is a practical challenge. Manually tuning these parameters can be time-consuming and requires expertise. Automated Machine Learning (AutoML) techniques, including automated hyperparameter optimization (HPO), are increasingly being applied to clustering.
Methods like Bayesian optimization, evolutionary algorithms, or reinforcement learning can automatically search for optimal hyperparameter configurations based on internal validation metrics. Meta-learning approaches aim to learn from past clustering tasks to predict good hyperparameters for new datasets more efficiently. This automation can make clustering more accessible and improve the consistency of results.
Quantum Computing Applications
Quantum computing holds potential, albeit still largely theoretical for practical applications, to accelerate certain types of computations relevant to clustering. Quantum algorithms have been proposed that could potentially offer speedups for tasks like finding nearest neighbors or solving optimization problems underlying some clustering formulations.
For instance, quantum algorithms might accelerate K-means or GMM optimization. Research is ongoing to develop and refine quantum clustering algorithms and understand their potential advantages and limitations compared to classical methods, especially as quantum hardware matures. This remains a forward-looking area with significant research challenges.
Edge Computing for Real-Time Clustering
With the proliferation of IoT devices and sensors generating vast amounts of data at the network edge, there's growing interest in performing clustering directly on these devices (edge computing) or close to them. This avoids the need to transmit large volumes of raw data to a central server, reducing latency, bandwidth consumption, and privacy concerns.
Edge clustering enables real-time pattern detection and anomaly identification directly where data is generated, supporting applications like real-time monitoring in industrial settings, autonomous vehicles, or smart cities. This requires developing lightweight, resource-efficient clustering algorithms suitable for deployment on devices with limited computational power and memory.
Challenges include algorithm adaptation, distributed coordination (if multiple edge devices collaborate), and managing model updates.
Frequently Asked Questions (Career Focus)
What prerequisites are needed for clustering roles?
Foundational prerequisites typically include a solid understanding of mathematics (Linear Algebra, Calculus, Probability, Statistics), proficiency in a programming language commonly used in data science (Python or R), and familiarity with core data manipulation and analysis libraries (e.g., Pandas, NumPy, scikit-learn).
Beyond the basics, a strong grasp of different clustering algorithms (K-means, Hierarchical, DBSCAN, GMMs), their strengths, weaknesses, and appropriate use cases is essential. Understanding distance metrics, dimensionality reduction techniques (like PCA), and cluster validation methods is also crucial.
For more advanced roles, experience with applying clustering to real-world problems, familiarity with big data tools (like Spark), and potentially knowledge of deep learning techniques for representation learning can be highly beneficial. Strong analytical and problem-solving skills are universally required.
Which industries hire the most clustering experts?
Expertise in clustering is valuable across many industries. Technology companies (including software, internet services, social media) heavily utilize clustering for user segmentation, recommendation systems, anomaly detection, and organizing information.
The Finance sector employs clustering for risk management, fraud detection, customer segmentation, and algorithmic trading strategies. Retail and E-commerce rely on it for customer analytics, market basket analysis, and personalized recommendations. Healthcare and Bioinformatics use clustering extensively for patient stratification, genomic analysis, and medical image segmentation.
Consulting firms also hire clustering experts to serve clients across various sectors. Essentially, any industry dealing with large amounts of data where discovering hidden groups or patterns provides value is likely to need clustering expertise.
How does clustering skill impact salary benchmarks?
Clustering is typically considered a core skill within the broader domains of Data Science and Machine Learning, rather than a standalone job title determining salary. Therefore, its impact on salary is intertwined with overall proficiency in data analysis, modeling, programming, and domain expertise.
Strong skills in unsupervised learning, including clustering, contribute significantly to the value a Data Scientist or Machine Learning Engineer brings. Deeper expertise, such as developing novel clustering methods or applying them effectively to complex, high-impact problems, can command higher salaries, particularly in specialized roles like Research Scientist or senior technical positions. According to the U.S. Bureau of Labor Statistics, data science roles generally offer competitive salaries, reflecting the demand for these analytical skills.
Ultimately, salary depends on factors like overall experience, education level, specific role responsibilities, industry, location, and the demonstrated impact of one's work.
Is remote work feasible in clustering-focused positions?
Yes, remote work is highly feasible for many roles involving clustering. The tasks involved – data analysis, algorithm implementation, model evaluation, programming – can typically be performed effectively from any location with a suitable internet connection and access to necessary computational resources (often cloud-based).
Many technology companies and data-driven organizations have embraced remote or hybrid work models for their data science and machine learning teams. Collaboration can be managed through virtual meetings, shared code repositories, and project management tools. Factors influencing remote feasibility include company culture, team structure, and the specific requirements of the role (e.g., need for access to specialized hardware or secure data environments).
Job postings often specify whether a position is remote, hybrid, or requires being on-site, allowing candidates to find opportunities matching their preferences.
What's the demand outlook compared to supervised learning?
Both supervised and unsupervised learning (including clustering) are critical components of modern machine learning and data science. Historically, supervised learning (like classification and regression) has seen wider direct application in many business contexts due to the prevalence of labeled data and clear prediction tasks.
However, the vast majority of the world's data is unlabeled, making unsupervised learning techniques like clustering increasingly important for extracting insights, discovering structure, and enabling downstream tasks. Clustering is fundamental for exploratory analysis, anomaly detection, and as a preprocessing step for supervised methods (e.g., generating features or segmenting data).
The demand is strong for professionals skilled in both paradigms. While supervised learning might appear in more job descriptions explicitly, a deep understanding of clustering and other unsupervised methods is often an expected or highly valued skill for comprehensive Data Scientist and Machine Learning Engineer roles. Demand for both areas is expected to remain robust as organizations continue to leverage data.
These foundational texts cover both supervised and unsupervised learning:
Can clustering skills support entrepreneurial ventures?
Absolutely. Clustering skills can be foundational for various entrepreneurial ventures. Identifying unmet needs or niche markets through customer segmentation is a direct application. Building products or services around automated data organization, anomaly detection, or personalized recommendations often relies heavily on clustering algorithms.
For example, a startup could develop a specialized tool for clustering scientific literature, a platform for detecting fraud in a specific industry using novel clustering techniques, or a consultancy focused on providing customer segmentation insights for small businesses. The ability to extract meaningful patterns from unlabeled data can uncover unique business opportunities.
Success requires not only technical expertise in clustering but also business acumen, market understanding, and the ability to translate technical capabilities into valuable products or services.
This book connects data science techniques like clustering to business value:
Clustering is a powerful and versatile set of techniques for uncovering hidden structures in data. From segmenting customers to grouping genes, its applications span numerous fields. While mastering clustering involves understanding mathematical concepts, various algorithms, and practical challenges, the journey offers rewarding opportunities for discovery and innovation. Whether pursuing formal education or leveraging online resources, developing expertise in clustering is a valuable asset in today's data-driven world, opening doors to exciting careers and the potential to make significant contributions.