Combinational Circuits

vigating the World of Combinational Circuits: A Comprehensive Guide Combinational circuits are a fundamental concept in digital electronics. At a high level, these circuits process input signals based on logical operations to produce output signals. Think of them as intricate decision-making networks where the output at any given moment is solely determined by the inputs at that exact same moment. This characteristic distinguishes them from other types of digital circuits and makes them essential for a wide array of applications. Working with combinational circuits can be quite engaging. Imagine designing the very logic that powers the calculator on your phone, enabling it to perform arithmetic operations almost instantaneously. Or consider the satisfaction of developing circuits that ensure the smooth transmission of data in communication systems or the reliable operation of industrial control systems. The ability to translate abstract logical concepts into tangible, functioning electronic systems is a core appeal for many who delve into this field. Furthermore, the ever-evolving landscape of technology means that combinational circuits are constantly finding new and exciting applications, such as in the development of specialized hardware for artificial intelligence.

Introduction to Combinational Circuits

To truly understand combinational circuits, it's important to grasp their basic principles and how they differ from their counterparts, sequential circuits. We'll also touch upon their historical context and some common places you might encounter them in your daily life.

Definition and Basic Principles of Combinational Circuits

A combinational circuit is a type of digital circuit where the output is exclusively dependent on the present input values. This means that the circuit has no memory of past inputs; it simply takes the current combination of '0s' and '1s' at its input terminals and, based on its internal logical structure, produces a corresponding set of '0s' and '1s' at its output terminals. These circuits are constructed using basic logic gates such as AND, OR, NOT, XOR, and others. Each gate performs a specific Boolean logic function. By interconnecting these gates in various configurations, more complex logical operations can be achieved. The behavior of a combinational circuit can be precisely described in a few ways. One common method is using Boolean algebra, which provides mathematical expressions that define the relationship between inputs and outputs. Another method is a truth table, which systematically lists all possible input combinations and their corresponding output values. These tools are fundamental to the design and analysis of combinational circuits. The key characteristic is that for any specific set of inputs, the output will always be the same, regardless of any previous inputs or outputs. This "memoryless" property is what defines them. They are designed to produce an output almost instantaneously in response to changes in input values.

Key Differences from Sequential Circuits

The primary distinction between combinational circuits and sequential circuits lies in the concept of memory. As we've established, combinational circuits are memoryless; their output is solely a function of their current inputs. In contrast, sequential circuits possess memory elements (like flip-flops or latches). This means the output of a sequential circuit depends not only on the current inputs but also on the past history of inputs, which is stored as the circuit's "state." Think of it this way: a simple calculator uses combinational circuits for arithmetic operations – the sum of 2 + 2 is always 4, regardless of what you calculated before. A digital counter, however, is a sequential circuit; to know the next number, it needs to remember the current number. Because of this memory aspect, sequential circuits often rely on clock signals to synchronize changes in their states, making them time-dependent. Combinational circuits, being independent of past states, do not typically require clock signals for their fundamental operation and can operate continuously as long as inputs are provided. This generally allows combinational circuits to operate faster than sequential circuits. This fundamental difference in how they handle information dictates their respective applications. Combinational circuits excel at tasks requiring immediate data processing and logical decision-making based on current conditions. Sequential circuits are essential for operations that require storing information, counting, or sequencing through states.

Historical Context and Foundational Inventors/Theories

The theoretical underpinnings of combinational circuits, and indeed all of digital logic, lie in Boolean algebra, developed by George Boole in the mid-19th century. His work provided a mathematical system for logical propositions, which later proved to be perfectly suited for describing the behavior of switching circuits. In the early to mid-20th century, Claude Shannon, in his master's thesis, famously demonstrated how Boolean algebra could be applied to analyze and design relay and switching circuits. This insight was a pivotal moment, laying the groundwork for modern digital circuit design. While it's difficult to pinpoint specific "inventors" of combinational circuits as a distinct category, the evolution of digital electronics saw numerous engineers and scientists contributing to the development and refinement of logic gates and their application in building complex systems. The progression from electromechanical relays to vacuum tubes, then to transistors, and finally to integrated circuits (ICs) allowed for increasingly complex and compact combinational (and sequential) logic to be realized. The development of systematic design methodologies, such as the use of truth tables and minimization techniques like Karnaugh maps (developed by Maurice Karnaugh in the 1950s), further streamlined the process of creating efficient combinational circuits. These theoretical and practical advancements collectively enabled the digital revolution.

Common Applications in Everyday Technology

Combinational circuits are ubiquitous in modern technology, often working silently behind the scenes in devices we use every day. One of the most straightforward examples is in calculators, where they perform arithmetic operations like addition, subtraction, multiplication, and division. The circuits that add two numbers or compare values are classic examples of combinational logic. In computers and microprocessors, combinational circuits are fundamental components of the Arithmetic Logic Unit (ALU), which handles all arithmetic and logical computations. They are also used in data routing, such as in multiplexers (which select one of many input signals to pass to a single output) and decoders (which convert a binary code into a specific output signal). For instance, a decoder might be used to select a particular memory location or to convert a binary number into a format that can be displayed on a seven-segment display (like those on older digital clocks or appliances). Consumer electronics are filled with combinational circuits. Think about digital clocks, remote controls, and even the display drivers in your television or smartphone. They are also crucial in communication systems for tasks like error detection and correction, ensuring data integrity during transmission. In industrial settings, combinational circuits are found in control systems that monitor processes and make decisions based on sensor inputs. Even a seemingly simple device like a digital thermometer uses combinational logic to convert sensor input into a readable temperature display. These examples only scratch the surface, but they illustrate the pervasive and essential role of combinational circuits in the technology that shapes our modern world.

Core Components and Boolean Logic

At the heart of every combinational circuit are fundamental building blocks and mathematical principles. Understanding logic gates and Boolean algebra is crucial for anyone looking to design or analyze these circuits. We'll also explore tools like truth tables and Karnaugh maps, which aid in visualizing and simplifying circuit logic.

Role of Logic Gates (AND, OR, NOT, XOR, etc.)

Logic gates are the elementary building blocks of digital circuits, including combinational circuits. Each gate performs a basic logical operation on one or more binary inputs (signals that are either a '0' or a '1', representing low or high voltage) to produce a single binary output. The most common logic gates include: * AND gate: The output is '1' only if all its inputs are '1'. Otherwise, the output is '0'. Think of it as requiring multiple conditions to be true simultaneously. * OR gate: The output is '1' if at least one of its inputs is '1'. The output is '0' only if all inputs are '0'. This represents a scenario where any one of several conditions being true is sufficient. * NOT gate (Inverter): This gate has only one input. The output is the opposite of the input. If the input is '1', the output is '0', and if the input is '0', the output is '1'. It essentially inverts the signal. * XOR (Exclusive OR) gate: The output is '1' if the inputs are different (one is '0' and the other is '1'). If both inputs are the same (both '0' or both '1'), the output is '0'. This is useful for tasks like checking for inequality or implementing binary addition. * NAND gate (NOT AND): This gate is equivalent to an AND gate followed by a NOT gate. The output is '0' only if all its inputs are '1'. Otherwise, the output is '1'. * NOR gate (NOT OR): This gate is equivalent to an OR gate followed by a NOT gate. The output is '1' only if all its inputs are '0'. Otherwise, the output is '0'. NAND and NOR gates are particularly interesting because they are considered "universal" gates. This means that any other logic gate (AND, OR, NOT, XOR) can be constructed using only NAND gates or only NOR gates. This property is often exploited in circuit design for simplification and standardization. By connecting these basic logic gates in various combinations, engineers can create circuits that perform complex logical functions, forming the basis of all combinational logic.

Boolean Algebra Principles

Boolean algebra is the mathematical system used to analyze and simplify digital logic circuits. It deals with binary variables (which can have only two values, typically 0 and 1) and logical operations. The fundamental operations in Boolean algebra correspond directly to the functions of logic gates: * AND operation: Represented by a dot (·) or sometimes by no symbol (e.g., A·B or AB). * OR operation: Represented by a plus sign (+) (e.g., A + B). * NOT operation: Represented by an overbar (Ā), a prime symbol (A'), or a tilde (~) (e.g., Ā or A'). Boolean algebra has a set of laws and theorems that allow for the manipulation and simplification of logical expressions. Some of the key principles include: * Commutative Laws: A + B = B + A; A · B = B · A * Associative Laws: (A + B) + C = A + (B + C); (A · B) · C = A · (B · C) * Distributive Laws: A · (B + C) = (A · B) + (A · C); A + (B · C) = (A + B) · (A + C) * Identity Laws: A + 0 = A; A · 1 = A * Complement Laws: A + Ā = 1; A · Ā = 0 * De Morgan's Theorems: These are particularly powerful for circuit simplification and converting between AND/OR logic and NAND/NOR logic. They state: * (A + B)' = A' · B' (The complement of a sum is the product of the complements) * (A · B)' = A' + B' (The complement of a product is the sum of the complements) By applying these algebraic rules, complex Boolean expressions representing a combinational circuit can often be reduced to simpler, equivalent expressions. A simpler expression usually translates to a circuit with fewer gates or fewer inputs to gates, which can lead to lower cost, reduced power consumption, and faster operation.

These books offer in-depth exploration of Boolean algebra and its application in digital design.

Truth Tables and Karnaugh Maps

While Boolean algebra provides a symbolic way to represent logic, **truth tables** offer a tabular method. A truth table lists all possible combinations of input values and the corresponding output value(s) for each combination. For a circuit with 'n' inputs, there will be 2ⁿ possible input combinations (rows in the truth table). This provides an exhaustive and unambiguous definition of a combinational circuit's behavior. For example, a simple 2-input AND gate would have the following truth table: | A | B | Output | |---|---|--------| | 0 | 0 | 0 | | 0 | 1 | 0 | | 1 | 0 | 0 | | 1 | 1 | 1 | Truth tables are invaluable for understanding circuit function and for deriving Boolean expressions. However, for circuits with many inputs, truth tables can become very large and unwieldy. This is where **Karnaugh maps (K-maps)** come in. A K-map is a graphical method used for simplifying Boolean expressions. It's a visual representation of a truth table, arranged in a way that allows for easy identification of groups of '1s' (or '0s') that can be combined to simplify the logic. K-maps are most commonly used for functions with two to five variables, as they become more complex to manage visually beyond that. The process involves plotting the output values from the truth table onto the K-map grid. Then, adjacent cells containing '1s' are grouped together in powers of two (e.g., groups of 1, 2, 4, 8). Each group represents a product term in the simplified Boolean expression. The goal is to cover all the '1s' on the map using the largest possible groups, with each '1' covered at least once. This graphical approach often makes it easier to spot simplification opportunities than purely algebraic manipulation, especially for moderately complex functions.

The following book provides a foundational understanding of these tools.

Circuit Minimization Techniques

The goal of circuit minimization is to reduce the complexity of a combinational circuit while preserving its logical function. A simpler circuit generally means fewer logic gates and interconnections, which can lead to several benefits: * **Lower cost:** Fewer components mean lower manufacturing costs. * **Reduced physical size:** A simpler circuit takes up less space on a printed circuit board or integrated circuit. * **Lower power consumption:** Fewer gates typically consume less power. * **Increased speed:** Signals may have shorter paths to travel, reducing propagation delays and allowing the circuit to operate faster. * **Improved reliability:** Fewer components and connections can sometimes lead to fewer potential points of failure. Several techniques are used for circuit minimization: 1. **Boolean Algebra:** As discussed earlier, applying the laws and theorems of Boolean algebra can simplify logical expressions. This often involves techniques like factoring, expanding terms, and applying De Morgan's theorems. 2. **Karnaugh Maps (K-maps):** This graphical method is very effective for functions with a small number of variables (typically up to 5 or 6). It allows for visual identification of redundant terms and simplification by grouping adjacent cells representing '1s' (for Sum-of-Products form) or '0s' (for Product-of-Sums form). 3. **Quine-McCluskey Algorithm:** For functions with a larger number of variables where K-maps become impractical, the Quine-McCluskey algorithm provides a tabular, systematic method for finding all prime implicants (terms that cannot be simplified further) and then selecting a minimal set of these prime implicants to cover the function. This method is more algorithmic and can be implemented by computer programs. 4. **Heuristic Methods:** For very complex circuits, exact minimization algorithms can be computationally intensive. Heuristic methods aim to find a "good" simplification, though not necessarily the absolute mathematical minimum, in a more reasonable amount of time. These are often used in modern computer-aided design (CAD) tools. Gate-level minimization specifically focuses on optimizing the arrangement and types of logic gates to achieve the desired function with the fewest resources. This might involve replacing a complex arrangement of AND, OR, and NOT gates with an equivalent circuit using fewer NAND or NOR gates, for example.

Understanding these minimization techniques is crucial for efficient digital design. This course delves into some of these methods.

Design Methodologies

Designing combinational circuits involves a systematic approach, moving from an abstract problem statement to a concrete hardware implementation. This process often leverages specialized software tools and includes considerations for ensuring the circuit operates correctly and reliably.

Step-by-Step Design Process

The design of a combinational circuit typically follows a structured procedure to ensure correctness and efficiency. While variations exist, a general step-by-step process includes: 1. Problem Specification and Understanding: The first and most crucial step is to clearly define what the circuit is supposed to do. This involves understanding the desired relationship between the inputs and outputs. Identify the number of input variables and the number of output variables required. It's often helpful to assign symbolic names to these inputs and outputs. 2. Truth Table Derivation: Based on the problem specification, construct a truth table. This table will list all possible combinations of input values and the corresponding required output values for each combination. This step formalizes the circuit's behavior. 3. Boolean Expression Derivation: From the truth table, derive the Boolean algebraic expressions for each output. This can be done by writing a sum-of-products (SOP) expression (summing all product terms for which the output is '1') or a product-of-sums (POS) expression (multiplying all sum terms for which the output is '0'). 4. Simplification of Boolean Expressions: Simplify the derived Boolean expressions using techniques like Boolean algebra laws, Karnaugh maps (K-maps), or the Quine-McCluskey algorithm. The goal is to obtain the simplest possible expressions, which usually lead to a more efficient circuit implementation. 5. Logic Diagram Implementation: Translate the simplified Boolean expressions into a logic diagram using standard logic gate symbols (AND, OR, NOT, XOR, etc.). This diagram provides a visual representation of the circuit's structure. 6. Verification and Testing: Verify that the designed circuit meets the original specifications. This can be done by manually analyzing the logic diagram, simulating the circuit using software tools, or building and testing a physical prototype. Test cases should cover various input combinations to ensure correct functionality. This iterative process ensures that the final circuit accurately implements the desired logic in an optimized manner.

These courses offer practical insights into the digital design process.

Software Tools for Circuit Simulation

Modern digital circuit design relies heavily on software tools, often referred to as Electronic Design Automation (EDA) or Computer-Aided Design (CAD) tools. These tools assist engineers at various stages of the design process, from schematic capture and simulation to synthesis and verification. 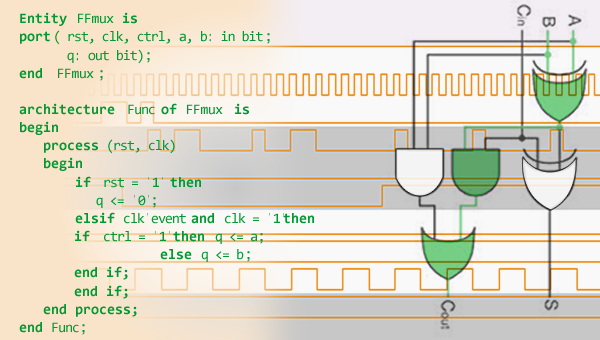For combinational circuit design and analysis, some key functionalities provided by these tools include: 1. Schematic Capture: Allows designers to draw logic diagrams graphically by selecting and connecting logic gate symbols from a library. 2. Hardware Description Languages (HDLs): Languages like VHDL (VHSIC Hardware Description Language) and Verilog allow designers to describe the behavior or structure of a digital circuit using text-based code. This is particularly useful for complex designs. 3. Logic Simulation: This is a critical function. Simulators take the schematic or HDL description of a circuit and apply input stimuli (sequences of '0s' and '1s') to predict the circuit's output behavior over time. This allows designers to verify the logical correctness of their design before physical implementation, saving time and resources. Simulators can display outputs as waveforms or truth tables. 4. Logic Synthesis: Synthesis tools can automatically convert an HDL description into a gate-level netlist (a description of the logic gates and their interconnections). These tools often incorporate optimization algorithms to minimize the circuit based on specified constraints (e.g., speed, area, power). 5. Timing Analysis: These tools analyze the propagation delays through the various paths in the circuit to ensure it meets timing requirements and to identify potential timing violations or race conditions. 6. Formal Verification: For critical applications, formal verification tools use mathematical methods to prove that a design meets its specification, offering a higher level of confidence than simulation alone. Examples of popular software tools used in both academic and professional settings include Logisim (an open-source graphical tool for learning), Xilinx Vivado/ISE, Intel Quartus Prime (often used for FPGA development), ModelSim (a popular simulator), and various tools from EDA vendors like Cadence, Synopsys, and Mentor Graphics (now Siemens EDA).

This course introduces VHDL programming using a popular industry tool.

If you're interested in Verilog, another widely used HDL, this course might be a good starting point.

Error Detection and Correction Methods

In digital systems, data can be corrupted during transmission or storage due to noise or hardware malfunctions. Combinational circuits play a vital role in implementing error detection and correction codes to ensure data integrity. Error Detection Codes: These codes add redundant bits to the original data to detect if an error has occurred. The receiver can check these bits to see if the data is likely correct. If an error is detected, the receiver might request a retransmission of the data. Common error detection schemes include: * Parity Check: This is the simplest error detection method. A single parity bit is added to a block of data. For *even parity*, the parity bit is set to '0' or '1' to make the total number of '1's in the data (including the parity bit) even. For *odd parity*, the total number of '1's is made odd. A combinational circuit (typically using XOR gates) can generate the parity bit at the sender's end and check it at the receiver's end. A single parity bit can detect any single-bit error but cannot detect all multi-bit errors (e.g., if two bits flip, the parity might still appear correct) and cannot correct any errors. * Checksum: A checksum is calculated based on the data bits (e.g., by summing them up and taking a complement). This checksum is transmitted with the data. The receiver recalculates the checksum from the received data and compares it with the received checksum. If they don't match, an error is detected. * Cyclic Redundancy Check (CRC): CRC is a more robust error detection method commonly used in data networks and storage devices. It involves polynomial division of the data by a predetermined generator polynomial. The remainder of this division is the CRC code, which is appended to the data. Combinational circuits (and sequential circuits for the division process) are used to implement CRC generation and checking. Error Correction Codes (ECC): These codes are more sophisticated as they can not only detect errors but also correct a certain number of them without requiring retransmission. They add more redundant bits than simple error detection codes. * Hamming Codes: Hamming codes are a well-known class of linear error-correcting codes. They can detect up to two-bit errors or correct single-bit errors. The placement of parity bits in Hamming codes is strategic, allowing the receiver to identify the position of a single-bit error. Combinational logic is used to calculate the parity bits and to determine the error location. * Reed-Solomon Codes: These are powerful error-correcting codes used in applications like CDs, DVDs, Blu-ray discs, data storage (RAID systems), and digital communications. They are particularly good at correcting burst errors (multiple consecutive bit errors). The design of circuits for error detection and correction involves careful application of Boolean logic to implement the encoding (adding redundant bits) and decoding (checking and correcting errors) processes.

Case Study: Designing a 4-bit Adder

Let's walk through a simplified design of a 4-bit binary adder, a common combinational circuit. A 4-bit adder takes two 4-bit binary numbers (say A = A3 A2 A1 A0 and B = B3 B2 B1 B0) and a carry-in (Cin) from a previous stage (if any) and produces a 4-bit sum (S = S3 S2 S1 S0) and a final carry-out (Cout). The fundamental building block for an adder is the **full adder**. A full adder is a combinational circuit that adds three single bits: two input bits (A and B) and a carry-in bit (Cin). It produces two outputs: a sum bit (S) and a carry-out bit (Cout). The truth table for a full adder is: | A | B | Cin | S | Cout | |---|---|-----|---|------| | 0 | 0 | 0 | 0 | 0 | | 0 | 0 | 1 | 1 | 0 | | 0 | 1 | 0 | 1 | 0 | | 0 | 1 | 1 | 0 | 1 | | 1 | 0 | 0 | 1 | 0 | | 1 | 0 | 1 | 0 | 1 | | 1 | 1 | 0 | 0 | 1 | | 1 | 1 | 1 | 1 | 1 | From this truth table, the Boolean expressions for S and Cout can be derived and simplified: S = A ⊕ B ⊕ Cin (where ⊕ denotes XOR) Cout = (A ⋅ B) + (Cin ⋅ (A ⊕ B)) or equivalently Cout = (A ⋅ B) + (A ⋅ Cin) + (B ⋅ Cin) To design a 4-bit adder, we can cascade four full adders. This is often called a **ripple-carry adder**. * The first full adder (FA0) takes A0, B0, and the initial Cin as inputs. It produces S0 and C_out0. * The second full adder (FA1) takes A1, B1, and C_out0 (the carry-out from FA0) as its carry-in. It produces S1 and C_out1. * The third full adder (FA2) takes A2, B2, and C_out1 as its carry-in. It produces S2 and C_out2. * The fourth full adder (FA3) takes A3, B3, and C_out2 as its carry-in. It produces S3 and the final Cout of the 4-bit adder. Visually, the carry "ripples" from one full adder to the next. While simple to design, the ripple-carry adder can be slow for many bits because the calculation of the most significant bits depends on the carry propagating through all the previous stages. More advanced adder designs, like the carry-lookahead adder, use more complex combinational logic to calculate carries faster, reducing the overall delay. This case study demonstrates how simpler combinational building blocks (full adders) can be combined to create more complex functional units.

Applications in Digital Systems

Combinational circuits are the workhorses of digital systems, performing essential tasks in a wide range of devices and technologies. From the core of computers to everyday gadgets and industrial machinery, their ability to perform logical operations and process data instantaneously makes them indispensable.

Use in Microprocessors and Memory Units

Microprocessors, the brains of computers and many electronic devices, heavily rely on combinational circuits. The Arithmetic Logic Unit (ALU) is a critical component of a microprocessor, responsible for performing arithmetic operations (like addition, subtraction) and logical operations (like AND, OR, NOT, XOR). The ALU itself is largely composed of combinational circuits, including adders, subtractors, comparators (which compare two binary numbers), and shifters (which shift bits left or right, used for multiplication/division by powers of two). Decoders are another vital combinational circuit used in microprocessors. For example, instruction decoders interpret the binary opcodes (operation codes) of machine language instructions, signaling the appropriate control units to execute the specified operation. Address decoders are used to select specific memory locations or I/O devices based on the address provided by the CPU. While memory units themselves (like RAM) inherently involve sequential circuits to store data, combinational circuits play supporting roles. For instance, multiplexers can be used to select data from different memory banks, and decoders are essential for selecting specific rows or columns of memory cells based on an address. Control logic within memory systems, which manages read and write operations, also utilizes combinational circuits to generate control signals.

This book provides an in-depth look at digital design, which is fundamental to understanding microprocessors.

Role in Consumer Electronics

Combinational circuits are pervasive in the consumer electronics we use daily. Calculators, for instance, are a classic example where combinational logic performs arithmetic calculations based on user input. Digital clocks, while also using sequential circuits for counting time, employ combinational circuits for tasks like decoding the time into a format suitable for display (e.g., driving seven-segment displays). Remote controls for televisions and other appliances use combinational logic to encode button presses into signals that can be transmitted. Within the television or appliance itself, decoders interpret these signals to perform the corresponding actions. Display drivers in screens (TVs, smartphones, monitors) utilize combinational circuits to process image data and control individual pixels. Even simpler devices often contain combinational logic. For example, a digital thermometer uses combinational circuits to convert the raw sensor reading into a temperature value and then to display that value. Digital cameras employ them for various data processing and control tasks. Essentially, any consumer electronic device that involves processing digital inputs to produce specific outputs or control actions will likely incorporate combinational circuits.

Industrial Automation and Control Systems

In the realm of industrial automation and control systems, combinational circuits are crucial for making real-time decisions based on sensor inputs and predefined logic. They are used to implement control logic for machinery, monitor industrial processes, and ensure safety protocols are followed. For example, a combinational circuit might take inputs from various sensors on a production line (e.g., proximity sensors, temperature sensors, pressure sensors) and, based on a specific set of logical conditions, activate or deactivate actuators (e.g., motors, valves, alarms). Consider a safety interlock system where a machine will only operate if multiple safety guards are in place and an emergency stop button is not pressed; this logic can be implemented directly with combinational circuits. Programmable Logic Controllers (PLCs), which are widely used in industrial automation, often execute programs that implement combinational (and sequential) logic to control complex processes. While the PLC itself is a microprocessor-based system, the underlying logical operations it performs are based on the principles of combinational circuits. They are used in applications ranging from simple machine control to complex process control in manufacturing plants, chemical processing, and power generation.

Emerging Applications in AI Hardware

As Artificial Intelligence (AI) and Machine Learning (ML) continue to advance, there's a growing demand for specialized hardware that can efficiently execute AI algorithms. Combinational circuits are playing an increasingly important role in the development of AI hardware accelerators. Many AI computations, particularly in deep learning models, involve massive numbers of matrix multiplications and activation function calculations. These operations can be implemented efficiently using dedicated combinational circuits. By designing custom hardware tailored for these specific tasks, AI accelerators (like GPUs, TPUs, and other ASICs) can achieve significantly higher performance and lower power consumption compared to general-purpose CPUs. For instance, circuits for high-speed parallel multiplication and addition are fundamental to accelerating neural network training and inference. Combinational logic is also used in designing the control units and data paths within these specialized AI chips. The integration of combinational circuits directly into AI hardware is a key strategy for pushing the boundaries of AI performance and enabling more complex AI applications across various fields, from autonomous vehicles to medical diagnostics.

For those interested in the broader field of digital circuits, which encompasses combinational logic, this is a relevant topic.

Formal Education Pathways

For individuals aspiring to work with combinational circuits, a strong foundation in digital electronics and related fields is typically acquired through formal education. This path often involves university degrees, specific coursework, and hands-on laboratory experience.

Relevant Undergraduate/Graduate Degrees

A bachelor's degree in Electrical Engineering (EE) or Computer Engineering (CpE) is the most common starting point for a career involving combinational circuit design. These programs provide a comprehensive understanding of electronic circuits, digital logic, computer architecture, and semiconductor devices. Some universities may offer specializations within these degrees that focus more specifically on digital systems, VLSI (Very Large Scale Integration) design, or embedded systems. Other related undergraduate degrees could include Electronics Engineering Technology, or even Computer Science (CS) with a strong hardware focus or a minor in electrical/computer engineering. While a CS degree might lean more towards software, understanding the underlying hardware, including combinational logic, is beneficial for systems-level programming and computer architecture roles. For those seeking more advanced roles in research, design of complex integrated circuits (ICs), or specialized areas like AI hardware acceleration, a Master's or Ph.D. degree in Electrical Engineering or Computer Engineering is often preferred or required. Graduate studies allow for deeper specialization in areas such as advanced digital design, VLSI design methodologies, computer architecture, low-power design, and emerging semiconductor technologies.

Key Courses (e.g., Digital Electronics, VLSI Design)

Within an EE or CpE curriculum, several courses are fundamental for understanding and working with combinational circuits: * Digital Logic Design / Digital Electronics: This is typically the foundational course. It introduces Boolean algebra, logic gates, combinational circuit analysis and design (adders, decoders, multiplexers, etc.), sequential circuits (flip-flops, counters, registers), and state machine design. * Computer Organization and Architecture: This course explores how digital logic components are used to build computer systems. It covers topics like instruction set architectures, CPU design, memory systems, and I/O organization, all of which involve combinational logic.

* Microelectronics / Semiconductor Devices: These courses delve into the physics and operation of transistors and other semiconductor devices, which are the physical basis for logic gates. * VLSI (Very Large Scale Integration) Design: This is a more advanced course focusing on the design and fabrication of integrated circuits (ICs or "chips"). It covers CMOS logic design, layout, timing, power considerations, and the use of EDA tools for designing complex digital systems, including those with extensive combinational logic. * Embedded Systems Design: This area involves designing computer systems for specific functions within larger mechanical or electrical systems. It often requires a deep understanding of hardware-software interaction, including the design of digital interfaces using combinational and sequential logic.

* Hardware Description Languages (HDLs): Courses or modules covering VHDL or Verilog teach students how to describe, simulate, and synthesize digital circuits using these industry-standard languages. These courses often build upon each other, providing a progressively deeper understanding of how combinational circuits are designed, implemented, and utilized in complex digital systems.

These courses provide a solid introduction to digital systems and computing fundamentals.

Laboratory Requirements and Research Opportunities

Hands-on experience is a critical component of learning about combinational circuits. University programs in electrical and computer engineering almost invariably include laboratory sessions that complement the theoretical coursework. These labs allow students to: * Build and Test Circuits: Students typically start by building simple combinational circuits on breadboards using discrete logic gate ICs. They learn to use lab equipment like power supplies, oscilloscopes, logic analyzers, and function generators to test and troubleshoot their designs. * Use Simulation Software: Labs introduce students to EDA tools for schematic capture and logic simulation. They learn to design circuits virtually, apply input stimuli, and analyze the output waveforms to verify functionality before (or instead of) physical implementation. * Work with FPGAs: Field-Programmable Gate Arrays (FPGAs) are integrated circuits that can be configured by the user after manufacturing. Many universities use FPGAs in advanced digital design labs. Students learn to describe their circuits using HDLs (like VHDL or Verilog), synthesize them onto the FPGA, and test their designs on actual hardware. This provides experience with a technology widely used in prototyping and even in some production systems. * Undertake Design Projects: Capstone design projects or other project-based courses often require students to design and implement more complex digital systems, which invariably involve significant combinational (and sequential) logic components. For students interested in pushing the boundaries of knowledge in this field, research opportunities may be available, especially at the graduate level. Faculty members often conduct research in areas like novel computer architectures, low-power digital design, reconfigurable computing, AI hardware, hardware security, and emerging semiconductor technologies. Participating in such research can provide invaluable experience and contribute to the advancement of the field.

PhD-Level Specializations

A Ph.D. in Electrical Engineering or Computer Engineering allows for deep specialization in areas related to combinational circuits and digital systems. These advanced studies typically involve rigorous coursework, comprehensive exams, and, most importantly, original research culminating in a doctoral dissertation. Some potential Ph.D.-level specializations include: * Advanced VLSI Design and Methodologies: Focusing on the design of highly complex integrated circuits, including system-on-chip (SoC) design, low-power and high-performance circuit techniques, advanced CAD tool development, and design for manufacturability/testability. * Computer Architecture: Researching novel processor architectures, memory hierarchies, parallel computing systems, and specialized architectures for specific applications (e.g., AI, bioinformatics, cryptography). This often involves designing and evaluating new hardware structures built from combinational and sequential logic. * Reconfigurable Computing: Exploring architectures and design tools for FPGAs and other reconfigurable hardware, aiming to create systems that can adapt their hardware structure to different tasks. * Hardware Security and Trust: Investigating methods to design secure hardware, protect against side-channel attacks, detect hardware Trojans, and ensure the integrity of integrated circuits throughout their lifecycle. * Emerging Computing Technologies: Researching beyond traditional CMOS technology, such as quantum computing (though the direct application of classical combinational circuit skills differs, the foundational understanding of logic is useful), neuromorphic computing (brain-inspired computing), or circuits based on new materials and devices. * AI Hardware Acceleration: Designing specialized hardware architectures to efficiently execute AI and machine learning algorithms, focusing on optimizing performance, power, and area for tasks like neural network training and inference. A Ph.D. typically prepares individuals for careers in academic research and teaching, or for advanced research and development roles in industry, particularly in semiconductor companies, high-tech firms, and research labs.

Self-Directed Learning Strategies

For those who prefer a more flexible approach or wish to supplement formal education, self-directed learning offers numerous avenues to understand and master combinational circuits. This path can be particularly appealing to curious learners and professionals looking to upskill.

Open-Source Simulation Tools (e.g., Logisim)

Several excellent open-source software tools are available that allow individuals to design, simulate, and experiment with digital logic circuits, including combinational circuits, without needing expensive commercial licenses or physical lab equipment. One of the most popular and user-friendly tools for educational purposes is Logisim. Logisim provides a graphical interface where users can drag and drop logic gates, wires, input/output pins, and other components to build circuits. It allows for real-time simulation, so you can flip input switches and immediately see the outputs change on LEDs or other indicators. It also supports building more complex circuits by creating sub-circuits, which is great for hierarchical design. Other open-source options might include tools like Icarus Verilog (a Verilog simulator) and GHDL (a VHDL simulator), which are more text-based (using Hardware Description Languages) and cater to those wanting to learn industry-standard HDLs. Using these tools, learners can: * Visualize how different logic gates function. * Build and test basic combinational circuits like adders, decoders, and multiplexers. * Experiment with Boolean algebra by implementing and simplifying expressions. * Gain an intuitive understanding of how digital signals propagate and how circuits behave. These tools provide a safe and accessible environment for trial-and-error learning, which is invaluable for grasping the practical aspects of combinational circuit design.

Project-Based Learning Ideas (e.g., Building Basic ALUs)

One of the most effective ways to solidify understanding in a technical field is through project-based learning. Instead of just reading about concepts, you apply them to build something tangible (even if it's a virtual circuit in a simulator). For combinational circuits, here are some project ideas, starting simple and increasing in complexity: 1. Design a 2-to-4 Line Decoder: Take two input lines and activate one of four output lines based on the binary input. 2. Build a 4-to-1 Multiplexer: Create a circuit that selects one of four data inputs to be routed to a single output, based on two select lines. 3. Implement a Half Adder and a Full Adder: Start with adding two single bits (half adder), then extend it to add three bits (full adder, including a carry-in). 4. Construct a 4-bit Ripple-Carry Adder: Cascade four full adders to create a circuit that can add two 4-bit binary numbers. 5. Design a Simple Magnitude Comparator: Create a circuit that takes two 2-bit numbers and determines if the first is greater than, less than, or equal to the second. 6. Build a Basic Arithmetic Logic Unit (ALU): This is a more ambitious project. An ALU is the core of a CPU that performs arithmetic and logical operations. A simple ALU might take two 2-bit or 4-bit numbers and an operation select input. Based on the select input, it could perform operations like ADD, SUBTRACT (using 2's complement), AND, and OR. This project integrates many smaller combinational circuit concepts. 7. BCD to 7-Segment Decoder: Design a circuit that takes a 4-bit Binary Coded Decimal (BCD) input (representing digits 0-9) and outputs the 7 signals needed to display that digit on a common-cathode 7-segment display. Working on such projects, especially with simulation tools, allows you to see theory in action, debug problems, and gain a much deeper and more practical understanding of combinational circuit design.

Technical Communities and Forums for Support

Learning, especially self-directed learning, can sometimes be challenging. Encountering roadblocks or having questions is a natural part of the process. Fortunately, there are many online technical communities and forums where you can seek help, share your projects, and learn from others. Websites like Stack Exchange (specifically Electrical Engineering Stack Exchange or Computer Science Stack Exchange), Reddit (e.g., subreddits like r/electronics, r/ElectricalEngineering, r/ComputerEngineering, r/FPGA), and dedicated electronics or hobbyist forums can be invaluable resources. When asking questions, it's always a good idea to be specific, describe what you've already tried, and what you're trying to achieve. Many open-source tools also have their own user communities or mailing lists. Engaging with these communities can not only provide solutions to specific problems but also expose you to new ideas, different approaches to design, and interesting projects that others are working on. Sharing your own progress and helping others when you can also reinforces your own learning. Platforms like GitHub can be used to share your circuit design files or HDL code for projects, allowing for collaboration and feedback.

Certifications vs. Skill Portfolios

When it comes to demonstrating your knowledge and skills in combinational circuits, especially if you're self-taught or looking to enhance your resume, the question of certifications versus a skill portfolio often arises. **Certifications:** In the specific domain of fundamental combinational circuit design (as opposed to, say, FPGA vendor-specific certifications or broader electronics technician certifications), standalone certifications are less common. However, certifications related to specific HDLs (VHDL, Verilog) or proficiency with particular EDA tools might be available from software vendors or training institutions. While a certification can show that you've passed a certain level of assessment, its value can vary. Some employers might see it as a plus, while others might place more emphasis on demonstrable skills and experience. **Skill Portfolios:** A skill portfolio, on the other hand, is a collection of projects and work samples that directly showcase your abilities. For combinational circuits, this could include: * Schematic diagrams and simulation results of circuits you've designed (e.g., using Logisim). * HDL code (VHDL/Verilog) for more complex designs, perhaps with testbenches and synthesis reports if you've worked with FPGAs. * Detailed write-ups of your projects, explaining the design choices, challenges faced, and solutions implemented. * Contributions to open-source hardware projects. A well-curated portfolio provides tangible evidence of your skills and passion for the subject. It allows potential employers or collaborators to see what you can actually *do*, rather than just what you *know*. For many technical roles, especially in design, a strong portfolio can be more impactful than a list of certifications, particularly if those certifications aren't widely recognized or directly relevant to the job. Ultimately, a combination can be beneficial. If relevant and reputable certifications are available, they can complement a strong portfolio. However, if you have to choose where to focus your energy as a self-directed learner, building a robust portfolio of interesting and challenging projects is often the more compelling path to demonstrate your expertise in combinational circuit design.

OpenCourser offers a vast library of courses that can help you build foundational knowledge. You can browse engineering courses to find topics that align with your learning goals. The platform's features like summarized reviews and "Save to List" can help you identify and organize courses effectively.

Career Opportunities and Progression

A solid understanding of combinational circuits opens doors to a variety of career opportunities in the fields of digital electronics, computer engineering, and beyond. The skills developed are foundational for roles ranging from entry-level design positions to leadership in research and development.

Entry-Level Roles (e.g., Digital Design Engineer)

With a relevant bachelor's degree (typically in Electrical Engineering or Computer Engineering) and a good grasp of digital logic fundamentals, including combinational circuit design, individuals can pursue several entry-level roles: * Digital Design Engineer: This is a common entry point. Responsibilities might include designing, simulating, and verifying digital circuits (both combinational and sequential) using HDLs like Verilog or VHDL. They might work on components of larger systems, such as specific modules within an FPGA or an ASIC.

* Hardware Engineer: A broader role that can involve various aspects of hardware development, including digital circuit design, PCB (Printed Circuit Board) design, and system integration. * Test Engineer / Verification Engineer: These roles focus on ensuring that digital designs function correctly and meet specifications. This involves developing test plans, writing testbenches (often in HDLs), and using simulation and formal verification tools to find bugs in the design. While not purely design, a strong understanding of how circuits work is essential.

* Embedded Systems Engineer (entry-level): Designing and programming the hardware and firmware for embedded systems often requires knowledge of digital logic for interfacing with sensors, actuators, and other peripherals.

For those new to the field, it's encouraging to know that these foundational skills are always in demand. While breaking into any engineering field requires dedication and effort, the principles of combinational logic are timeless. Building a strong portfolio of projects, even academic ones or those done in a home lab, can significantly enhance your prospects. Be prepared for technical interviews that will likely probe your understanding of Boolean algebra, logic gates, and basic circuit design principles.

This book can be a valuable resource for aspiring digital designers.

Mid-Career Paths (FPGA Development, ASIC Design)

As professionals gain experience and expertise, they can move into more specialized and complex roles. Mid-career paths for those with a strong background in combinational circuits often involve: * FPGA Design Engineer: This role focuses on designing and implementing digital systems using Field-Programmable Gate Arrays. FPGAs offer flexibility as they can be reprogrammed, making them suitable for prototyping, custom computing applications, and products with evolving requirements. FPGA designers use HDLs extensively and work with sophisticated EDA tools for synthesis, place-and-route, and timing analysis.

* ASIC (Application-Specific Integrated Circuit) Design Engineer: ASICs are custom-designed chips optimized for a particular application, offering higher performance and lower power consumption compared to FPGAs for high-volume products. ASIC design is a complex process involving detailed front-end design (logic design using HDLs, simulation, verification) and often back-end design (physical layout, timing closure). This path requires deep expertise in digital design, semiconductor technology, and EDA tools. * Senior Digital Design Engineer: With experience, engineers take on more responsibility, leading design projects, mentoring junior engineers, and tackling more challenging design problems. They might specialize in areas like high-speed digital design, low-power design, or specific application domains. * System Architect / Computer Architect: These roles involve defining the high-level architecture of complex digital systems, including processors, SoCs (Systems-on-Chip), or specialized hardware. A profound understanding of how combinational and sequential logic elements are combined to build larger systems is crucial.

Transitioning into these roles typically requires several years of hands-on experience, a proven track record of successful projects, and continuous learning to keep up with evolving technologies and design methodologies. The path can be demanding, but it's also incredibly rewarding to be at the forefront of designing cutting-edge hardware.

Leadership Roles in R&D

For individuals with extensive experience, deep technical expertise, and often advanced degrees (Master's or Ph.D.), leadership roles in Research and Development (R&D) become attainable. These positions involve: * Principal Engineer / Staff Engineer: These are highly technical individual contributor roles where engineers are recognized experts in their field. They often tackle the most complex technical challenges, drive innovation, and set technical direction for projects or even entire product lines. * Engineering Manager / Director: These roles combine technical leadership with people management. Managers oversee teams of engineers, guide project execution, manage resources, and contribute to strategic planning. While they might do less hands-on design, a strong technical background is essential for effective leadership. * Chief Technology Officer (CTO) / VP of Engineering (in hardware-focused companies): At the executive level, these roles involve setting the overall technology vision and strategy for the company, overseeing all engineering activities, and making critical decisions about technology investments and R&D directions. * Research Scientist / Academic Professor: For those in academia or corporate research labs, leadership roles involve leading research groups, securing funding, publishing cutting-edge research, and mentoring the next generation of engineers and researchers in areas related to digital circuits, computer architecture, or semiconductor technology. Advancing to these leadership positions requires not only exceptional technical skills but also strong communication, problem-solving, strategic thinking, and leadership abilities. It's a journey that often involves decades of dedication to the field.

Transferable Skills to Adjacent Fields (Robotics, IoT)

The skills gained from mastering combinational circuits and digital design are highly transferable to several adjacent and rapidly growing fields: * Robotics: Robots rely heavily on embedded systems to control their sensors, actuators, and decision-making processes. Understanding digital logic is crucial for designing the interfaces between the robot's "brain" (often a microprocessor or microcontroller) and its physical components. * Internet of Things (IoT): IoT devices are essentially small, interconnected embedded systems. Designing the hardware for IoT devices, including sensor interfaces, communication modules, and low-power processing units, requires digital design skills.

* Digital Signal Processing (DSP): Many DSP algorithms are implemented in hardware for real-time performance (e.g., in audio/video processing, telecommunications). Designing DSP hardware involves creating custom data paths and control logic using combinational and sequential circuits.

* Automotive Electronics: Modern vehicles are packed with electronic control units (ECUs) that manage everything from the engine and transmission to safety systems and infotainment. Designing and verifying these automotive-grade digital circuits is a significant field. * Aerospace and Defense: These industries require highly reliable and often radiation-hardened digital electronics for communication, navigation, and control systems. * Medical Devices: From diagnostic equipment to implantable devices, medical electronics often require custom digital circuits with stringent safety and reliability requirements. The fundamental ability to think logically, break down complex problems, and design systems at the bit level is a valuable asset in any field that involves digital hardware. Even if your career path diverges from pure circuit design, the analytical skills honed by studying combinational circuits will remain relevant.

If you're exploring career options, OpenCourser's "Career Center" feature on course pages can provide insights into roles related to specific areas of study.

You might also find these related careers interesting:

Challenges and Ethical Considerations

While the design and application of combinational circuits drive technological advancement, engineers and researchers in this field also grapple with significant challenges and important ethical considerations. These range from physical limitations of the technology to broader societal impacts.

Power Consumption and Thermal Limitations

As digital circuits become more complex and densely packed onto integrated circuits (ICs), power consumption becomes a major concern. Each logic gate switching state consumes a small amount of power. In a circuit with millions or billions of transistors, this can add up to significant power draw. High power consumption not only impacts battery life in portable devices but also leads to increased energy costs for larger systems like data centers. A direct consequence of power consumption is heat generation. As circuits consume power, much of it is dissipated as heat. If this heat is not effectively managed, it can raise the temperature of the IC to levels that can cause performance degradation, intermittent errors, or even permanent damage. This is known as thermal limitation. Designing cooling solutions (heat sinks, fans, liquid cooling) adds to the cost and complexity of systems. Therefore, a significant challenge in modern digital design, including combinational circuits, is to achieve the desired functionality and performance while minimizing power consumption and managing thermal output. This involves techniques at all levels, from transistor design and logic gate optimization to architectural choices and power management strategies.

Security Vulnerabilities in Hardware Design

Historically, cybersecurity has focused primarily on software vulnerabilities. However, there's a growing recognition that hardware itself can be a source of security vulnerabilities. Combinational circuits, as fundamental building blocks of hardware, are not immune to these concerns. * Side-Channel Attacks: These attacks exploit physical characteristics of a circuit's operation, such as its power consumption, electromagnetic emissions, or timing variations, to infer secret information (like cryptographic keys). The way combinational logic is implemented can influence its susceptibility to such attacks. * Hardware Trojans: Malicious modifications to a circuit design, inserted during design or fabrication (often by an untrusted party in the supply chain), are known as hardware Trojans. These could be designed to cause malfunctions, leak sensitive information, or create a backdoor. Detecting these tiny, malicious additions within complex combinational logic is a significant challenge. * Fault Injection Attacks: Intentionally inducing faults (e.g., by manipulating voltage or clock signals) into a circuit can cause it to behave in unexpected ways, potentially bypassing security mechanisms or revealing sensitive data. The design of combinational logic can influence its resilience to such attacks. * Reverse Engineering and IP Theft: Malicious actors may attempt to reverse engineer an IC to understand its combinational logic and steal intellectual property (IP) or find vulnerabilities. Designing secure hardware requires considering these threats from the outset. This includes developing design techniques that are resistant to side-channel analysis, implementing robust verification methods to detect Trojans, and incorporating countermeasures against fault injection.

Environmental Impact of Semiconductor Manufacturing

The fabrication of semiconductor devices, which house combinational circuits, is a highly complex and resource-intensive process with significant environmental implications. * Energy Consumption: Semiconductor fabrication plants (fabs) consume vast amounts of electricity, much of which may come from fossil fuels, contributing to greenhouse gas emissions. * Water Usage: The manufacturing process requires enormous quantities of ultrapure water for cleaning and rinsing silicon wafers at various stages. This can strain local water resources, especially in water-scarce regions. * Chemical Waste: A wide array of hazardous chemicals, including solvents, acids, and specialty gases, are used in etching, deposition, and other manufacturing steps. Managing, treating, and disposing of these chemical wastes and byproducts is a critical environmental challenge to prevent air and water pollution. * Greenhouse Gas Emissions: Beyond energy consumption, some manufacturing processes directly release potent greenhouse gases (e.g., perfluorocarbons used in etching). * Resource Depletion: The extraction and processing of raw materials like silicon, rare earth elements, and various metals also have environmental footprints. The semiconductor industry is increasingly aware of these impacts and is exploring ways to make chip production more sustainable. This includes investing in renewable energy sources, improving energy and water efficiency, developing greener chemical processes, and enhancing waste management and recycling efforts. According to a 2020 research paper mentioned by Earth.Org, chip manufacturing accounts for a significant portion of the carbon footprint of electronic devices. Efforts to mitigate these impacts are crucial for balancing technological progress with environmental stewardship.

Ethical Implications of Automation

Combinational circuits are fundamental to automation, which spans from industrial robots to AI-driven decision-making systems. While automation brings numerous benefits like increased efficiency, productivity, and safety in some contexts, it also raises significant ethical questions: * Job Displacement: As automated systems become more capable, there are concerns about the displacement of human workers in various industries. While new jobs may be created in designing, maintaining, and managing these automated systems, there's a societal challenge in ensuring a just transition for affected workforces. * Bias in Algorithmic Decision-Making: If AI systems, which rely on underlying hardware (including combinational logic for acceleration), are trained on biased data or have flaws in their algorithms, they can perpetuate and even amplify societal biases in areas like hiring, loan applications, or criminal justice. * Accountability and Responsibility: When an autonomous system (e.g., a self-driving car or an automated weapon system) makes an error leading to harm, determining accountability can be complex. Is it the designer, the manufacturer, the owner, or the AI itself (if that's even a coherent concept)? * Surveillance and Privacy: The proliferation of smart devices and sensors, all built on digital electronics, enables unprecedented levels of data collection. This raises concerns about surveillance, privacy, and the potential for misuse of personal information. * Over-Reliance and Deskilling: As societies become more reliant on automated systems, there's a potential for human skills in certain areas to atrophy. There's also the risk associated with the failure of critical automated systems if backups or human oversight are inadequate. Engineers and designers of combinational circuits and the broader systems they enable have a role to play in considering these ethical dimensions. This includes designing for safety, security, and transparency, as well as participating in broader societal discussions about the responsible development and deployment of automation technologies.

Frequently Asked Questions (Career Focus)

For those considering a career path related to combinational circuits, several common questions often arise regarding educational requirements, job market competitiveness, skill transferability, and industry trends.

Is a computer engineering degree mandatory for this field?

While a Bachelor's degree in Computer Engineering (CpE) or Electrical Engineering (EE) is the most traditional and direct route into fields heavily involving combinational circuit design, it's not always an absolute ironclad requirement, though it is highly advantageous. Many employers in areas like digital design, FPGA development, and ASIC design will explicitly list a CpE or EE degree as a primary qualification. These programs provide the rigorous theoretical foundation in digital logic, circuit theory, semiconductor physics, and computer architecture that is essential for these roles. They also typically include crucial hands-on lab experience. However, individuals with degrees in related fields like Electronics Engineering Technology, or even Computer Science with a strong hardware concentration and demonstrable project experience, might find opportunities, especially in roles that are more focused on system integration, testing, or firmware development that interfaces closely with hardware. For those without a directly relevant degree, building an exceptionally strong portfolio of projects, possibly supplemented by online courses and certifications (though the latter are less standardized for core circuit design), becomes even more critical. It's about proving you have the necessary knowledge and skills. Some individuals might also transition from technician roles with significant experience and further self-study. The key is to demonstrate a deep understanding of the fundamental principles and practical application.

How competitive are entry-level positions?

The competitiveness of entry-level positions in fields related to combinational circuit design (like digital design engineer, hardware engineer) can vary depending on several factors, including the overall economic climate, the specific industry segment, and geographical location. Generally, engineering roles are competitive, and companies often seek candidates with strong academic records, relevant internship experience, and good problem-solving skills. For highly sought-after positions at top-tier technology companies, competition can be intense. However, the demand for skilled digital hardware engineers remains steady due to the continuous advancement of technology in areas like consumer electronics, telecommunications, automotive, AI hardware, and IoT. To enhance competitiveness, students should: * Strive for a strong GPA in relevant coursework. * Actively seek internships or co-op opportunities to gain practical experience. * Develop a portfolio of personal or academic projects that showcase design and problem-solving abilities. * Hone their understanding of fundamental concepts (Boolean algebra, logic gates, FSMs, computer architecture). * Practice for technical interviews, which often involve whiteboard problem-solving related to digital logic. * Network with professionals in the field. While it requires effort, those who are passionate about digital design and can demonstrate their capabilities have a good chance of securing rewarding entry-level positions.

Can combinational circuit skills transition to quantum computing?

The skills acquired in classical combinational circuit design have some conceptual overlap and can provide a helpful foundation, but a direct one-to-one transition to designing quantum circuits requires significant new learning. What transfers well: * **Logical Thinking and Problem Decomposition:** The ability to break down complex problems into smaller, manageable logical steps is valuable in both classical and quantum computing. * **Understanding of Gates and Circuits:** The concept of using gates to manipulate information and stringing them together to form circuits is analogous. Classical logic gates have quantum counterparts (quantum gates). * **Algorithmic Thinking:** While quantum algorithms differ significantly, a strong foundation in classical algorithmic thinking is beneficial. * **Mathematical Aptitude:** Both fields require a good grasp of mathematics, though the specific branches differ (Boolean algebra for classical, linear algebra and probability for quantum). What needs to be learned: * **Quantum Mechanics:** A fundamental understanding of quantum mechanics, including concepts like qubits, superposition (where a qubit can be 0, 1, or a combination simultaneously), and entanglement (where qubits become interlinked), is essential. * **Linear Algebra:** Quantum states and operations are described using vectors and matrices. Proficiency in linear algebra is crucial. * **Probability Theory:** Measurement in quantum computing is probabilistic, so understanding probability is key. * **Quantum Gates and Algorithms:** One must learn about specific quantum gates (Hadamard, CNOT, Pauli gates, etc.) and how they are used to construct quantum circuits to implement quantum algorithms (e.g., Shor's algorithm, Grover's algorithm). * **Different Computational Model:** Quantum computing operates on fundamentally different principles than classical computing. It's not just about making classical circuits faster but leveraging quantum phenomena for new types of computation. So, while a background in combinational circuits provides a good starting point in terms of structured thinking about logic and circuits, transitioning to quantum computing necessitates a deep dive into quantum physics and advanced mathematics. It's more of a related but distinct field. Some sources suggest that a basic understanding of electronics can be helpful if one is interested in the hardware aspect of quantum computing.

If you're curious about this advanced field, OpenCourser has resources on Artificial Intelligence, which sometimes intersects with advanced computing paradigms.

What industries hire the most combinational circuit experts?

Experts in combinational circuits, more broadly digital design engineers and hardware engineers, are sought after in a variety of industries. Some of the most prominent include: 1. Semiconductor Industry: Companies that design and manufacture integrated circuits (CPUs, GPUs, FPGAs, ASICs, memory chips) are primary employers. This includes major players and smaller design houses. 2. Consumer Electronics: Manufacturers of smartphones, computers, televisions, gaming consoles, and other gadgets rely heavily on digital hardware design. 3. Telecommunications: Companies developing networking equipment, mobile communication infrastructure (like 5G base stations), and optical communication systems require digital design expertise for high-speed data processing and control. 4. Automotive: The automotive industry is increasingly reliant on electronics for engine control units (ECUs), advanced driver-assistance systems (ADAS), infotainment systems, and electric vehicle (EV) technology. 5. Aerospace and Defense: These sectors require highly reliable digital electronics for avionics, guidance systems, communication systems, and weaponry. 6. Industrial Automation and Control: Companies developing PLCs, robotics, and other industrial control systems use digital logic for process control and automation. 7. Computing and Data Centers: Designers of servers, storage systems, and high-performance computing (HPC) clusters need experts in digital hardware. 8. AI and Machine Learning Hardware: A rapidly growing sector involves designing specialized hardware accelerators (e.g., TPUs, custom ASICs) for AI and ML applications. 9. Medical Devices: Manufacturers of diagnostic equipment, patient monitoring systems, and implantable medical devices employ digital design engineers. 10. Research and Development: Universities and corporate research labs also hire experts to push the boundaries of digital circuit design and computer architecture. Essentially, any industry that involves the creation or use of sophisticated electronic devices and systems will have a need for individuals skilled in combinational logic and digital design.

How does AI affect job prospects in hardware design?

Artificial Intelligence (AI) is having a multifaceted impact on job prospects in hardware design, including for those specializing in combinational circuits. Increased Demand in AI Hardware: One of the most significant effects is the creation of new opportunities in designing specialized hardware for AI. AI algorithms, particularly deep learning, are computationally intensive. This has spurred a massive demand for AI accelerators (GPUs, TPUs, FPGAs configured for AI, and custom ASICs) that can perform these computations efficiently. Engineers who can design the combinational and sequential logic for these specialized chips are in high demand. This is a growing area with strong job prospects. AI Tools for Hardware Design: AI is also starting to be used as a tool *within* the hardware design process itself. AI and machine learning techniques are being explored for tasks such as: * Logic synthesis and optimization * Circuit verification and testing * Physical layout and routing * Predicting performance and power consumption While these AI tools aim to automate or augment parts of the design flow, they are unlikely to replace hardware designers entirely. Instead, designers may need to learn how to effectively use these AI-powered EDA tools. This could shift some job roles towards working alongside AI, guiding its processes, and verifying its outputs. It might also free up engineers to focus on more creative, architectural, and system-level design challenges. Shift in Skill Requirements: For some roles, there might be an increasing need for hardware designers to have some understanding of AI algorithms and workloads to design more effective AI-specific hardware. Conversely, AI researchers with an understanding of hardware limitations can develop more hardware-friendly algorithms. Overall, while AI might automate some routine tasks, it is also creating significant new demand for hardware designers, especially those who can contribute to the development of next-generation AI systems or leverage AI tools to improve design efficiency. The fundamental skills in combinational logic and digital design remain crucial as they form the bedrock upon which these advanced systems are built.

Are freelance opportunities common in this domain?

Freelance opportunities in core combinational circuit design, especially for complex ASIC or FPGA projects, are less common than in fields like software development or web design. This is due to several factors: * High Cost of Tools: Professional EDA software licenses for ASIC and advanced FPGA design can be prohibitively expensive for individual freelancers. * Need for Specialized Equipment: Testing and validating hardware often requires access to sophisticated laboratory equipment (oscilloscopes, logic analyzers, spectrum analyzers, etc.). * Intellectual Property (IP) Concerns: Companies are often very protective of their hardware designs and IP, making them hesitant to outsource core design work to individual freelancers, especially for sensitive projects. * Complexity and Teamwork: Modern digital design projects are often very complex and require teams of engineers with diverse specializations working closely together. * Long Project Cycles: Hardware development cycles can be long, which might not always fit well with typical freelance engagement models. However, freelance or contract opportunities can exist in certain niches: * FPGA Prototyping and Niche Applications: For smaller companies or specific projects involving FPGAs, there might be opportunities for experienced freelance FPGA designers, especially if the work can be done remotely with more accessible development boards and open-source or lower-cost tools. * Embedded Systems Design and Firmware: Freelancers with skills in both hardware (including digital logic for interfacing) and firmware development for embedded systems may find more opportunities, as these projects can sometimes be more self-contained. * Consulting: Highly experienced engineers might offer consulting services on specific aspects of digital design, verification, or system architecture. * Technical Writing and Training: Opportunities may exist for creating documentation, training materials, or online courses related to digital logic and hardware design. * Verification Services: Some aspects of design verification might be contracted out, though often to specialized verification service companies rather than individual freelancers. For those interested in freelance work in this broader area, focusing on skills that are amenable to remote work and don't require massive capital outlay for tools is generally more viable. Building a strong network and a portfolio of successful projects is crucial for securing such opportunities.

Useful Links and Resources

To further your exploration of combinational circuits and digital electronics, here are some helpful resources: * OpenCourser: Explore a wide range of courses in Engineering and Computer Science. Use the search functionality to find courses on "digital logic," "VHDL," "Verilog," or "computer architecture." The OpenCourser Learner's Guide can provide valuable tips on how to make the most of online learning. * NIST (National Institute of Standards and Technology): For information on semiconductor manufacturing and its environmental impact, resources like the article on Understanding Semiconductors and Their Environmental Impact can be insightful. * Online Communities: * EEWeb Community * All About Circuits Forum * Stack Exchange (Electrical Engineering, Computer Science) * Reddit (r/ECE, r/FPGA, r/AskElectronics) * Open-Source Tools: * Logisim Evolution (a maintained fork of Logisim) * Icarus Verilog * GHDL (Gnu VHDL)

Embarking on a journey to understand combinational circuits can be both challenging and deeply rewarding. Whether you are a student, a professional looking to upskill, or simply a curious mind, the world of digital logic offers endless opportunities for learning and innovation. With dedication and the right resources, you can unlock the principles that power much of our modern technological world. Good luck on your learning path!