A Comprehensive Guide to Analytic Geometry

Analytic geometry, also known as coordinate geometry or Cartesian geometry, is a captivating branch of mathematics that elegantly weds algebra with geometry. It provides a framework for defining and representing geometric shapes using numerical coordinates and algebraic equations, allowing for the extraction of numerical information from these representations. This field serves as a foundational pillar for numerous modern areas of geometry and has far-reaching applications across various disciplines. Imagine describing the curve of a satellite's orbit or the precise movements of a robotic arm – these are among the fascinating challenges that analytic geometry helps solve. The ability to translate spatial relationships into the language of equations opens up a world of analytical power and precise modeling.

At its core, analytic geometry allows us to locate any point in a plane or in three-dimensional space using an ordered pair or triplet of numbers, respectively, known as coordinates. This system, most commonly the Cartesian coordinate system, enables the manipulation of equations for planes, lines, circles, and more complex figures. The beauty of this approach lies in its power to transform geometric problems into algebraic ones, and vice versa, offering a versatile toolkit for investigation and problem-solving. For those intrigued by the interplay of visual shapes and symbolic logic, or for individuals looking to apply mathematical principles to real-world scenarios, analytic geometry offers an engaging and intellectually stimulating path.

What is Analytic Geometry?

Analytic geometry is the study of geometry using a coordinate system. This simple definition belies a powerful idea: that geometric shapes—lines, circles, parabolas, ellipses, and even more complex curves and surfaces—can be described and analyzed using algebraic equations. Conversely, algebraic equations can be visualized as geometric shapes. This two-way street between algebra and geometry is the hallmark of this mathematical field.

Consider a simple line. In synthetic geometry (the geometry you might have learned with compass and straightedge), a line is an undefined primitive concept. In analytic geometry, a line in a two-dimensional plane can be precisely defined by an equation like y = mx + b, where m represents the slope and b the y-intercept. Every point on that line will have coordinates (x, y) that satisfy this equation, and every pair of coordinates (x, y) that satisfies the equation corresponds to a point on that line. This allows for a numerical and algebraic approach to understanding geometric properties.

The fundamental tool of analytic geometry is the coordinate system, most famously the Cartesian coordinate system, named after its inventor, René Descartes. This system uses two perpendicular axes (the x-axis and y-axis in two dimensions, with an added z-axis for three dimensions) to define the position of any point with a set of numerical coordinates. This framework allows mathematicians and scientists to define geometric figures, calculate distances, find slopes, determine angles, and explore relationships between shapes with algebraic rigor.

Definition and Historical Significance

Analytic geometry is the branch of mathematics that employs algebraic methods and coordinate systems to study geometric figures. It establishes a direct correspondence between algebraic equations and geometric shapes, allowing for the numerical representation and analysis of these shapes. For example, a circle with its center at the origin (0,0) and a radius 'r' can be represented by the equation x² + y² = r². Any point (x,y) satisfying this equation lies on the circle.

The historical significance of analytic geometry is immense, largely attributed to the work of French philosopher and mathematician René Descartes in the 17th century. His publication "La Géométrie" in 1637 is considered a landmark, introducing the Cartesian coordinate system and systematically applying algebraic methods to geometry. This innovation revolutionized mathematics by bridging the gap between what were then two largely separate disciplines: algebra and geometry. Pierre de Fermat, another prominent French mathematician, independently developed similar concepts around the same time.

Before analytic geometry, geometric problems were primarily solved using synthetic methods, relying on axioms, postulates, and logical deductions without the use of coordinates or explicit algebraic formulas. The advent of analytic geometry provided a powerful new toolkit, enabling the solution of a broader range of geometric problems, often with greater ease and generality. It laid crucial groundwork for the subsequent development of calculus by Isaac Newton and Gottfried Wilhelm Leibniz, as it provided the means to describe functions and curves in a way that could be subjected to the operations of differentiation and integration.

Relationship Between Algebra and Geometry

The core of analytic geometry lies in its powerful fusion of algebra and geometry, creating a symbiotic relationship where each field enhances the understanding and capabilities of the other. Geometry provides a visual and intuitive way to understand algebraic concepts. For instance, the solutions to a system of linear equations can be visualized as the intersection point(s) of their corresponding lines or planes. An equation like y = x² isn't just an abstract algebraic statement; it's the elegant curve of a parabola on a coordinate plane.

Conversely, algebra provides precise tools for analyzing and manipulating geometric figures. Geometric properties such as slope, distance, parallelism, perpendicularity, and the nature of curves can be expressed and investigated using algebraic equations and formulas. This allows for a level of precision and computational power that is often difficult to achieve through purely geometric reasoning (synthetic geometry). For example, proving that the diagonals of a rhombus are perpendicular can be done by assigning coordinates to its vertices and using algebraic formulas for slopes.

This interplay is fundamental. Geometric intuition can guide algebraic manipulation, and algebraic rigor can confirm or refine geometric insights. This powerful combination has made analytic geometry an indispensable tool in mathematics and its applications, providing a language to describe and solve problems that involve both spatial and quantitative aspects.

Key Applications Across Disciplines

Analytic geometry is not just an abstract mathematical exercise; its principles are fundamental to numerous fields, demonstrating its profound real-world utility. In engineering, it's used extensively for design and analysis. For example, engineers use analytic geometry to design the curves of roads, the shapes of aircraft wings for optimal aerodynamics, or the structural components of buildings and bridges, ensuring stability and efficiency. Computer-Aided Design (CAD) systems, which are indispensable in modern engineering and architecture, are built upon the principles of analytic geometry to represent and manipulate 2D and 3D objects.

Physics relies heavily on analytic geometry to describe the motion of objects and the behavior of forces. The trajectory of a projectile, the orbit of a planet, or the paths of subatomic particles can be modeled and analyzed using equations within a coordinate system. NASA, for example, uses analytic geometry extensively to calculate spacecraft trajectories and orbits.

Computer graphics, a field that powers everything from video games and animated movies to scientific visualizations and user interfaces, is fundamentally based on analytic geometry. Objects are represented as collections of points (vertices) defined by their coordinates, and transformations like scaling, rotation, and translation are performed using algebraic operations on these coordinates. The rendering of 3D scenes onto a 2D screen also involves sophisticated geometric calculations. Furthermore, fields like cartography (map-making and GPS systems), robotics (for navigation and manipulation), and even medicine (e.g., locating kidney stones for treatment) utilize its concepts.

For those interested in exploring these foundational concepts, online resources can be very helpful. You can begin your journey by exploring courses available on OpenCourser's mathematics section.

Basic vs. Advanced Analytic Geometry

Analytic geometry spans a wide range of complexity, from concepts typically introduced in high school to highly advanced topics explored in university mathematics and research.

Basic analytic geometry primarily deals with the Cartesian coordinate system in two dimensions (the plane) and, to some extent, in three dimensions (space). Key topics at this level include plotting points, calculating the distance between two points, finding the midpoint of a line segment, determining the slope of a line, and writing equations for lines in various forms (e.g., slope-intercept, point-slope). It also introduces the conic sections—circles, parabolas, ellipses, and hyperbolas—and their standard equations. These foundational concepts are crucial for understanding functions, graphs, and basic geometric transformations.

Advanced analytic geometry builds upon these fundamentals, delving into more complex curves and surfaces, coordinate transformations (like rotation and translation of axes), and the use of parametric equations and polar coordinates. It explores vector geometry, which uses vectors to represent quantities with both magnitude and direction, and its applications in describing lines, planes, and their interactions in 3D space. Topics like the dot product and cross product of vectors become important tools. Furthermore, advanced analytic geometry serves as a crucial stepping stone to higher-level mathematics such as multivariable calculus, differential geometry (which studies curves and surfaces using calculus), and linear algebra (which generalizes vector spaces). It also plays a role in areas like algebraic geometry, which studies the solutions of polynomial equations using abstract algebraic techniques.

To build a solid foundation, consider starting with a comprehensive pre-calculus course.

We think this course offers a good preparation by covering essential mathematical subjects needed for more advanced studies.

Historical Development

The roots of geometric thought extend back to ancient civilizations like Egypt, Babylonia, and Greece. Euclid's "Elements" (circa 300 BC) provided a systematic, axiomatic approach to geometry that dominated for centuries. [7rxv7e] However, the idea of merging algebra with geometry to the extent seen in analytic geometry was a much later development.

While ancient Greek mathematicians like Apollonius of Perga studied conic sections in great depth, their methods were purely geometric. The conceptual leap to represent geometric figures with algebraic equations and to use a coordinate system to define points numerically is the defining characteristic of analytic geometry. This revolution in mathematical thought is primarily credited to thinkers of the 17th century.

Understanding this historical evolution provides valuable context for appreciating the power and elegance of modern analytic geometry and its widespread applications.

Descartes' Foundational Contributions

The birth of analytic geometry as a formal discipline is overwhelmingly attributed to the French philosopher, mathematician, and scientist René Descartes (1596-1650). In his seminal work, "La Géométrie," published in 1637 as an appendix to his "Discours de la Méthode" (Discourse on the Method), Descartes introduced a systematic way to apply algebraic methods to geometric problems. He famously developed the coordinate system that now bears his name: the Cartesian coordinate system. This system allows any point in a plane (or in space) to be uniquely identified by a pair (or triplet) of numbers.

Descartes' key insight was that by establishing this correspondence between points and numbers, geometric curves could be represented by algebraic equations involving these coordinates. For example, he showed how lines, circles, and other curves could be expressed as equations in x and y. This allowed geometric problems to be translated into algebraic problems, which could then be solved using the tools of algebra. Conversely, algebraic equations could be interpreted geometrically, providing a visual understanding of their behavior.

While Descartes viewed geometry as the fundamental mathematical science and saw his algebraic techniques as an extension of constructive geometric methods, his work fundamentally changed the landscape of mathematics. It provided a powerful and unified framework that paved the way for countless advancements, most notably the development of calculus. His work also introduced algebraic notation that is still in use today, such as using x, y, and z for unknowns and a, b, and c for constants.

These books delve into the foundational texts and concepts related to geometry and its development.

Evolution Through 17th-19th Centuries

Following Descartes' groundbreaking work, analytic geometry rapidly developed throughout the 17th, 18th, and 19th centuries, with numerous mathematicians building upon and extending his ideas. Pierre de Fermat, a contemporary of Descartes, independently developed many similar concepts in analytic geometry, though his work was published posthumously. His contributions included methods for finding maxima, minima, and tangents to curves, which were also crucial precursors to calculus.

The 17th century also saw the invention of calculus by Isaac Newton and Gottfried Wilhelm Leibniz, a development deeply intertwined with analytic geometry. Analytic geometry provided the language and framework (functions, curves, coordinates) upon which calculus could operate to study rates of change and accumulation. Mathematicians like Leonhard Euler in the 18th century made extensive use of analytic geometry, further developing the theory of curves and surfaces, and applying it to mechanics and other areas of physics. Euler was instrumental in standardizing notation and formalizing many concepts in both analytic geometry and calculus.

The 19th century witnessed further generalizations and abstractions. The development of non-Euclidean geometries by mathematicians like Lobachevsky, Bolyai, and Riemann challenged traditional geometric notions and showed that different geometric systems could be consistently developed. Analytic methods were crucial in exploring these new geometries. Projective geometry, which studies properties of geometric figures that are invariant under projection, also saw significant development during this period, with figures like Jean-Victor Poncelet and Julius Plücker making key contributions. Plücker, for instance, introduced the concept of line coordinates and extensively used algebraic methods. This era also laid the groundwork for higher-dimensional geometry and the development of vector analysis, further expanding the scope and power of analytic geometry.

Modern Computational Adaptations

In the 20th and 21st centuries, the principles of analytic geometry have been powerfully adapted and extended through the rise of computers. Computational geometry, a subfield of computer science, emerged in the late 1970s and focuses on designing algorithms to solve geometric problems. This field heavily relies on the foundational concepts of analytic geometry, such as coordinate systems, vector operations, and equations of geometric objects, to develop efficient methods for tasks crucial in many application domains.

Modern applications like Computer-Aided Design (CAD), Computer-Aided Manufacturing (CAM), robotics, computer graphics, Geographic Information Systems (GIS), and molecular modeling all depend on the computational implementation of analytic geometry. For instance, creating realistic 3D models in video games or animations involves defining objects as meshes of polygons (often triangles), where the vertices of these polygons are specified by their 3D coordinates. Transformations (scaling, rotation, translation), lighting effects, and perspective projections are all calculated using matrix algebra and vector operations rooted in analytic geometry.

The ability to perform vast numbers of geometric calculations quickly and accurately has opened up new possibilities. Complex simulations, such as modeling airflow over a wing or the folding of proteins, rely on representing and manipulating geometric data. Algorithms for tasks like collision detection (determining if two objects in a virtual environment are intersecting), path planning for robots, and spatial data analysis in GIS all have their theoretical underpinnings in analytic geometry. The development of powerful software libraries and graphics processing units (GPUs) has further democratized access to these computational tools, making sophisticated geometric modeling and analysis accessible across many scientific and engineering disciplines.

These texts provide insights into how calculus and analytic geometry are often taught and applied together, reflecting modern approaches.

Core Concepts and Principles of Analytic Geometry

To truly grasp analytic geometry, one must become familiar with its fundamental building blocks. These concepts form the language used to describe and analyze geometric objects algebraically. Mastering these principles is essential for anyone wishing to apply analytic geometry in various fields or to progress to more advanced mathematical studies.

At the heart of it all is the idea of assigning numerical addresses (coordinates) to points, which then allows us to translate geometric shapes and relationships into algebraic equations and expressions. This section will delve into some of the most crucial of these core concepts.

If you are looking for comprehensive courses that cover these core mathematical concepts, OpenCourser offers a variety of options. You can use the OpenCourser search functionality to find courses tailored to "analytic geometry" or "coordinate geometry."

Cartesian Coordinate Systems

The Cartesian coordinate system, named after René Descartes, is the cornerstone of analytic geometry. In its most common two-dimensional form, it consists of two perpendicular lines, called axes, that intersect at a point called the origin. The horizontal axis is typically labeled the x-axis, and the vertical axis is the y-axis. Each point in the plane can then be uniquely identified by an ordered pair of numbers (x, y), where 'x' represents the directed distance from the y-axis (the x-coordinate or abscissa) and 'y' represents the directed distance from the x-axis (the y-coordinate or ordinate).

This system extends naturally to three dimensions by adding a third axis, the z-axis, perpendicular to both the x and y-axes and passing through the origin. A point in three-dimensional space is then represented by an ordered triplet (x, y, z). The coordinate axes divide the plane into four quadrants (in 2D) or space into eight octants (in 3D), characterized by the signs of the coordinates.

The power of the Cartesian system lies in its ability to provide a unique numerical address for every geometric point, thereby allowing geometric figures (collections of points) to be described by algebraic equations relating these coordinates. For instance, all points on a line will satisfy a specific linear equation, and all points on a circle will satisfy a specific quadratic equation. This numerical representation is what enables the algebraic manipulation and analysis of geometric shapes.

To get a practical feel for these concepts, consider exploring introductory courses. The following courses cover the basics of trigonometry and analytic geometry, which often go hand-in-hand.

These courses provide a good starting point for understanding the essentials of analytic geometry in Spanish, with a focus on pre-university level mathematics.

ELI5: Cartesian Coordinate Systems

Imagine you have a giant piece of graph paper. This graph paper is your "plane." Now, pick a special spot right in the middle and call it the "origin" – this is like your home base (0,0).

To find any other spot on this paper, you need two instructions: first, how many steps to take left or right from home base, and second, how many steps to take up or down. The "left or right" line is called the x-axis, and the "up or down" line is called the y-axis. When you write down these two numbers, like (3 steps right, 2 steps up), that's the coordinate of your spot! So, (3,2) tells anyone exactly where to find that spot on your giant graph paper. That's all a Cartesian coordinate system is – a way to give every spot an address using numbers so we can talk about them with math.

Equations of Lines and Conic Sections

A fundamental aspect of analytic geometry is representing geometric shapes with algebraic equations. Lines are among the simplest yet most important geometric figures. In a two-dimensional Cartesian plane, a straight line can be represented by a linear equation, typically in the form Ax + By + C = 0 (general form) or y = mx + b (slope-intercept form), where m is the slope of the line and b is the y-intercept (the y-coordinate where the line crosses the y-axis). Different forms are useful for different purposes; for example, if you know two points on a line, you can use the two-point form to find its equation.

Conic sections are another significant class of curves studied in analytic geometry. These are curves obtained by intersecting a cone with a plane at different angles. They include the circle, ellipse, parabola, and hyperbola. Each of these conic sections has a standard algebraic equation of the second degree in x and y. For example, a circle centered at (h, k) with radius r has the equation (x-h)² + (y-k)² = r². A parabola might be y² = 4ax or x² = 4ay. Ellipses and hyperbolas have slightly more complex standard forms. Understanding these equations allows for the detailed analysis of the properties and behaviors of these important geometric shapes.

The ability to describe these fundamental shapes with equations is a cornerstone of applying mathematical principles to fields like physics (planetary orbits are often elliptical), engineering (parabolic reflectors), and optics (lenses can have spherical or aspherical surfaces).

These books offer a classical treatment of analytic geometry, often combining it with calculus, and are valuable for understanding the equations of lines and conic sections in depth.

Distance Formulas and Locus Problems

One of the most basic and useful tools in analytic geometry is the distance formula. Derived from the Pythagorean theorem, it allows us to calculate the straight-line distance between any two points in a coordinate plane (or in space). In a two-dimensional plane, if you have two points P₁(x₁, y₁) and P₂(x₂, y₂), the distance 'd' between them is given by the formula: d = √((x₂ - x₁)² + (y₂ - y₁)²). A similar formula exists for three dimensions, incorporating the z-coordinates.

The concept of distance is fundamental to solving many geometric problems and leads directly to the idea of a locus. A locus is a set of points that satisfy a given geometric condition or property. Many geometric figures can be defined as loci. For example, a circle is the locus of points in a plane that are equidistant from a fixed point (the center). A parabola is the locus of points that are equidistant from a fixed point (the focus) and a fixed line (the directrix). Using the distance formula and algebraic manipulation, we can derive the equation of a locus, which is the algebraic representation of the geometric figure defined by the condition.

Locus problems are a classic type of problem in analytic geometry that involves finding the equation of a curve or surface that satisfies certain geometric constraints. These problems help to solidify the connection between geometric descriptions and algebraic equations, forming a core skill in the application of analytic geometry.

Coordinate Transformations

Coordinate transformations are operations that change the coordinate system used to describe geometric objects, without changing the objects themselves or their relationships to each other. These transformations are powerful tools in analytic geometry because they can simplify the equations of curves and surfaces, making them easier to analyze and understand. The two most common types of transformations are translation and rotation of axes.

Translation of axes involves shifting the origin of the coordinate system to a new point (h, k) without changing the orientation (direction) of the axes. If a point P has coordinates (x, y) in the original system and (x', y') in the new system whose origin is at (h, k) relative to the old system, then the transformation equations are x = x' + h and y = y' + k, or conversely, x' = x - h and y' = y - k. This transformation is often used to simplify equations of conic sections by moving the origin to the center (for ellipses and hyperbolas) or vertex (for parabolas).

Rotation of axes involves rotating the x and y axes by a certain angle θ about the origin, while keeping the origin fixed. If a point P has coordinates (x, y) in the original system and (x', y') in the new, rotated system, the transformation equations are more complex, involving trigonometric functions of θ: x = x' cos(θ) - y' sin(θ) y = x' sin(θ) + y' cos(θ) Rotation is particularly useful for eliminating the xy-term in the general second-degree equation Ax² + Bxy + Cy² + Dx + Ey + F = 0, which allows for easier identification and analysis of a conic section whose axes are not parallel to the coordinate axes. Mastering coordinate transformations significantly enhances one's ability to work with geometric figures in various orientations and positions.

Applications in Modern Fields

The principles of analytic geometry are not confined to textbooks; they are actively applied in a multitude of modern fields, driving innovation and solving complex problems. Its ability to model spatial relationships with mathematical precision makes it an invaluable tool across science, technology, engineering, and even economics. The transition from theoretical concepts to practical applications highlights the enduring relevance and power of this mathematical discipline.

From designing intricate machinery to creating breathtaking visual effects in movies, analytic geometry provides the fundamental language and tools. Understanding these applications can provide strong motivation for students and offer career explorers insights into how mathematical skills translate into tangible outcomes in various industries. For those looking to explore a wide array of courses that touch upon these applied areas, the browse page on OpenCourser is an excellent resource.

Engineering Design and CAD Systems

Analytic geometry is foundational to engineering design and the operation of Computer-Aided Design (CAD) systems. Engineers in various disciplines—mechanical, civil, aerospace, and electrical—rely on geometric principles to conceptualize, design, analyze, and manufacture products and structures. For instance, when designing a new car body, engineers use analytic geometry to define the precise curves and surfaces that determine its aerodynamic properties and aesthetic appeal. Similarly, in civil engineering, the design of bridges, tunnels, and road networks involves complex geometric calculations to ensure structural integrity, safety, and optimal functionality.

CAD software, which is ubiquitous in modern engineering, is essentially a sophisticated application of analytic geometry. These systems allow engineers to create detailed 2D drawings and 3D models of objects. Within a CAD environment, points are defined by coordinates, lines by equations, and surfaces by more complex mathematical representations (e.g., NURBS - Non-Uniform Rational B-Splines). Operations such as scaling, rotating, translating, and combining objects are all performed using underlying algebraic and geometric algorithms derived from analytic geometry. This precise mathematical representation enables accurate simulations, stress analysis, and the generation of instructions for manufacturing processes like 3D printing or CNC machining.

The course referenced below, while focused on pre-university calculus, often includes elements of analytic geometry crucial for engineering foundations.

Physics Simulations and Modeling

In the realm of physics, analytic geometry is indispensable for modeling physical phenomena and conducting simulations. Physicists use coordinate systems and geometric equations to describe the motion of particles, the propagation of waves, the interactions of forces, and the structure of fields. For example, the trajectory of a projectile under gravity can be modeled as a parabolic path, whose equation is derived using principles of analytic geometry and kinematics. The orbits of planets and satellites around celestial bodies are often elliptical, described by precise mathematical equations that allow for prediction and analysis.

Simulations in physics, ranging from modeling the behavior of galaxies to understanding fluid dynamics or the interactions of subatomic particles, rely heavily on representing objects and their environments within a geometric framework. Analytic geometry provides the tools to define spatial relationships, calculate distances and angles, and track changes in position and orientation over time. For instance, in simulating the collision of two particles, their paths, impact parameters, and resulting trajectories are all analyzed using geometric and algebraic methods. Many complex physical systems are modeled by discretizing space and objects into smaller, manageable geometric elements (like in finite element analysis), where interactions are calculated based on their geometric configurations and physical laws.

To explore these concepts further, consider a course that bridges mathematics and engineering applications, such as vector calculus.

This course delves into vector calculus, which builds upon analytic geometry and is essential for many physics and engineering models.

Computer Graphics Algorithms

Analytic geometry is the mathematical backbone of computer graphics, influencing everything from the generation of simple 2D shapes to the rendering of complex 3D virtual worlds. At its core, computer graphics involves representing geometric objects numerically and manipulating these representations to create images on a screen. Points in 2D or 3D space are defined by their coordinates (x, y) or (x, y, z). Lines, polygons, curves (like Bézier curves and splines), and surfaces are then constructed from these points and described by mathematical equations.

Key computer graphics algorithms heavily rely on analytic geometry. Transformations such as translation (moving an object), rotation (turning an object), and scaling (resizing an object) are implemented using matrix operations applied to the coordinates of the object's vertices. Projection, the process of transforming a 3D scene into a 2D image for display, involves complex geometric calculations to determine how objects appear from a specific viewpoint, considering perspective and depth. Hidden surface determination (figuring out which surfaces are visible and which are obscured by others), lighting and shading models (calculating how light interacts with surfaces to create realistic appearances), and collision detection in animations and games all require robust geometric computations. Even the rasterization process, which converts vector graphics into pixels on a screen, involves determining which pixels lie within the boundaries of geometric primitives.

Economic Forecasting Models

While perhaps less direct than in engineering or computer graphics, analytic geometry and its related mathematical concepts also find applications in economic forecasting and modeling. Economists often use graphs to represent relationships between economic variables, such as supply and demand curves, indifference curves, or production possibility frontiers. These graphical representations are inherently based on coordinate systems where axes represent different economic quantities. The shapes and intersections of these curves, analyzed using geometric and algebraic techniques, provide insights into market equilibrium, consumer behavior, and optimal resource allocation.

In econometrics, which applies statistical methods to economic data, geometric interpretations can be useful. For instance, linear regression, a common technique for finding the relationship between variables, can be visualized as fitting a line (or hyperplane in higher dimensions) to a scatter plot of data points. The concepts of distance and projection are used in understanding the properties of estimators. Some advanced economic models, particularly in general equilibrium theory, may involve more complex geometric or topological structures. While many forecasting models rely more heavily on time series analysis and stochastic processes, the visualization and interpretation of data and model outputs often benefit from a geometric understanding. For instance, understanding trends and patterns in data plotted over time can sometimes be aided by identifying geometric shapes or slopes that might indicate growth rates or turning points.

For foundational mathematical skills applicable to economics, courses covering elements of calculus, linear algebra, and statistics are beneficial. Many general mathematics or pre-university math courses include aspects of analytic geometry that are useful.

These courses, while not exclusively focused on economic forecasting, provide mathematical foundations that are broadly applicable in economics and other quantitative fields.

Formal Education Pathways

For individuals aspiring to delve deeply into analytic geometry, whether for academic pursuits, research, or specialized careers, a structured educational journey is typically undertaken. This path often begins in secondary school and can extend through undergraduate and graduate studies, with each stage building upon the knowledge and skills acquired previously.

Understanding the typical progression can help students plan their studies and make informed decisions about their educational goals. Moreover, it highlights the interconnectedness of mathematical topics and the importance of a strong foundation.

High School Prerequisite Courses

A solid foundation in mathematics at the high school level is crucial for success in analytic geometry and subsequent advanced studies. Typically, a sequence of algebra courses (Algebra I and Algebra II) is essential. These courses introduce students to manipulating algebraic expressions, solving equations and inequalities, understanding functions, and working with polynomials – all of which are fundamental tools in analytic geometry.

A dedicated course in geometry, usually taken between Algebra I and Algebra II or concurrently with Algebra II, is also a key prerequisite. While this often focuses on synthetic geometry (proofs, theorems, constructions), it develops spatial reasoning and familiarity with geometric shapes and properties that are later analyzed using algebraic methods. Topics like parallel lines, triangles, quadrilaterals, circles, and basic transformations are important.

Finally, Precalculus or a course that combines trigonometry and advanced algebra serves as the immediate preparatory step before or alongside a formal introduction to analytic geometry. Trigonometry is vital for understanding angles, rotations, and relationships in triangles, which are frequently encountered in analytic geometry, especially in topics like coordinate transformations and vector analysis. [sg9tra] A strong grasp of functions, including polynomial, rational, exponential, and logarithmic functions, is also critical. Some high schools might offer analytic geometry as a distinct course, while others integrate its core concepts within Precalculus or Calculus curricula.

These courses, available in Spanish, cover high school and pre-university level mathematics, including trigonometry and analytic geometry, making them excellent preparatory resources.

Undergraduate Mathematics Curricula

In undergraduate mathematics programs, analytic geometry often serves as a foundational component, typically integrated within the early calculus sequence (Calculus I, II, and III). [lhbtw5, 9qdcuj] Calculus I usually revisits and extends concepts of functions, limits, derivatives, and integrals, all of which are often introduced and visualized using the Cartesian coordinate system. Analytic geometry provides the framework for understanding curves, tangents, areas, and volumes that are central to calculus.

Calculus II often delves deeper into techniques of integration, sequences, and series, and may include more advanced topics from analytic geometry like parametric equations, polar coordinates, and more detailed study of conic sections. Calculus III (Multivariable Calculus) heavily relies on three-dimensional analytic geometry. Topics such as vectors in 2D and 3D, dot and cross products, equations of lines and planes in space, quadratic surfaces, and cylindrical and spherical coordinate systems are core components. [y2x0t0]

Beyond the calculus sequence, concepts from analytic geometry are implicitly or explicitly used in courses like Linear Algebra (which formalizes vector spaces, matrices, and linear transformations) [yfqjj3] and Differential Equations. Some universities might offer dedicated courses in geometry that include advanced analytic geometry, projective geometry, or an introduction to differential geometry, which applies calculus to study curves and surfaces. For students specializing in applied mathematics, physics, or engineering, the applications of analytic geometry are further explored in their respective specialized courses.

These books are standard texts often used in undergraduate calculus and analytic geometry courses, providing a comprehensive theoretical basis.

Graduate-Level Research Opportunities

At the graduate level, while analytic geometry as a standalone research field is less common (as its foundational principles are well-established), its concepts and techniques become integral tools in more specialized areas of mathematical research. Students pursuing a Master's or Ph.D. in mathematics might encounter advanced geometric concepts in fields like Algebraic Geometry, Differential Geometry, Topology, and Geometric Analysis.

Algebraic Geometry, for example, studies geometric objects defined by polynomial equations using sophisticated algebraic machinery. While it moves far beyond the scope of introductory analytic geometry, its roots are firmly planted in the idea of describing geometry through algebra. Differential Geometry applies the tools of calculus (including multivariable calculus, which heavily uses 3D analytic geometry) to study the properties of curves, surfaces, and higher-dimensional manifolds. [iehrm9] This field has significant applications in theoretical physics, particularly in general relativity and string theory.

Topology is a more abstract field concerned with the properties of spaces that are preserved under continuous deformations. While seemingly distant, certain branches of topology, like geometric topology, can involve analytic and geometric techniques. Furthermore, research in areas like computational geometry, geometric modeling, and scientific computing often requires a deep understanding of analytic geometry and its computational aspects, leading to research in developing new algorithms and techniques for solving complex geometric problems encountered in various scientific and engineering disciplines. Opportunities may also arise in mathematical physics, where geometric methods are crucial for formulating and solving physical theories.

This book touches upon more advanced concepts relevant to graduate-level geometry.

Self-Directed Learning Strategies

For those looking to learn analytic geometry outside of traditional academic settings, such as career changers or independent learners, a structured approach to self-directed learning can be highly effective. The wealth of online resources, textbooks, and communities makes it more accessible than ever to master this fascinating subject at your own pace.

A key to success in self-study is to build a solid foundation, engage actively with the material, and seek out opportunities to apply what you've learned. The flexibility of self-directed learning allows you to tailor your study plan to your specific goals and interests, whether it's for personal enrichment, career advancement, or bridging knowledge gaps.

OpenCourser's Learner's Guide offers valuable articles on how to create a structured curriculum for yourself and remain disciplined when self-learning, which can be particularly helpful for independent learners.

Recommended Prerequisite Skills

Before diving into analytic geometry, ensuring you have a firm grasp of certain prerequisite mathematical skills will significantly smooth your learning journey. First and foremost is a strong foundation in algebra. This includes proficiency in manipulating algebraic expressions, solving linear and quadratic equations, working with inequalities, and understanding the concept of functions, including their notation and graphing. Familiarity with polynomial, rational, exponential, and logarithmic functions is also beneficial.

A good understanding of basic geometry concepts is also essential. This means being comfortable with properties of lines, angles, triangles, quadrilaterals, and circles. While analytic geometry provides an algebraic approach to these figures, prior geometric intuition is invaluable. Knowledge of the Pythagorean theorem is particularly crucial, as it forms the basis for the distance formula, a cornerstone of analytic geometry.

Finally, a working knowledge of trigonometry is highly recommended, especially if you plan to explore topics beyond basic 2D analytic geometry. Understanding trigonometric functions (sine, cosine, tangent), their graphs, identities, and the unit circle will be important for dealing with angles, rotations, polar coordinates, and vectors. Many online platforms offer courses to refresh or build these foundational skills. Consider searching for "algebra fundamentals," "geometry basics," or "trigonometry review" on OpenCourser to find suitable preparatory material.

Project-Based Learning Approaches

Engaging in project-based learning can be a highly effective and motivating way to learn analytic geometry. Instead of solely focusing on abstract exercises, projects allow you to apply concepts to solve tangible problems or create interesting outputs, thereby deepening your understanding and retention. For example, you could start with a project to model a simple physical system, like the trajectory of a ball thrown in the air using parabolic equations.

Another project idea could be to create a basic 2D graphics engine. This would involve using analytic geometry to define shapes (lines, polygons, circles), implement transformations (translation, rotation, scaling), and perhaps even basic clipping (determining what part of a shape is visible within a window). Even a simple game, like a 2D shooter where you need to calculate trajectories of projectiles and detect collisions, can provide a rich context for applying distance formulas, equations of lines, and intersection calculations.

You could also explore projects related to data visualization, such as plotting datasets and fitting lines or curves to them. For those interested in design, try modeling a real-world object using combinations of basic geometric shapes described by their equations. The key is to choose projects that are challenging yet achievable, allowing you to see the practical power of analytic geometry in action. Online communities and forums can be great places to find project ideas and get feedback.

Open-Source Tools and Software

Several open-source tools and software can greatly aid in the self-directed learning of analytic geometry by providing environments for visualization, computation, and experimentation. GeoGebra is a highly popular and versatile open-source mathematics software that combines geometry, algebra, spreadsheets, graphing, statistics, and calculus in one easy-to-use package. It allows users to construct geometric figures, plot functions and equations, and dynamically explore their properties. This visual and interactive approach can make abstract concepts much more concrete.

For those interested in more programming-oriented tools, Python, with libraries such as NumPy (for numerical operations) and Matplotlib (for plotting), offers a powerful environment for implementing analytic geometry concepts. You can write scripts to calculate distances, find equations of lines, plot conic sections, perform transformations, and even create simple animations. GNU Octave or Scilab are open-source alternatives to MATLAB, providing robust numerical computation capabilities suitable for more complex geometric calculations and simulations.

Additionally, computer algebra systems (CAS) like Maxima or SymPy (a Python library for symbolic mathematics) can help with algebraic manipulations, solving equations, and simplifying expressions, which are often part of analytic geometry problems. Using these tools not only aids in understanding the concepts but also develops valuable computational skills that are highly relevant in many STEM fields.

Community Problem-Solving Forums

Engaging with online communities and problem-solving forums can be an invaluable resource for self-directed learners of analytic geometry. Platforms like Stack Exchange (particularly Mathematics Stack Exchange), Reddit (e.g., r/learnmath, r/askmath), and forums associated with specific MOOCs or learning platforms provide spaces where you can ask questions, seek clarification on difficult concepts, and see how others approach problems.

When you encounter a challenging problem or a concept you don't fully understand, trying to articulate your question clearly for a forum can itself be a learning experience. Reading answers and explanations from more experienced individuals or peers can offer new perspectives and insights. Furthermore, attempting to help others by answering their questions (once you feel comfortable with certain topics) is an excellent way to solidify your own understanding and identify any gaps in your knowledge.

Many of these communities also discuss applications of mathematics, share learning resources, and provide encouragement. Participating in problem-solving challenges or discussions about specific theorems or techniques can make the learning process more interactive and less isolating. Remember to always be respectful and follow the community guidelines when participating in these forums. The collective knowledge and support found in these online spaces can significantly enhance your self-directed learning journey.

Career Progression and Opportunities

A strong understanding of analytic geometry, combined with related mathematical and analytical skills, can open doors to a variety of career paths across numerous industries. While there may not be many job titles that explicitly say "Analytic Geometer," the principles are foundational to roles that involve problem-solving, modeling, data analysis, and design. Career progression often depends on further education, specialization, and the development of complementary skills, such as programming or expertise in a specific application domain.

The ability to think spatially, translate real-world problems into mathematical models, and use algebraic techniques for analysis is highly valued by employers. As technology continues to advance, particularly in areas like data science, artificial intelligence, and engineering, the demand for individuals with strong mathematical foundations, including those provided by analytic geometry, is expected to remain robust.

For those exploring potential careers, it's encouraging to know that mathematical skills are transferable and applicable in diverse settings. If you are considering different career paths, reviewing resources on OpenCourser, such as browsing by career development topics, can provide additional insights.

Entry-Level Technical Roles

Graduates with a solid grounding in analytic geometry and related mathematics often find entry-level technical roles in fields like engineering, computer science, data analysis, and finance. In engineering, positions such as junior engineer, design assistant, or CAD technician may utilize these skills for tasks involving drafting, modeling, and basic structural analysis. For example, an entry-level role in civil engineering might involve using CAD software (which relies on analytic geometry) to help design road layouts or drainage systems.

In the tech industry, roles like junior software developer, quality assurance (QA) tester (especially for graphics-intensive applications or games), or entry-level data analyst can benefit from geometric understanding. A junior game developer might work on implementing basic game physics or object interactions which involve coordinate systems and collision detection. An entry-level data analyst might use graphing techniques, rooted in coordinate geometry, to visualize data trends and relationships.

Other areas include roles as an actuarial assistant, where understanding graphs and modeling is important, or in surveying and cartography, where mapping and spatial data are central. These entry-level positions often provide opportunities to apply foundational knowledge while learning more specialized skills on the job or through further training and certifications. A bachelor's degree in mathematics, engineering, computer science, or a related field is typically required for these roles.

Advanced Research Positions

For those with advanced degrees (Master's or Ph.D.) and a deep specialization in areas that build upon analytic geometry, opportunities in research positions become available. These roles are often found in academia (universities and research institutes), government laboratories, and private sector R&D departments. Mathematicians in these roles might conduct fundamental research in fields like algebraic geometry, differential geometry, or topology, pushing the boundaries of mathematical knowledge.

In applied fields, researchers might work on developing new algorithms for computer graphics, computational geometry, robotics, or scientific visualization. For example, a research scientist in computer vision might develop new techniques for 3D reconstruction from images, heavily relying on projective geometry and multi-view analytic geometry. Physicists in research positions often use advanced geometric concepts in theoretical physics, such as modeling spacetime in general relativity or exploring string theory.

These positions typically require a strong publication record, the ability to secure research funding, and expertise in highly specialized mathematical tools and theories. The work is often interdisciplinary, involving collaboration with scientists and engineers from other fields. The path to an advanced research position is rigorous, demanding a significant commitment to education and original scholarly contribution.

This book covers advanced topics that are more aligned with the kind of geometry encountered in research settings.

Cross-Industry Skill Transferability

One of the significant advantages of developing strong skills in analytic geometry and broader mathematics is the high degree of skill transferability across various industries. The core competencies honed through studying analytic geometry—such as logical reasoning, problem-solving, abstract thinking, precision, and the ability to model complex situations—are in high demand in virtually every sector.

An individual with a background in mathematics, including analytic geometry, might start their career in engineering design but later transition into data science by leveraging their analytical and modeling skills. Similarly, skills developed in quantitative finance, which often involves geometric interpretations of data and risk models, can be applicable to operations research or business analytics in other industries. The ability to understand and work with spatial data, a key aspect of analytic geometry, is valuable in fields ranging from urban planning and environmental science to logistics and supply chain management.

Programming skills, often developed alongside mathematical studies (especially when using tools for computation or visualization), further enhance this transferability. The capacity to learn new domain-specific knowledge, combined with a robust mathematical toolkit, allows professionals to adapt to evolving job markets and explore diverse career opportunities throughout their professional lives. This adaptability is a crucial asset in a rapidly changing technological landscape.

For those considering a career change or wanting to understand how their skills might apply elsewhere, resources on general professional development can be quite useful.

Emerging Specialization Areas

As technology evolves, new specialization areas are emerging where skills rooted in analytic geometry and related mathematical disciplines are becoming increasingly crucial. The field of data science and big data analytics, for example, often involves visualizing high-dimensional data and understanding its geometric structure. Techniques like Principal Component Analysis (PCA) have strong geometric interpretations related to projections and coordinate transformations. Machine learning, a subset of artificial intelligence, heavily relies on mathematical concepts, including geometry, for developing and understanding algorithms (e.g., support vector machines have a clear geometric interpretation).

Robotics and autonomous systems represent another burgeoning field. Designing robots that can navigate complex environments, manipulate objects, and interact with the physical world requires sophisticated geometric modeling, path planning algorithms, and sensor data interpretation—all of which draw upon analytic geometry. Similarly, the growth of virtual reality (VR) and augmented reality (AR) technologies demands advanced skills in 3D computer graphics, real-time rendering, and spatial tracking, areas deeply connected to analytic geometry.

Computational biology and bioinformatics are also increasingly using geometric methods to model molecular structures, analyze protein folding, and understand biological systems. Even fields like financial technology (FinTech) are exploring new mathematical models, some of which may have geometric underpinnings, for risk assessment, algorithmic trading, and fraud detection. Staying abreast of these emerging areas can provide opportunities for those with strong mathematical and geometric skills to contribute to cutting-edge innovations.

Challenges and Common Pitfalls

While learning analytic geometry can be a rewarding experience, students and practitioners often encounter certain challenges and common pitfalls. Being aware of these potential hurdles can help in navigating the learning process more effectively and developing a deeper, more robust understanding of the subject.

Addressing these challenges often involves a combination of consistent practice, seeking clarification when needed, and employing different learning strategies to suit individual needs. Remember, finding a subject challenging is a normal part of the learning process, and overcoming these difficulties can lead to greater mastery.

Abstract Visualization Difficulties

One of the primary challenges many learners face with analytic geometry, especially when transitioning from 2D to 3D concepts, is abstract visualization. While 2D coordinate geometry can be readily drawn and visualized on paper or a screen, mentally picturing and manipulating lines, planes, curves, and surfaces in three-dimensional space can be significantly more difficult. Equations that describe these 3D objects, such as Ax + By + Cz + D = 0 for a plane, or equations for spheres, cylinders, and quadric surfaces, may seem abstract without a strong ability to visualize their geometric counterparts.

This difficulty can impede understanding of concepts like the orientation of planes, the intersection of surfaces, or the nature of space curves. Students might struggle to connect the algebraic manipulations of equations with their geometric meaning. For instance, understanding how different parameters in an equation affect the shape, size, or orientation of a 3D object requires a good mental model.

To overcome this, actively using graphing tools (like GeoGebra or plotting libraries in Python) can be immensely helpful. Creating physical models, even simple ones with wires or cardboard, can also aid visualization. Working through many examples and trying to sketch the geometric situations, even if imperfectly, can gradually build spatial reasoning skills. Practice is key to developing the ability to "see" the geometry behind the algebra.

Computational Complexity Management

As problems in analytic geometry become more complex, especially those involving multiple variables, systems of equations, or intricate geometric configurations, the computational complexity can become a significant hurdle. Solving systems of equations to find intersection points of curves or surfaces, performing coordinate transformations involving trigonometric functions, or optimizing distances and angles can lead to lengthy and error-prone algebraic manipulations.

Students might get bogged down in the algebra and lose sight of the underlying geometric problem they are trying to solve. Errors in calculation are common and can lead to incorrect conclusions. Moreover, without efficient strategies, the sheer volume of computation can be discouraging. This is particularly true in advanced topics or real-world applications where "neat" numbers are rare and precision is important.

Developing strong algebraic skills, including careful organization of work and systematic checking, is essential. Learning to use tools like Computer Algebra Systems (CAS) for symbolic manipulation or numerical software for computation can also be beneficial, not as a crutch, but as a way to manage complexity and focus on the conceptual aspects. Understanding when an exact symbolic solution is needed versus when a numerical approximation is sufficient is also an important skill in managing computational demands.

These solution manuals or books with worked examples can be helpful for understanding how to manage computational steps in solving problems.

Bridging Theory-Practice Gaps

Another common challenge is bridging the gap between the theoretical concepts of analytic geometry and their practical application in real-world problems or other disciplines. Students might understand the formulas for distance, slope, or equations of conic sections in an abstract mathematical context but struggle to see how these tools can be used to model a physical situation, design a component, or interpret data.

For example, knowing the equation of a parabola is one thing; recognizing that the cable of a suspension bridge or the path of a projectile can be modeled by a parabola and then using that model to solve a practical problem requires an additional conceptual leap. This gap can make the subject feel disconnected from tangible outcomes, potentially reducing motivation.

To address this, actively seeking out and working through applied problems is crucial. Textbooks and online resources often provide examples from physics, engineering, computer graphics, and other fields. Engaging in project-based learning, as mentioned earlier, is an excellent way to see theory in action. Furthermore, understanding the "why" behind a particular concept or formula—how it was derived and what geometric or physical reality it represents—can make it less of an abstract rule to memorize and more of a tool with a clear purpose.

Common Misconceptions

Several common misconceptions can hinder understanding in analytic geometry. One is confusing the slope of a line with the line itself, or misunderstanding the meaning of a zero or undefined slope. Another is incorrectly applying formulas, such as using the 2D distance formula in a 3D context or mixing up the standard equations for different conic sections. Students might also struggle with the concept that an equation represents a geometric object—that every point on the object satisfies the equation and every point satisfying the equation is on the object.

Misinterpretations of algebraic results in a geometric context are also frequent. For example, finding no real solutions to a system of equations might correctly mean that two curves do not intersect, but students might mistakenly assume they made an algebraic error. Confusing variables and constants, or misunderstanding the role of parameters in an equation, can also lead to errors. For instance, in the equation of a circle (x-h)² + (y-k)² = r², understanding that h, k, and r are parameters defining a specific circle, while x and y are variables representing the coordinates of any point on that circle, is crucial.

Careful attention to definitions, consistent practice with a variety of problems, and explicitly addressing these potential points of confusion can help to overcome such misconceptions. Drawing diagrams to visualize the problem and checking the reasonableness of algebraic results against geometric intuition are good habits to develop.

Interdisciplinary Connections

Analytic geometry does not exist in a vacuum. It forms crucial connections with various other branches of mathematics and serves as a foundational tool for numerous scientific and technological fields. Recognizing these interdisciplinary links can deepen one's appreciation for the power and versatility of analytic geometry and highlight its role in the broader landscape of human knowledge.

These connections often mean that advancements in one area can spur progress in another, creating a dynamic interplay of ideas and techniques. For students and professionals alike, understanding these relationships can open up new avenues for learning and application.

Exploring these connections might lead you to related fields. For instance, Data Science and Artificial Intelligence are rapidly growing areas with strong mathematical underpinnings.

Links to Linear Algebra and Calculus

Analytic geometry has profound and bidirectional links with both linear algebra and calculus. Linear algebra, which deals with vector spaces, matrices, and linear transformations, can be seen as a generalization and formalization of many concepts first encountered in 2D and 3D analytic geometry. [yfqjj3] Vectors, equations of lines and planes, and systems of linear equations are all fundamental topics in both fields. Coordinate transformations (translation, rotation, scaling) in analytic geometry are elegantly represented and manipulated using matrices in linear algebra.

Calculus, the study of change, relies heavily on the framework provided by analytic geometry. [bbgvsp, 9qdcuj, 29] Concepts like functions, graphs, limits, derivatives (representing slopes of tangent lines to curves), and integrals (representing areas under curves or volumes of solids) are typically introduced and developed within a Cartesian coordinate system. Multivariable calculus, in particular, is almost entirely built upon 3D analytic geometry, dealing with partial derivatives, vector calculus (gradient, divergence, curl), and multiple integrals over regions and surfaces defined in space. [y2x0t0] Analytic geometry provides the stage upon which the drama of calculus unfolds.

Conversely, tools from linear algebra and calculus can be used to solve more complex problems in analytic geometry. For instance, calculus can be used to find tangents and normals to complex curves, or to determine properties like curvature. [iehrm9] Linear algebra provides powerful methods for analyzing systems of equations that might arise from the intersection of multiple geometric objects.

Applications in Machine Learning

While not always immediately obvious, concepts from analytic geometry and its related fields (like linear algebra) play a significant role in machine learning (ML), a subfield of artificial intelligence. Many ML algorithms operate on data that can be thought of as points in a high-dimensional space. For example, if you have a dataset where each item has 'n' features, each item can be represented as a vector (or point) in an n-dimensional space.

Geometric concepts like distance and similarity are crucial. Algorithms like k-Nearest Neighbors (k-NN) classify new data points based on the 'distance' to their neighbors in the feature space. Support Vector Machines (SVMs) aim to find an optimal hyperplane that best separates data points belonging to different classes in a high-dimensional space; this is inherently a geometric problem. Dimensionality reduction techniques, such as Principal Component Analysis (PCA), have strong geometric interpretations, involving projecting data onto lower-dimensional subspaces while preserving as much variance as possible—a concept related to coordinate transformations and projections.

Understanding the geometry of data and the geometric behavior of algorithms can provide valuable insights into why certain ML models work, how they might fail, and how they can be improved. Fields like topological data analysis also bring more advanced geometric ideas to bear on understanding the "shape" of data.

Geographic Information Systems (GIS)

Geographic Information Systems (GIS) are powerful tools used for capturing, storing, analyzing, managing, and presenting spatial or geographic data. Analytic geometry is absolutely fundamental to GIS. At its core, GIS represents real-world features (like roads, buildings, rivers, or administrative boundaries) as geometric objects—points, lines, and polygons—within a defined coordinate system. The location of these features on the Earth's surface is specified using geographic coordinates (latitude and longitude) which are then often projected onto a 2D planar coordinate system for mapping and analysis.

Analytic geometry provides the mathematical basis for many GIS operations. Calculating distances between locations, finding areas of regions, determining if a point lies within a polygon (e.g., is a specific address within a flood zone?), finding the intersection or union of different geographic layers, and creating buffers around features (e.g., all areas within 1 kilometer of a school) all involve geometric computations based on coordinates and equations.

Furthermore, GIS involves transformations between different map projections and coordinate systems, a direct application of coordinate transformation principles from analytic geometry. The ability to accurately model and analyze spatial relationships is critical for applications in urban planning, environmental management, resource allocation, disaster response, navigation, and many other fields that rely on geographic data.

Quantum Computing Foundations

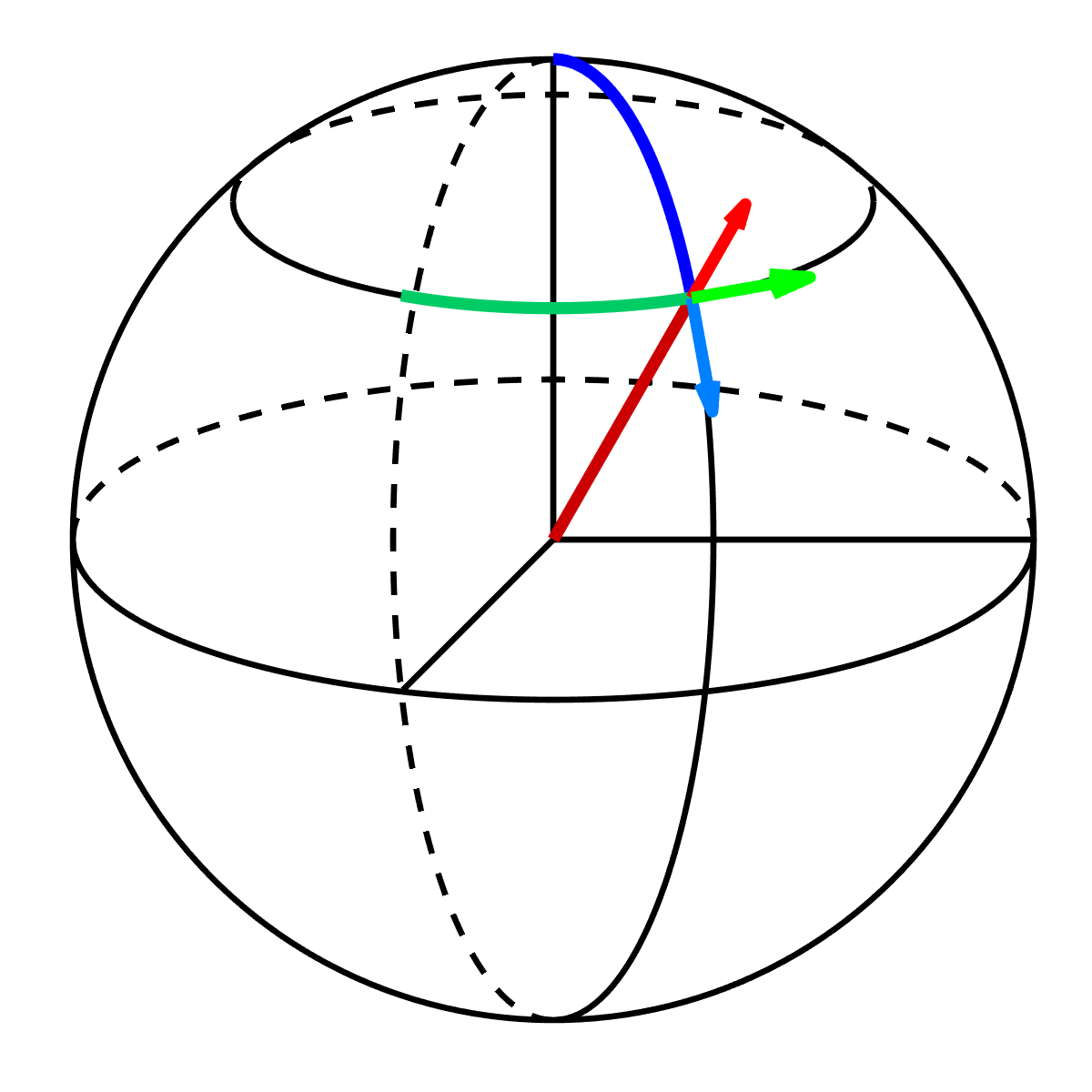
While a more nascent connection, some foundational concepts in quantum computing have links to geometric and algebraic structures where analytic geometry plays a background role, primarily through its extension into linear algebra and complex vector spaces. Quantum bits, or qubits, the basic unit of quantum information, can be represented as vectors in a two-dimensional complex Hilbert space (a type of vector space). The state of a qubit can be visualized on the Bloch sphere, a geometric representation where points on the surface of a sphere correspond to pure quantum states.

Quantum operations, or gates, are represented by unitary matrices that act on these state vectors, effectively performing rotations on the Bloch sphere. Understanding these transformations and the geometry of the state space is important for designing quantum algorithms and understanding quantum phenomena like superposition and entanglement.

While quantum computing itself is a highly specialized field rooted deeply in quantum mechanics and advanced linear algebra, the ability to think in terms of vector spaces, transformations, and geometric representations—skills initially cultivated through analytic geometry—can provide a conceptual bridge to understanding some of its mathematical underpinnings. As quantum computing evolves, the role of geometric and algebraic methods in describing and manipulating quantum states is likely to remain significant.

Frequently Asked Questions (Career Focus)

For those considering how a background in analytic geometry might translate into career opportunities, several questions often arise. This section aims to address some of these common queries, focusing on the practical aspects of leveraging these mathematical skills in the job market.

It's worth noting that while "Analytic Geometer" isn't a common job title, the analytical thinking, problem-solving abilities, and quantitative skills developed through studying this subject are highly valued across many professions. According to the U.S. Bureau of Labor Statistics, overall employment of mathematicians and statisticians is projected to grow significantly faster than the average for all occupations. For instance, one report projects 11% growth from 2023 to 2033. Another source indicates a projected 30% growth for mathematicians and statisticians from 2022 to 2032. These figures underscore the strong demand for mathematical skills.

What are the essential skills for analytic geometry related roles?

Beyond a strong understanding of core analytic geometry concepts (coordinate systems, equations of lines and curves, vectors, transformations), several complementary skills are essential for roles that leverage this knowledge. Strong analytical and problem-solving skills are paramount – the ability to break down complex problems, identify relevant geometric or algebraic approaches, and execute solutions logically. Proficiency in algebra and trigonometry is foundational.

In today's tech-driven world, programming skills are increasingly important. Familiarity with languages like Python, MATLAB, R, or C++ can be crucial for implementing geometric algorithms, performing simulations, or analyzing data. Experience with mathematical software (like GeoGebra, Mathematica, or Maple) or CAD tools can also be beneficial, depending on the specific role.

Good communication skills, both written and verbal, are often underestimated but vital for explaining complex technical concepts to colleagues or clients who may not have a mathematical background. Attention to detail and precision are critical, as small errors in calculation or modeling can have significant consequences. Finally, the ability to learn continuously and adapt to new technologies and methodologies is key, as many fields applying these skills are constantly evolving.

Which industries have the highest demand for these skills?

Skills related to analytic geometry find high demand across a diverse range of industries. The technology sector is a major employer, particularly in areas like software development (especially for graphics, gaming, and simulation), data science, and artificial intelligence/machine learning. Engineering disciplines—including aerospace, mechanical, civil, and electrical—consistently require professionals who can apply geometric principles to design, analysis, and manufacturing.

The finance and insurance industries also seek individuals with strong mathematical and analytical skills for roles such as actuaries, quantitative analysts ("quants"), and risk managers, where modeling and data analysis are key. Government agencies and defense contractors employ mathematicians and engineers for research, development, and operational roles, including areas like cryptography, logistics, and systems analysis.

Furthermore, fields like architecture and urban planning utilize geometric concepts for design and spatial analysis. The rapidly growing field of Geographic Information Systems (GIS) relies heavily on coordinate geometry and spatial analysis skills. Education, both at the secondary and higher education levels, also requires individuals qualified to teach mathematics, including analytic geometry. The demand for these skills reflects the increasing reliance on data-driven decision-making and technological solutions across the economy.

What are some common career advancement certifications?

While there isn't a specific "analytic geometry certification," career advancement often comes through broader certifications relevant to the industry or role one is in, or through advanced degrees. For instance, in engineering, obtaining a Professional Engineer (PE) license is a major career milestone. In finance, certifications like the Chartered Financial Analyst (CFA) or Financial Risk Manager (FRM) can be valuable. Actuaries pursue a rigorous series of exams to achieve Associate or Fellow status in actuarial societies (e.g., Society of Actuaries, Casualty Actuarial Society).

In the technology sector, certifications related to specific software, programming languages, cloud platforms, or data science methodologies (e.g., SAS certifications, Google Professional Data Engineer, AWS Certified Machine Learning) can enhance career prospects. For those in project management roles across various industries, a Project Management Professional (PMP) certification is widely recognized.

Often, more than specific certifications, career advancement in mathematically intensive fields relies on demonstrating a track record of successful problem-solving, innovation, leadership, and continued learning, possibly through advanced degrees (Master's or Ph.D.) which themselves represent a high level of specialized knowledge and research capability. Staying updated with industry trends and new technologies is also crucial. For those looking to save on learning resources, checking for offers on OpenCourser Deals can be beneficial.

Are there freelance or consulting opportunities?

Yes, individuals with strong skills in analytic geometry and related mathematical modeling, programming, and data analysis can find freelance or consulting opportunities. These opportunities often arise in niche areas where specialized expertise is required for short-term projects or specific problem-solving tasks. For example, a company developing a new piece of software with complex graphical components might hire a freelance consultant with expertise in computational geometry or graphics algorithms.

Small to medium-sized engineering firms might seek consultants for specialized design analysis or simulation work. Startups in fields like robotics, AI, or data analytics may also engage consultants for their mathematical modeling or algorithm development needs. Furthermore, there are opportunities for freelance work in technical writing (creating documentation for mathematical software or concepts), curriculum development for educational institutions, or private tutoring and coaching in mathematics.

To succeed as a freelancer or consultant, it's important to build a strong portfolio of projects, develop a professional network, and effectively market your skills. Platforms that connect freelancers with clients can be useful, as can direct outreach to companies in relevant industries. Strong communication and project management skills are also essential for managing client relationships and delivering successful outcomes independently.

How is Artificial Intelligence (AI) impacting the field and related careers?

Artificial Intelligence (AI) is having a multifaceted impact on mathematics and careers that rely on mathematical skills, including those related to analytic geometry. On one hand, AI tools, particularly machine learning, are increasingly being used to assist mathematicians in research, helping to formulate new conjectures, verify proofs, and find patterns in complex data. This can augment the capabilities of mathematicians and potentially accelerate discovery.

On the other hand, AI and automation may also reshape job roles. Some routine tasks involving data analysis or calculation might become more automated, leading to a shift in the skills required. However, the demand for individuals who can develop, understand, and critically evaluate AI models—many of which are built on mathematical foundations—is growing. There is a strong need for professionals who can bridge the gap between mathematical theory and AI application. Fields like AI ethics and AI safety also require deep analytical thinking.

Rather than replacing mathematicians, AI is more likely to become a powerful tool that changes how they work, requiring them to adapt and develop new skills, such as familiarity with machine learning methods and programming. The fundamental ability to think logically, solve problems, and understand abstract concepts—all honed by studying subjects like analytic geometry—will remain highly valuable in an AI-driven world. In fact, a strong math foundation is seen as increasingly important for those looking to work in AI and data science.

What are the international job prospects like?

Job prospects for individuals with strong mathematical skills, including those derived from the study of analytic geometry, are generally global. Mathematics is a universal language, and the principles of analytic geometry are applied worldwide in science, engineering, technology, and finance. Many multinational corporations in these sectors have operations and R&D centers in various countries, creating international employment opportunities.

Developed countries with strong technology and research sectors often have a high demand for mathematicians, statisticians, data scientists, and engineers. Emerging economies are also increasingly investing in STEM education and industries, leading to growing opportunities. Academic and research positions at universities and international research institutions are, by their nature, often globally recruited.

However, international job prospects can be influenced by factors such as visa requirements, language proficiency, recognition of foreign qualifications, and local economic conditions. Certain regions may have a higher concentration of specific industries (e.g., finance in London or New York, tech in Silicon Valley or Bangalore). Professionals seeking international careers should research target countries and industries, network internationally, and be prepared for potential challenges related to relocation and cultural adjustment. Online job boards, professional organizations with international chapters, and university career services can be valuable resources for exploring global opportunities.

Useful Links and Further Exploration

To continue your journey into the world of analytic geometry and related fields, several resources can provide further information, learning opportunities, and insights into career paths.

For those seeking structured learning, exploring online course catalogs is a great starting point. OpenCourser provides a vast library of courses across various subjects.

• Mathematics Courses on OpenCourser: Discover a wide range of mathematics courses, from foundational to advanced levels.
• OpenCourser Learner's Guide: Find articles and tips on how to make the most of online learning, structure your studies, and achieve your educational goals.
• U.S. Bureau of Labor Statistics - Mathematicians and Statisticians: Explore detailed information about the job outlook, pay, and educational requirements for careers in mathematics and statistics.
• Khan Academy - Analytic Geometry: Access free lessons and practice exercises on various topics within analytic geometry.

These resources offer a blend of learning materials, career information, and tools to support your exploration of analytic geometry and its many applications. Whether you are a student, a professional looking to upskill, or simply a curious learner, the journey into this fascinating branch of mathematics is rich with discovery.

Analytic geometry, with its elegant blend of algebra and geometry, serves as a critical underpinning for much of modern science, technology, and engineering. Its principles allow us to model the world around us with precision, from the microscopic to the cosmic, and to develop innovative solutions to complex problems. Whether your path leads to a career directly involving mathematical research or one that applies these foundational concepts in other domains, a solid understanding of analytic geometry provides a powerful intellectual toolkit and a unique perspective on the interconnectedness of mathematical ideas and their real-world impact.