Hypothesis Testing
Hypothesis Testing: A Comprehensive Guide
Hypothesis testing is a cornerstone of statistical analysis, providing a structured framework for making decisions and drawing conclusions from data. At its core, it's a method used to determine whether there is enough evidence in a sample of data to infer that a certain condition is true for an entire population. Imagine a company claiming their new website design increases user engagement; hypothesis testing offers a formal process to assess whether any observed increase is a genuine improvement or simply due to random chance. This process is fundamental in a vast array of fields, enabling researchers, analysts, and decision-makers to move beyond intuition and base their conclusions on statistical evidence.
The power of hypothesis testing lies in its ability to bring scientific rigor to problem-solving. Whether you're a medical researcher evaluating the efficacy of a new drug, a marketing analyst assessing the impact of an advertising campaign, or a quality control engineer monitoring production processes, hypothesis testing provides the tools to make informed judgments. It’s an exciting field because it allows you to uncover insights hidden within data, challenge existing assumptions, and contribute to evidence-based advancements. The ability to formulate and test hypotheses effectively is a highly valued skill, opening doors to numerous analytical and research-oriented career paths.
Introduction to Hypothesis Testing
This section will introduce you to the fundamental ideas behind hypothesis testing, its purpose, core components, and its wide-ranging applications. Understanding these basics is the first step toward appreciating the power and utility of this statistical method.
What is Hypothesis Testing and Why Is It Important?
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is a statistical method used to determine if there's enough evidence in sample data to draw conclusions about a larger population. Essentially, it's a way to test an assumption or theory to see if it's supported by the evidence. For example, a scientist might hypothesize that a new fertilizer increases crop yield, or a business might assume a new marketing strategy will boost sales. Hypothesis testing provides a structured way to evaluate these claims.
The primary purpose of hypothesis testing is to make a decision between two competing statements or hypotheses about a population parameter. This decision-making process is crucial because it helps to distinguish between random variation and a genuine effect or difference. Without a formal testing procedure, we might incorrectly attribute chance occurrences to real phenomena or, conversely, miss important discoveries.
The importance of hypothesis testing spans numerous disciplines. In scientific research, it’s fundamental for validating theories and making new discoveries. In business, it informs strategic decisions, such as whether to launch a new product or implement a new operational process, by allowing professionals to test theories before committing significant resources. In healthcare, it's used to determine the effectiveness of new treatments or interventions. Ultimately, hypothesis testing provides a systematic and objective approach to decision-making in the face of uncertainty.
These courses offer a solid introduction to the core ideas of hypothesis testing, suitable for those new to the field.
Core Components of Hypothesis Testing
To understand hypothesis testing, one must become familiar with its key components. These elements form the building blocks of any hypothesis test and guide the entire process from question formulation to conclusion.
The first crucial components are the null hypothesis (H₀) and the alternative hypothesis (H₁ or Ha). The null hypothesis typically represents a statement of no effect or no difference; it's the default assumption. For instance, H₀ might state that a new drug has no effect on recovery time. The alternative hypothesis is what you are trying to find evidence for; it's a statement that contradicts the null hypothesis. It might state that the new drug does affect recovery time (either by decreasing or increasing it, or simply by being different).
Another key concept is the p-value. The p-value is the probability of observing data as extreme as, or more extreme than, what was actually observed, assuming the null hypothesis is true. A small p-value suggests that the observed data is unlikely if the null hypothesis were true, thus providing evidence against the null hypothesis. This leads to the concept of the significance level (alpha, α), which is a pre-determined threshold (commonly 0.05, or 5%). If the p-value is less than or equal to alpha, the result is considered statistically significant, and we reject the null hypothesis in favor of the alternative hypothesis.
Think of it like a courtroom trial. The null hypothesis is like the defendant being presumed innocent (no effect). The alternative hypothesis is the prosecutor's claim that the defendant is guilty (there is an effect). The data collected is the evidence presented. The p-value is like an assessment of how surprising the evidence would be if the defendant were truly innocent. If the evidence is very surprising (a very small p-value), the jury (the researcher) might reject the presumption of innocence (the null hypothesis) and conclude guilt (support the alternative hypothesis).
Understanding these components is foundational for anyone looking to apply statistical methods rigorously.
Real-World Impact of Hypothesis Testing
Hypothesis testing is not just an academic exercise; it has profound real-world applications that impact daily life and major societal advancements. Its principles are applied across a diverse range of fields to make critical decisions and drive innovation.
In research, hypothesis testing is the bedrock of the scientific method. Scientists use it to test theories about everything from the behavior of subatomic particles to the effects of climate change. For example, an ecologist might test the hypothesis that a certain pollutant is affecting fish populations in a river, or a psychologist might test whether a new therapy technique is more effective than an existing one.
In healthcare and medicine, hypothesis testing is indispensable. Clinical trials, which evaluate the safety and efficacy of new drugs and medical treatments, rely heavily on hypothesis testing to determine if a new treatment is genuinely better than a placebo or an existing standard treatment. Epidemiologists use hypothesis testing to identify risk factors for diseases and to evaluate the effectiveness of public health interventions. For example, testing whether a vaccine reduces the incidence of a disease is a classic application.
In the business world, hypothesis testing helps companies make data-driven decisions to improve products, services, and marketing strategies. A company might use A/B testing (a form of hypothesis testing) to determine which version of a webpage leads to more conversions, or whether a new advertising campaign results in a significant increase in sales. Financial analysts might test hypotheses about stock market trends or the performance of investment strategies. This systematic approach allows businesses to minimize risks and optimize outcomes by verifying assumptions before large-scale implementation.
These courses provide insights into how hypothesis testing is applied in practical, real-world business contexts.
If you're keen on exploring various statistical concepts further, OpenCourser offers a wide selection of courses within Data Science and Mathematics.
Understanding Hypotheses and Testing Frameworks
Delving deeper into hypothesis testing requires a clear understanding of the different types of hypotheses that can be formulated and the various frameworks available for testing them. This knowledge is crucial for selecting the appropriate methodology for a given research question or problem.
The Foundation: Null and Alternative Hypotheses
As introduced earlier, the null hypothesis (H₀) and the alternative hypothesis (H₁ or Ha) are the two competing statements that a hypothesis test evaluates. The null hypothesis is a statement of no effect, no difference, or no relationship between variables. It often reflects a prevailing belief or a baseline assumption that the researcher seeks to challenge. For example, in a study comparing two teaching methods, the null hypothesis might state that there is no difference in student performance between the two methods.
The alternative hypothesis, on the other hand, is a statement that contradicts the null hypothesis. It posits that there is an effect, a difference, or a relationship. It represents what the researcher is trying to demonstrate. Continuing the teaching method example, the alternative hypothesis might state that there is a difference in student performance, or more specifically, that one method is superior to the other. These two hypotheses must be mutually exclusive, meaning that if one is true, the other must be false, and together they should cover all possible outcomes.
Formulating clear and precise null and alternative hypotheses is the critical first step in hypothesis testing. The nature of these hypotheses dictates the type of test to be used and how the results will be interpreted. A poorly formulated hypothesis can lead to ambiguous or incorrect conclusions, undermining the entire research effort.
These resources can help you solidify your understanding of how to frame null and alternative hypotheses.
Guiding the Test: Directional and Non-Directional Hypotheses
Alternative hypotheses can be further classified as either directional (one-tailed) or non-directional (two-tailed). This distinction is important because it affects the critical region of the statistical test and, consequently, how the p-value is calculated and interpreted.
A directional hypothesis (one-tailed test) specifies the direction of the expected difference or relationship. For example, a researcher might hypothesize that a new drug increases reaction time, or that a specific marketing campaign leads to a decrease in customer churn. In these cases, the researcher is interested in an effect in only one specific direction. The critical region for a one-tailed test is located entirely in one tail (either left or right) of the sampling distribution of the test statistic.
Conversely, a non-directional hypothesis (two-tailed test) states that there is a difference or relationship, but does not specify the direction. For instance, the hypothesis might be that a new website design has an effect on user engagement, without predicting whether engagement will increase or decrease. Here, the researcher is interested in detecting a significant difference in either direction. The critical region for a two-tailed test is split between both tails of the sampling distribution.
Choosing between a one-tailed and a two-tailed test depends on the research question and any prior knowledge or strong theoretical reasons to expect an effect in a particular direction. Generally, two-tailed tests are more conservative because they require stronger evidence to reject the null hypothesis, as the significance level (alpha) is divided between the two tails.
This course delves into the nuances of different types of tests, including directional aspects.
Choosing Your Tools: Parametric vs. Non-Parametric Tests
Once hypotheses are formulated, the next step involves selecting an appropriate statistical test. Tests are broadly categorized into parametric and non-parametric tests, and the choice depends heavily on the assumptions made about the data, particularly the distribution of the population from which the sample is drawn, and the type of data being analyzed (e.g., continuous, categorical).
Parametric tests assume that the data are drawn from a population that follows a specific distribution, often a normal distribution. They also typically require that the data be measured on an interval or ratio scale. Common examples of parametric tests include the t-test (used to compare means of one or two groups), Analysis of Variance (ANOVA) (used to compare means of three or more groups), and Pearson correlation. When their assumptions are met, parametric tests are generally more powerful than non-parametric tests, meaning they are more likely to detect a significant effect if one truly exists.
Non-parametric tests, also known as distribution-free tests, make fewer assumptions about the population distribution. They are often used when the assumptions of parametric tests are violated (e.g., data are not normally distributed, sample sizes are small) or when dealing with ordinal or nominal data. Examples include the Mann-Whitney U test (non-parametric alternative to the independent samples t-test), Wilcoxon signed-rank test (non-parametric alternative to the paired t-test), Kruskal-Wallis test (non-parametric alternative to ANOVA), and the Chi-square test (used to analyze categorical data).
Selecting the correct type of test is critical for the validity of the results. Using a parametric test when its assumptions are not met can lead to misleading conclusions. Conversely, using a non-parametric test when a parametric test is appropriate might result in a loss of statistical power. Therefore, understanding the characteristics of your data and the assumptions of different statistical tests is essential for sound hypothesis testing.
The following courses cover various statistical tests, including both parametric and non-parametric approaches.
For those interested in the broader field of statistical methods, these books offer comprehensive coverage.
The Hypothesis Testing Process: A Step-by-Step Approach
Hypothesis testing follows a logical sequence of steps, ensuring that the process is systematic and the conclusions are defensible. While the specifics may vary slightly depending on the test used, the general framework remains consistent. Mastering this workflow is key to conducting sound statistical analyses.
Setting the Stage: Formulating Your Hypotheses
The very first step in any hypothesis test is to clearly define the research question and then translate it into statistical hypotheses: the null hypothesis (H₀) and the alternative hypothesis (H₁ or Ha). As discussed earlier, H₀ typically represents the status quo or a statement of no effect, while H₁ represents what the researcher aims to find evidence for.
For example, if a pharmaceutical company develops a new drug to lower blood pressure, the research question is: "Does the new drug effectively lower blood pressure?" The hypotheses would be:
- H₀: The new drug has no effect on blood pressure (or μ_drug = μ_placebo, where μ is the average blood pressure).
- H₁: The new drug lowers blood pressure (a one-tailed test, e.g., μ_drug < μ_placebo), or the new drug affects blood pressure (a two-tailed test, e.g., μ_drug ≠ μ_placebo).
The hypotheses must be stated precisely and in terms of population parameters before any data is collected or analyzed. This ensures objectivity and prevents the research question from being influenced by the observed data. This initial step sets the entire direction for the subsequent analysis.
This course provides a focused look at formulating effective hypotheses.
Making Critical Choices: Significance Levels and Test Statistics
After formulating the hypotheses, the next crucial step involves selecting a significance level (α). The significance level is the probability of making a Type I error, which is rejecting the null hypothesis when it is actually true. Commonly used values for α are 0.05 (5%), 0.01 (1%), or 0.10 (10%). The choice of α depends on the context of the research and the consequences of making a Type I error. A lower α means that stronger evidence is required to reject H₀.
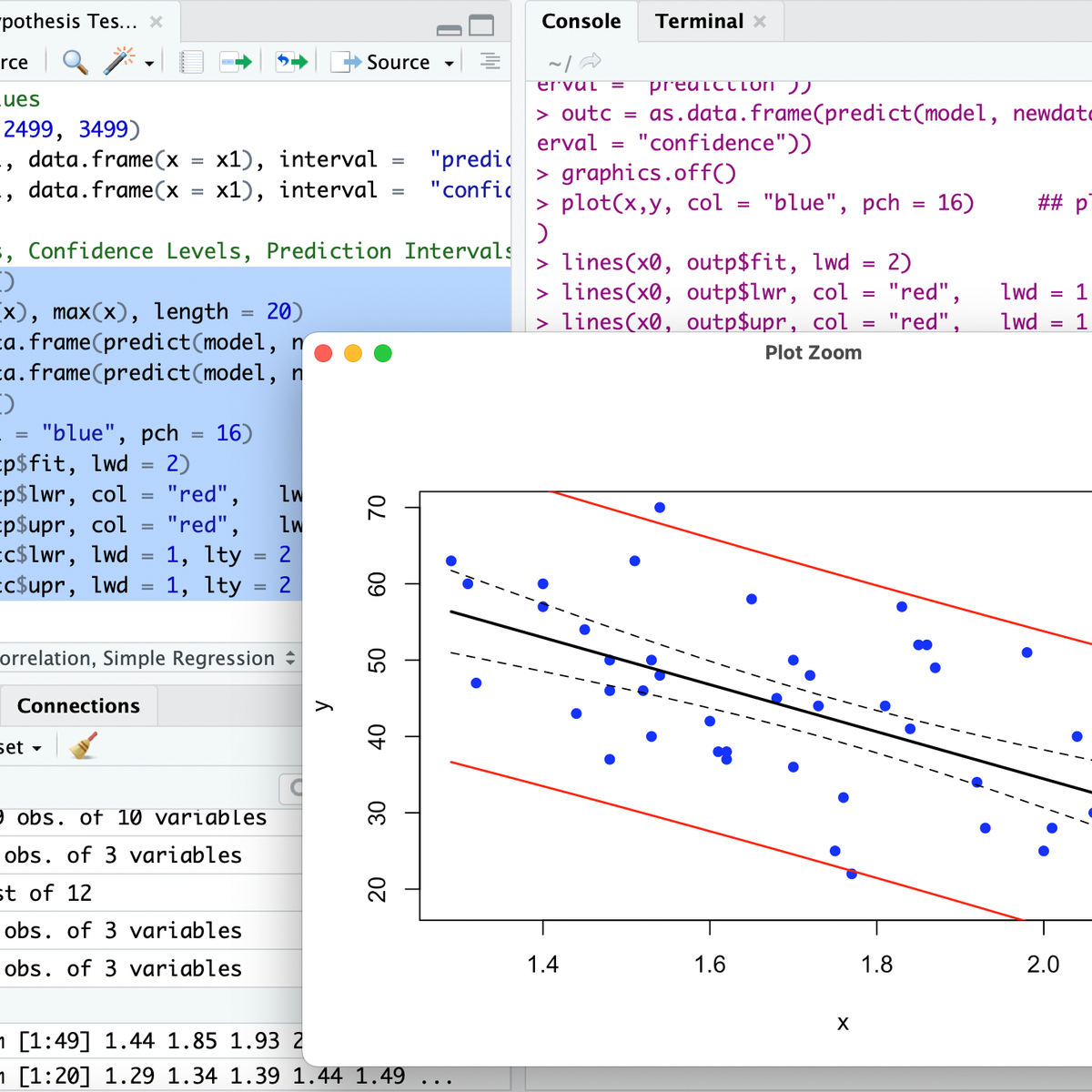
Following this, an appropriate test statistic must be chosen. The test statistic is a value calculated from the sample data that measures how far the sample estimate of the parameter is from the value stated in the null hypothesis. The choice of test statistic depends on several factors, including the type of data, the sample size, whether the population standard deviation is known, and the specific hypotheses being tested. Common test statistics include the z-statistic, t-statistic, F-statistic, and chi-square statistic.
An analysis plan should also be formulated at this stage. This plan outlines how the data will be collected and analyzed. It includes defining the population of interest, the sampling method, the sample size, and the specific statistical test that will be used. A well-thought-out plan ensures that the data collected will be appropriate for testing the hypotheses and that the chosen statistical methods are valid.
The courses below cover the selection of significance levels and appropriate test statistics.
Interpreting the Evidence: P-Values and Drawing Sound Conclusions
Once the data are collected and the test statistic is calculated, the next step is to determine the p-value associated with that test statistic. The p-value quantifies the evidence against the null hypothesis. It represents the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed, assuming H₀ is true.
To make a decision, the p-value is compared to the pre-determined significance level (α).
- If p-value ≤ α: We reject the null hypothesis (H₀). This means there is statistically significant evidence to support the alternative hypothesis (H₁).
- If p-value > α: We fail to reject the null hypothesis (H₀). This means there is not enough statistically significant evidence to support the alternative hypothesis. It's important to note that failing to reject H₀ does not mean H₀ is true; it simply means the data did not provide sufficient evidence to reject it.
Finally, a conclusion is drawn in the context of the original research question. This involves interpreting the statistical decision in practical terms. For instance, if H₀ (new drug has no effect) is rejected, the conclusion might be that the new drug is effective in lowering blood pressure. The conclusion should also acknowledge any limitations of the study and suggest areas for future research. Clear communication of the results, including the hypotheses, methods, p-value, and conclusion, is paramount for transparency and reproducibility.
These courses focus on the critical skills of interpreting p-values and drawing valid conclusions.
Understanding the process is one thing, but grasping the interpretation of results is another. Consider these books for deeper insights.
Navigating Common Challenges in Hypothesis Testing
While hypothesis testing is a powerful tool, it's not without its pitfalls. Researchers and analysts must be aware of common challenges and misinterpretations to ensure the integrity and validity of their findings. Addressing these issues is crucial for maintaining statistical literacy and ethical research practices.
Understanding Errors and Power in Statistical Tests
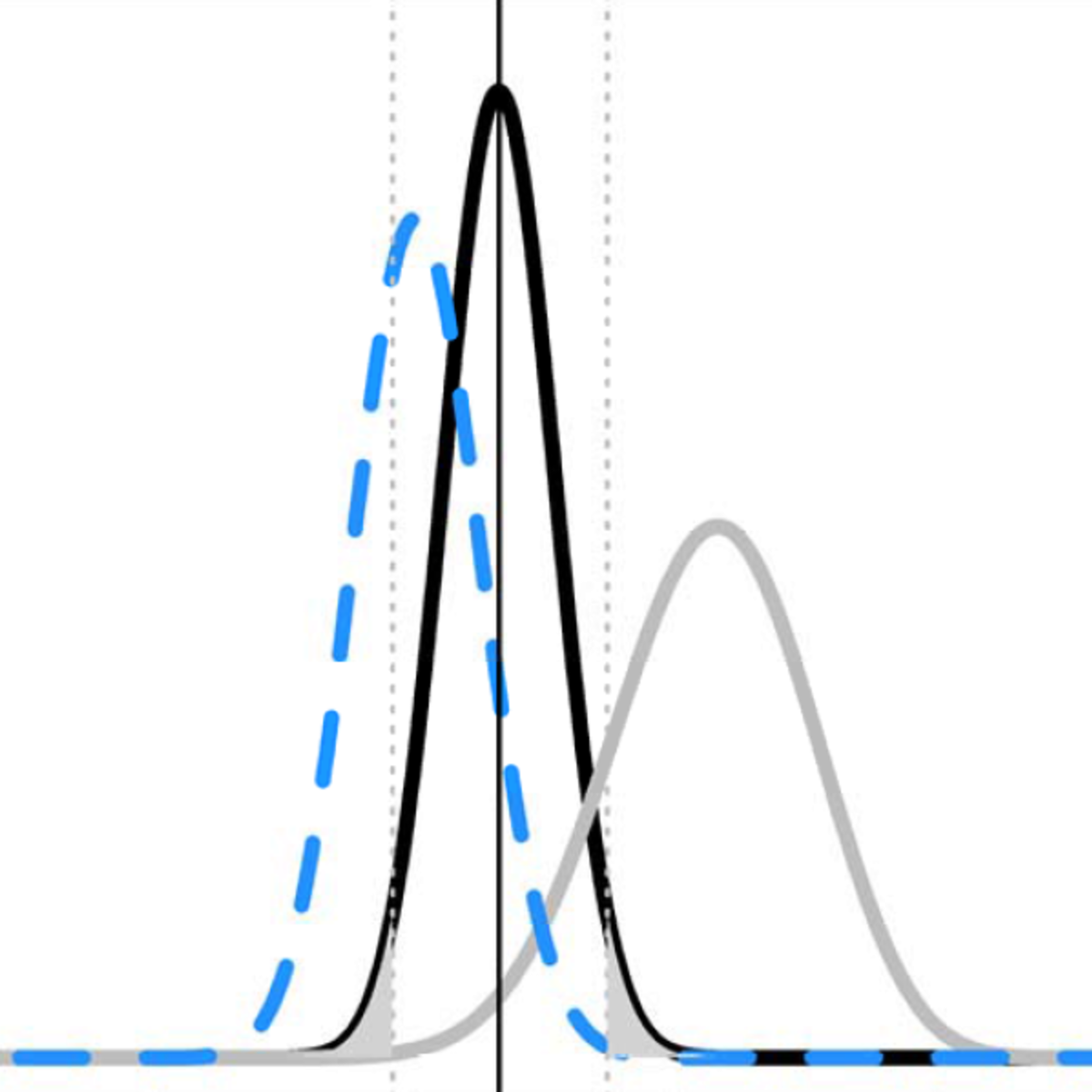
In hypothesis testing, decisions are made based on probabilities, meaning there's always a chance of making an incorrect decision. Two types of errors can occur: Type I error and Type II error.
A Type I error occurs when we reject a true null hypothesis. This is also known as a "false positive." The probability of committing a Type I error is denoted by alpha (α), the significance level we choose for the test. For example, if α = 0.05, there's a 5% chance of incorrectly concluding there's an effect when, in reality, there isn't one.
A Type II error occurs when we fail to reject a false null hypothesis. This is also known as a "false negative." The probability of committing a Type II error is denoted by beta (β). This means we fail to detect an effect that actually exists. The complement of beta (1 - β) is known as the statistical power of a test. Power is the probability that the test will correctly reject a false null hypothesis (i.e., detect an effect when it's there).
Imagine a medical test for a disease. A Type I error would be telling a healthy person they have the disease (false positive). A Type II error would be telling a sick person they are healthy (false negative). There's often a trade-off: reducing the chance of a Type I error (e.g., by lowering α) can increase the chance of a Type II error, and vice versa, assuming other factors like sample size remain constant. Researchers strive to design studies with sufficient power to detect meaningful effects while controlling the Type I error rate at an acceptable level.
These courses help in understanding the critical concepts of statistical errors and power.
For a more detailed read on statistical power, consider this book.
Avoiding Deceptive Practices: P-Hacking and Data Dredging
The pressure to publish significant results can sometimes lead to questionable research practices, such as p-hacking and data dredging. These practices can distort findings and contribute to the irreproducibility of research.
P-hacking (or p-value hacking) refers to the practice of trying multiple statistical analyses or data manipulation techniques until a statistically significant p-value (typically p < 0.05) is found. This might involve selectively reporting results, trying different statistical tests, excluding certain outliers, or stopping data collection when a significant result is achieved. P-hacking inflates the rate of false positives because it essentially "cherry-picks" significant results from what might be a series of non-significant analyses conducted on the same dataset.
Data dredging (also known as data fishing or significance chasing) is a broader term that involves extensively analyzing large datasets to find any statistically significant patterns or relationships, often without pre-specified hypotheses. While exploratory data analysis is valuable, presenting findings from data dredging as if they were confirmatory (i.e., testing pre-specified hypotheses) is misleading. Such findings are more likely to be spurious due to the sheer number of comparisons made.
Both p-hacking and data dredging undermine the scientific process by producing results that appear statistically significant but are likely due to chance and are often not replicable. Transparency in research methods, pre-registration of studies (stating hypotheses and analysis plans before data collection), and a focus on replication are key strategies to combat these deceptive practices.
Beyond P-Values: The Importance of Effect Sizes
While p-values indicate statistical significance (i.e., whether an effect is likely not due to chance), they do not convey the magnitude or practical importance of the effect. A very small p-value can be obtained for a trivial effect if the sample size is extremely large. This is where effect sizes become crucial.
Effect size is a quantitative measure of the magnitude of a phenomenon. It could be the difference between two group means, the correlation between two variables, or the risk reduction due to an intervention. For example, if a new teaching method results in a statistically significant improvement in test scores (p < 0.05), the effect size would tell us how much of an improvement was observed (e.g., an average increase of 2 points vs. 20 points on a 100-point scale). A small effect size, even if statistically significant, might not be practically meaningful or warrant changes in policy or practice.
Reporting and interpreting effect sizes alongside p-values provides a more complete picture of the research findings. It helps researchers and practitioners assess the real-world relevance of an observed effect. Many scientific journals now encourage or require the reporting of effect sizes to move beyond a binary focus on statistical significance and promote a more nuanced understanding of research results.
To understand the nuances of statistical reporting beyond just p-values, this course can be beneficial.
OpenCourser's Learner's Guide offers valuable articles on how to approach complex topics like these and structure your learning effectively.
Hypothesis Testing in the Age of Machine Learning
Hypothesis testing, a traditional cornerstone of statistical inference, continues to play a vital role in the modern field of machine learning (ML). While the goals and some methodologies differ, the fundamental principles of formulating and testing assumptions against data remain relevant and valuable for building robust and interpretable ML models.
Ensuring Model Quality: A/B Testing for Validation
A/B testing, a common application of hypothesis testing, is widely used in machine learning to compare the performance of different models or model versions. For instance, if a data science team develops a new recommendation algorithm (Model B) intended to replace an existing one (Model A), A/B testing can be employed to determine if Model B genuinely performs better on key metrics like click-through rate or conversion rate.
In this scenario, the null hypothesis would typically state that there is no difference in performance between Model A and Model B. The alternative hypothesis would state that Model B performs better (or differently, for a two-tailed test). By randomly assigning users or requests to either Model A or Model B and collecting performance data, a statistical test can be conducted to see if the observed differences are statistically significant or likely due to random chance.
This rigorous approach to model validation helps in making data-driven decisions about deploying new models, ensuring that changes lead to actual improvements and avoiding the premature rollout of models that might perform worse or no better than existing ones. It's a crucial step in the iterative process of model development and refinement.
This course offers practical insights into A/B testing, a key hypothesis testing application in tech.
Smart Feature Selection Through Hypotheses
Feature selection is a critical step in building effective machine learning models. Including irrelevant or redundant features can lead to overfitting, increased computational cost, and reduced model interpretability. Hypothesis testing can aid in a more principled approach to feature selection.
For each potential feature, one can formulate a hypothesis. The null hypothesis might state that the feature has no relationship with the target variable (e.g., its coefficient in a regression model is zero, or it provides no information gain in a decision tree). The alternative hypothesis would state that the feature does have a relationship with the target variable.
Statistical tests (like t-tests for regression coefficients, chi-square tests for categorical features, or ANOVA for comparing means across feature groups) can then be used to assess the significance of each feature. Features for which the null hypothesis is not rejected (i.e., those with high p-values) may be considered candidates for removal. This hypothesis-driven approach helps ensure that only statistically relevant features are included in the final model, potentially leading to better generalization and performance.
The following courses touch upon data analysis and feature relevance, which are related to hypothesis-driven feature selection.
Bringing Clarity to Complexity: Statistical Interpretation of Black-Box Models
Many advanced machine learning models, such as deep neural networks or complex ensemble methods, are often referred to as "black-box" models because their internal workings can be difficult to interpret directly. While these models can achieve high predictive accuracy, understanding why they make certain predictions is crucial for trust, debugging, and ensuring fairness.
Hypothesis testing can contribute to the interpretability of these models. For example, permutation importance techniques assess feature importance by randomly shuffling the values of a single feature and observing the drop in model performance. One could formulate a null hypothesis that a feature has no importance (i.e., shuffling its values does not significantly decrease performance). Statistical tests can then evaluate this hypothesis.
Furthermore, techniques like LIME (Local Interpretable Model-agnostic Explanations) or SHAP (SHapley Additive exPlanations) provide insights into individual predictions. While not direct hypothesis tests in the traditional sense, the underlying principles of assessing the contribution of different factors (features) to an outcome resonate with the exploratory nature often associated with generating hypotheses for further investigation. Statistical methods can help determine if the explanations provided by these tools are stable and reliable.
These resources delve into statistical methods relevant to machine learning and model evaluation.
Career Opportunities with Hypothesis Testing Skills
A strong grasp of hypothesis testing is a valuable asset in a wide array of professions. The ability to formulate testable questions, design experiments, analyze data rigorously, and draw statistically sound conclusions is highly sought after by employers across numerous industries. If you're exploring career paths or looking to transition, developing expertise in hypothesis testing can open up exciting opportunities.
Exploring Roles That Utilize Hypothesis Testing
Many roles inherently involve hypothesis testing as a core component of their responsibilities. For instance, a Biostatistician in the pharmaceutical or public health sector designs clinical trials and analyzes data to test the efficacy and safety of new drugs or interventions. Their work directly impacts patient care and public health policies. The job outlook for statisticians, including biostatisticians, is strong, with the U.S. Bureau of Labor Statistics (BLS) projecting significant growth in this field.
A Marketing Analyst uses hypothesis testing to evaluate the effectiveness of marketing campaigns, website designs (through A/B testing), pricing strategies, and customer segmentation. They help businesses understand consumer behavior and optimize marketing spend for better returns. Similarly, a UX Researcher formulates hypotheses about user behavior and tests them through usability studies, surveys, and experiments to improve product design and user experience.
Other roles where hypothesis testing is crucial include Data Scientists, who build and evaluate predictive models; Economists, who test economic theories and policy impacts; Quality Assurance Engineers, who test whether products meet certain specifications; and Environmental Scientists, who test hypotheses about environmental changes and the impact of pollutants. Even in fields like Psychology and Social Sciences, researchers rely heavily on hypothesis testing to advance knowledge.
Here are some careers that heavily utilize hypothesis testing skills:
Understanding Compensation in Hypothesis Testing Careers
Salaries for roles that require hypothesis testing skills vary significantly based on factors such as industry, geographic location, years of experience, level of education, and the specific responsibilities of the position. However, given the demand for analytical skills, these roles generally offer competitive compensation.
For example, according to the U.S. Bureau of Labor Statistics (BLS), the median annual wage for statisticians was $104,110 in May 2023. The BLS also projects robust job growth for statisticians, with an anticipated 30% increase in employment from 2022 to 2032, which is much faster than the average for all occupations. Data from the BLS Occupational Outlook Handbook provides detailed information on salary ranges and job growth for related professions such as Data Scientists, Operations Research Analysts, and Market Research Analysts, all of whom employ hypothesis testing.
Roles like Data Scientist and Biostatistician, particularly those requiring advanced degrees (Master's or Ph.D.) and specialized expertise, often command higher salaries. Even entry-level positions that involve data analysis and hypothesis testing can offer a solid starting salary with good prospects for growth as skills and experience develop. Staying updated with industry benchmarks and salary surveys from reputable sources can provide a more precise understanding of compensation expectations in your specific area of interest.
These courses can help build foundational knowledge often required for roles with strong earning potential.
Showcasing Your Abilities: Portfolio Projects
For those seeking to enter or advance in careers involving hypothesis testing, a strong portfolio of projects is an excellent way to demonstrate practical expertise to potential employers. Theoretical knowledge is important, but showcasing your ability to apply these concepts to real-world (or realistic) problems can set you apart.
Portfolio projects can take many forms. You might analyze a publicly available dataset to answer a specific research question, conducting a full hypothesis test from formulation to conclusion. For instance, you could test if there's a significant difference in housing prices between two neighborhoods, or if a particular social media activity correlates with user engagement metrics. Clearly document your process: the hypotheses, data cleaning steps, chosen statistical test and why, the results (including p-values and effect sizes), and your interpretation.
Another idea is to replicate a published study (giving proper credit, of course) or conduct an A/B test on a personal website or a simulated scenario. If you're learning R or Python, use these tools for your analysis and share your code on platforms like GitHub. Contributing to open-source data analysis projects or participating in data science competitions can also provide valuable project experience. Remember, the goal is to show not just that you know the definitions, but that you can think statistically and solve problems using data.
Building a strong portfolio can be a journey. Starting with foundational courses can give you the skills needed to tackle interesting projects.
Consider exploring books that offer case studies or practical examples to inspire your projects.
Pathways to Mastering Hypothesis Testing
Developing expertise in hypothesis testing is a journey that can be approached through various educational avenues. Whether you are a student looking to build foundational knowledge or a professional aiming to upskill, there are numerous resources available to help you master the concepts and tools of hypothesis testing.
Formal Education vs. Online Learning for Hypothesis Testing
Traditional university programs, particularly in statistics, mathematics, data science, economics, psychology, and other research-intensive fields, provide a structured and comprehensive education in hypothesis testing. These programs typically offer in-depth theoretical understanding, hands-on practice with statistical software, and opportunities for research projects or theses. A bachelor's, master's, or even a Ph.D. can provide a strong credential for careers requiring advanced statistical expertise.
In parallel, the rise of online learning has made statistical education, including hypothesis testing, more accessible than ever. Numerous online courses and certifications are available, ranging from introductory modules to specialized advanced topics. Platforms like OpenCourser aggregate a vast number of such courses, allowing learners to find options that fit their schedule, budget, and learning style. Online courses can be an excellent way to supplement formal education, acquire specific skills (like proficiency in R or Python for statistical analysis), or make a career transition. Many online programs now offer rigorous curricula and recognized credentials. For those looking to save on course fees, checking OpenCourser Deals can be a great way to find discounts on relevant courses.
Ultimately, the choice between formal education and online learning, or a combination of both, depends on individual career goals, existing knowledge, available resources, and learning preferences. Both pathways can effectively equip you with the necessary skills in hypothesis testing.
Here are some online courses that offer comprehensive learning in statistics and hypothesis testing, suitable for various levels.
Essential Tools for Hypothesis Testing: R and Python
Proficiency in statistical software is almost indispensable for anyone serious about applying hypothesis testing in practice. While various software packages exist (like SPSS, SAS, Minitab), R and Python have become two of the most popular open-source tools in the data analysis and data science communities.
R is a programming language and free software environment specifically designed for statistical computing and graphics. It has an extensive ecosystem of packages (libraries) that provide functions for a vast array of statistical tests, data manipulation, and visualization. R is widely used in academia and by statisticians for its powerful statistical capabilities and active community support.
Python, a versatile general-purpose programming language, has also gained immense popularity in data science thanks to powerful libraries like NumPy (for numerical computing), Pandas (for data manipulation and analysis), SciPy (which includes a statistics module with many hypothesis tests), and Statsmodels (for more advanced statistical modeling). Python's ease of learning and integration with other data science workflows (like machine learning) make it an attractive choice.
Learning one or both of these languages will significantly enhance your ability to conduct hypothesis tests, manage complex datasets, and automate analytical workflows. Many online courses specifically focus on teaching statistics using R or Python, providing practical, hands-on experience.
These courses can help you get started with R and Python for statistical analysis.
Learning by Doing: Real-World Case Studies
Theoretical knowledge of hypothesis testing concepts is crucial, but the ability to apply these concepts to real-world problems is what truly builds expertise. Engaging with case studies is an excellent way to bridge the gap between theory and practice.
Case studies present a scenario or problem, often with an accompanying dataset, and challenge you to apply statistical methods, including hypothesis testing, to arrive at a solution or conclusion. They allow you to see how different tests are chosen and applied in specific contexts, how results are interpreted, and what challenges can arise in real-world data analysis (e.g., missing data, outliers, violated assumptions).
Many textbooks, online courses, and academic journals feature case studies. You can also find public datasets from government agencies, research institutions, or platforms like Kaggle to create your own case studies. Working through these examples, perhaps by trying to replicate the original analysis or by exploring alternative approaches, can significantly deepen your understanding and problem-solving skills. This hands-on experience is invaluable for building confidence and developing the practical intuition needed in any analytical role.
Courses that often include case studies or project-based learning can be highly beneficial.
Books focusing on applications in specific fields often contain rich case studies.
If you're exploring career paths, the Career Development section on OpenCourser might offer additional insights into skill-building strategies.
Ethical Implications in Hypothesis Testing
The power of hypothesis testing to influence decisions in science, policy, and business comes with significant ethical responsibilities. Practitioners must be vigilant about maintaining integrity, objectivity, and transparency throughout the research process to ensure that statistical findings are credible and used responsibly.
Addressing the Reproducibility Challenge in Research
The "reproducibility crisis" or "replication crisis" refers to the growing concern that many findings in scientific research cannot be reliably reproduced by independent researchers. This issue has significant implications for the credibility of science. While hypothesis testing itself is a sound methodology, its misuse or misapplication can contribute to irreproducible results. Factors contributing to this crisis include publication bias (favoring positive or novel results), p-hacking, inadequate statistical power, and lack of transparency in methods and data.
Ethical statistical practice demands a commitment to producing reproducible research. This includes transparently reporting all methodological details, including how hypotheses were formulated, how data were collected and processed, the specific statistical tests used, and the assumptions made. Sharing data and analysis code, where appropriate and ethically permissible, also enhances reproducibility by allowing others to verify the findings. Promoting a research culture that values replication studies and acknowledges null findings is also crucial. Organizations like the Stanford Encyclopedia of Philosophy have documented the complexities and importance of reproducibility in science.
Efforts to address the reproducibility crisis include advocating for open science practices, pre-registration of studies, and more rigorous statistical training. As a practitioner, understanding these issues and committing to best practices is an ethical imperative.
This course touches upon improving the quality and reliability of statistical inferences.
Maintaining Objectivity: Bias in Hypothesis Formulation
Bias can creep into the hypothesis testing process at various stages, but it can be particularly problematic during hypothesis formulation. Researchers may consciously or unconsciously formulate hypotheses in a way that favors a desired outcome or confirms pre-existing beliefs. This can lead to biased data collection, selective reporting of results, or misinterpretation of findings.
For example, if a company funding a study has a vested interest in a particular outcome (e.g., showing their product is superior), there might be pressure to frame hypotheses or interpret results in a way that supports this outcome. Ethical practitioners must guard against such influences and strive for objectivity. This means formulating hypotheses based on sound theory and prior evidence, not on desired results. It also involves being open to results that contradict one's expectations or interests.
Transparency about funding sources, potential conflicts of interest, and the rationale behind hypothesis formulation is essential. Peer review and replication by independent researchers can also help to identify and mitigate the impact of bias. Ultimately, the goal is to ensure that conclusions are driven by the data, not by preconceived notions or external pressures.
For further reading on ethical practices, the American Statistical Association provides comprehensive Ethical Guidelines for Statistical Practice, which emphasize integrity and accountability.
The Importance of Openness: Transparency in Reporting Results
Transparency in reporting the results of hypothesis tests is fundamental to ethical statistical practice. This means providing a full and honest account of the research process, not just the "significant" or favorable findings. Selective reporting, or "cherry-picking," where only statistically significant results are published while non-significant or contradictory findings are suppressed, leads to a distorted view of the evidence and contributes to publication bias.
Ethical reporting includes detailing the sample size and how it was determined, the specific statistical tests used and why they were chosen, the exact p-values (not just whether p < 0.05), effect sizes, and confidence intervals. It's also important to discuss any limitations of the study, assumptions made, and how violations of assumptions were handled. If multiple hypotheses were tested, this should be disclosed, along with any adjustments made for multiple comparisons.
By being transparent, researchers allow others to critically evaluate their work, replicate their findings, and build upon their research. This openness fosters trust in the scientific process and helps to ensure that decisions based on statistical evidence are well-founded. Embracing transparency is a cornerstone of responsible research and a key element in upholding the integrity of statistical practice.
Courses focusing on research methods often cover aspects of ethical reporting.
The Evolving Landscape of Hypothesis Testing
Hypothesis testing, while rooted in classical statistical theory, is not a static field. It continues to evolve in response to technological advancements, new data paradigms, and ongoing methodological debates. Understanding these trends is important for anyone looking to stay at the forefront of data analysis and statistical inference.
The Rise of AI in Statistical Analysis
Artificial Intelligence (AI) and machine learning are increasingly intersecting with traditional statistical methods, including hypothesis testing. AI-driven tools are being developed to automate aspects of the analytical workflow, from data preparation and feature selection to even suggesting or performing hypothesis tests.
For example, AI algorithms can help identify complex patterns in large datasets that might not be apparent through conventional methods, leading to the formulation of new hypotheses. Some platforms aim to make statistical analysis more accessible by allowing users to ask questions in natural language, with AI translating these into formal tests. While automation offers the potential for increased efficiency and the ability to analyze more complex data, it also raises questions about the interpretability of AI-driven conclusions and the need for human oversight to ensure the appropriate application of statistical principles. The future likely involves a synergy where AI augments human analytical capabilities rather than entirely replacing them.
These courses touch upon the intersection of AI, data analysis, and statistical concepts.
Ongoing Debates: Bayesian vs. Frequentist Approaches
The field of statistics has long hosted a philosophical and practical debate between two major schools of thought: frequentist and Bayesian inference. Hypothesis testing, as traditionally taught and widely practiced, is predominantly rooted in the frequentist framework. This framework defines probability as the long-run frequency of events and focuses on controlling error rates (like Type I and Type II errors) over repeated experiments.
Bayesian inference, on the other hand, treats probability as a degree of belief about a hypothesis or parameter. It combines prior beliefs (expressed as a prior probability distribution) with observed data (through a likelihood function) to arrive at an updated belief (a posterior probability distribution). Bayesian hypothesis testing often involves comparing the plausibility of different hypotheses given the data, for example, by calculating Bayes factors. Proponents argue that Bayesian methods offer a more intuitive interpretation of evidence and can better incorporate prior knowledge.
While frequentist methods remain dominant in many fields, Bayesian approaches are gaining traction, particularly with increased computational power that makes their implementation more feasible. The debate is ongoing, and many statisticians see value in both perspectives, suggesting that the choice of approach may depend on the specific research question and context. Understanding the foundations of both can provide a richer toolkit for statistical inference.
This course introduces Bayesian concepts within hypothesis testing.
Further exploration into Statistics can provide deeper insights into these differing paradigms.
Meeting New Demands: Adapting to Big Data and Streaming Analytics
The era of "big data" – characterized by massive volumes, high velocity, and wide variety of data – presents both opportunities and challenges for hypothesis testing. Traditional methods, often designed for smaller, well-structured datasets, may need adaptation to be effective in this new landscape.
With extremely large sample sizes common in big data, even tiny, practically insignificant effects can become statistically significant (i.e., yield very small p-values). This underscores the increased importance of focusing on effect sizes and practical relevance rather than solely on statistical significance. Furthermore, the computational burden of performing tests on massive datasets requires efficient algorithms and distributed computing frameworks.
Streaming analytics, where data arrives continuously and needs to be analyzed in real-time (e.g., sensor data, website traffic, financial transactions), poses unique challenges. Hypothesis tests may need to be adapted to update dynamically as new data comes in, and methods for online error control become crucial. The development of scalable and adaptive statistical methods is an active area of research to ensure that hypothesis testing remains a relevant and powerful tool in the age of big data and real-time information.
These courses address statistical methods suitable for large datasets and modern analytical environments.
Frequently Asked Questions About Careers in Hypothesis Testing
Embarking on or transitioning into a career that utilizes hypothesis testing can raise many practical questions. Here, we address some common queries to help guide your career exploration and planning.
Do I need a PhD to use hypothesis testing in industry roles?
Not necessarily. While a PhD is often required for advanced research positions, academic roles, or roles involving the development of new statistical methodologies, many industry positions that utilize hypothesis testing are accessible with a Bachelor's or Master's degree. Roles like Data Analyst, Marketing Analyst, Business Analyst, or Junior Data Scientist often require a strong understanding of statistical concepts and the ability to apply them, which can be gained through undergraduate or Master's level education, supplemented by practical experience and online certifications. The key is to demonstrate proficiency in applying statistical methods to solve real-world problems, regardless of the specific degree level.
How do I transition from academic to corporate hypothesis testing roles?
Transitioning from academia to corporate roles involves highlighting the transferable skills gained through academic research. Emphasize your experience in formulating hypotheses, designing experiments or studies, collecting and analyzing data, interpreting results, and communicating findings. Tailor your resume to showcase practical applications of your statistical skills and familiarity with industry-relevant tools (like R, Python, SQL, Excel). Networking with professionals in your target industry, gaining experience through internships or freelance projects, and building a portfolio of applied projects can significantly aid this transition. Focus on how your analytical abilities can solve business problems and drive value.
What industries value hypothesis testing skills most in 2024?
Hypothesis testing skills are valued across a wide range of industries. Key sectors include:
- Healthcare and Pharmaceuticals: For clinical trials, epidemiological research, and healthcare analytics.
- Technology and E-commerce: For A/B testing, product development, user experience research, and data science.
- Finance and Insurance: For risk management, fraud detection, algorithmic trading, and actuarial science.
- Marketing and Advertising: For campaign effectiveness analysis, market research, and consumer behavior studies.
- Manufacturing and Engineering: For quality control, process improvement (e.g., Six Sigma), and reliability testing.
- Government and Public Policy: For program evaluation, economic analysis, and social science research.
Can I automate hypothesis testing in my workflow?
Parts of the hypothesis testing workflow can be automated, especially with tools like R and Python. For instance, you can write scripts to perform calculations for test statistics and p-values once the data is prepared and the test is chosen. Some modern analytics platforms and AI tools are also aiming to further automate aspects of hypothesis generation and testing. However, critical steps like formulating meaningful hypotheses, choosing the appropriate test based on data characteristics and assumptions, interpreting the results in context, and understanding the ethical implications still require human judgment and expertise. Automation can aid efficiency, but it doesn't replace the need for sound statistical thinking.
How to explain hypothesis testing concepts in job interviews?
When explaining hypothesis testing in an interview, aim for clarity and conciseness. Start with a simple definition: it's a statistical method to test an assumption or theory about a population using sample data. Briefly explain the null and alternative hypotheses, the p-value, and the significance level. Use a simple, relatable example to illustrate the process (e.g., testing if a new website design increases clicks). Emphasize the decision-making aspect: whether to reject or fail to reject the null hypothesis based on evidence. If possible, relate it to a project you've worked on or a problem relevant to the role you're interviewing for. Highlighting your ability to not just perform the test but also to interpret and communicate the results effectively is key.
What certifications boost employability for hypothesis testing roles?
While specific "hypothesis testing" certifications are rare, certifications in broader fields like Data Science, Business Analytics, Six Sigma (Green Belt, Black Belt), or specialized software (like SAS Certified Statistical Business Analyst) can demonstrate relevant skills. Certifications from reputable university-affiliated online programs or well-known industry training providers can also be valuable. More important than the certification itself is the knowledge and practical skills gained. Ensure any certification program includes hands-on projects and covers the statistical foundations thoroughly. Employers will typically be more interested in your demonstrated ability to apply these skills than in a certificate alone.
The following courses and topics can provide strong foundations or specialized knowledge relevant to careers involving hypothesis testing.
Pursuing a path involving hypothesis testing requires dedication and a willingness to engage with sometimes complex statistical ideas. However, the ability to make sense of data and contribute to evidence-based decisions is an incredibly rewarding and increasingly vital skill in today's world. With the right resources and a commitment to learning, you can certainly develop the expertise needed to thrive in this area. OpenCourser is here to help you browse thousands of courses and find the educational resources that best fit your journey.