Trigonometric Functions
An Introduction to Trigonometric Functions: Understanding Angles and Their Relationships
Trigonometric functions, at their core, are mathematical tools that describe the relationship between the angles and side lengths of triangles. These functions, often referred to as circular functions, are fundamental not just in pure mathematics but across a wide array of scientific and technical disciplines. While they might initially seem like an abstract concept confined to textbooks, trigonometric functions are the unsung heroes behind many everyday technologies and scientific advancements. Understanding them opens a door to comprehending the geometric underpinnings of the world around us.
The study of these functions primarily revolves around right-angled triangles, where one angle is 90 degrees. The most common trigonometric functions are sine (sin), cosine (cos), and tangent (tan), along with their reciprocals: cosecant (csc), secant (sec), and cotangent (cot). These functions allow us to calculate unknown angles or distances when other measurements are known. Imagine being able to determine the height of a tall building without directly measuring it, or calculating the vast distances between celestial bodies – these are tasks made possible by the power of trigonometric functions. Their periodic nature, meaning their values repeat in regular intervals, also makes them indispensable for analyzing wave phenomena, such as sound and light waves.
What Are Trigonometric Functions?
At a foundational level, trigonometric functions are ratios of the lengths of the sides of a right-angled triangle. For any given acute angle in a right triangle, these ratios remain constant, regardless of the size of the triangle. This consistency is what makes trigonometric functions so powerful and universally applicable.
The primary trigonometric functions are:
- Sine (sin): For an acute angle in a right triangle, the sine of that angle is the ratio of the length of the side opposite the angle to the length of the hypotenuse (the side opposite the right angle).
- Cosine (cos): The cosine of an acute angle is the ratio of the length of the adjacent side (the side next to the angle, which is not the hypotenuse) to the length of the hypotenuse.
- Tangent (tan): The tangent of an acute angle is the ratio of the length of the side opposite the angle to the length of the adjacent side.
Beyond these, there are three reciprocal functions:
- Cosecant (csc): The reciprocal of sine (1/sin).
- Secant (sec): The reciprocal of cosine (1/cos).
- Cotangent (cot): The reciprocal of tangent (1/tan).
These definitions, initially tied to acute angles in right triangles, can be extended to angles of any magnitude using the concept of the unit circle – a circle with a radius of one centered at the origin of a coordinate plane. This broader definition allows for the analysis of periodic phenomena and a wider range of applications.
These books offer comprehensive introductions and deeper dives into the world of trigonometry.
Historical Development of Trigonometric Functions
The journey of trigonometric functions is a fascinating story that spans millennia and cultures, driven by humanity's enduring curiosity about the cosmos and the practical needs of measurement and navigation. The earliest roots of studying angles and ratios can be traced back to ancient Egyptian and Babylonian mathematics. These civilizations laid groundwork in geometry and angle measurement, with Sumerian astronomers, for instance, dividing the circle into 360 degrees.
Contributions from Ancient Greek, Indian, and Islamic Mathematicians
The systematic study of trigonometric functions truly began in the Hellenistic world during the 3rd century BC. Greek mathematicians, notably Hipparchus of Nicaea (circa 190–120 BCE), are credited with pioneering this field. Hipparchus is often called "the father of trigonometry" for compiling the first known table of chords, which are closely related to the sine function. He focused on relating arcs of a circle to the lengths of the chords they subtend, primarily for astronomical calculations. Later, Ptolemy (circa 100–170 CE) in his influential work, the Almagest, further developed these concepts, providing methods to calculate the motions of celestial bodies using elementary spherical trigonometry.
The knowledge then traveled to India, where it flourished, especially during the Gupta period (4th to 6th centuries CE). Indian mathematicians like Aryabhata (6th century CE) made significant strides, developing tables for sine (which he called "jya"), cosine, and versine. These advancements were crucial for astronomical computations and demonstrate a shift towards the function-based understanding we use today.
During the Islamic Golden Age (roughly 8th to 14th centuries), the study of trigonometry was further refined and expanded. Mathematicians such as Muhammad ibn Mūsā al-Khwārizmī (early 9th century) produced accurate sine and cosine tables and contributed to spherical trigonometry. Habash al-Hasib al-Marwazi (circa 830 CE) is credited with discovering the tangent and cotangent. Al-Battānī (Albatenius) (853–929 CE) discovered the secant and cosecant. Notably, Naṣīr al-Dīn al-Ṭūsī (1201–1274) was among the first to treat trigonometry as a distinct mathematical discipline, separate from astronomy.
Development During the Renaissance and Modern Era
The knowledge of trigonometric functions reached Europe through translations of Arabic and Greek texts, particularly during the Renaissance. Regiomontanus (Johannes Müller von Königsberg, 1436–1476) authored De triangulis omnimodis (On Triangles of Every Kind) around 1464 (published in 1533), which was the first modern book devoted entirely to trigonometry and was particularly strong on the sine function. The term "trigonometry" itself first appeared in a book titled Trigonometria by Bartholomeo Pitiscus in 1595.
The development of modern trigonometry accelerated during the Age of Enlightenment. Mathematicians like Isaac Newton and James Stirling in the 17th century, and later Leonhard Euler in the 18th century, made profound contributions. Euler, in particular, was instrumental in establishing the modern analytical approach to trigonometric functions, introducing the notation we use today (e.g., sin, cos, tan) and discovering fundamental relationships like Euler's formula (eix = cos x + i sin x), which links trigonometric functions with exponential functions.
Impact of Calculus on Trigonometric Analysis
The advent of calculus in the 17th and 18th centuries, developed by Newton and Gottfried Wilhelm Leibniz, had a profound impact on the understanding and application of trigonometric functions. Calculus provided tools to analyze the rates of change and accumulation related to these functions, leading to a deeper understanding of their properties, such as their derivatives and integrals. The derivatives of sine and cosine functions, for instance, exhibit a cyclical pattern that is fundamental to solving differential equations, which model a vast range of physical phenomena.
Furthermore, calculus enabled the development of power series representations for trigonometric functions, allowing for their precise calculation and manipulation. This interplay between calculus and trigonometry paved the way for advanced mathematical theories like Fourier analysis, which decomposes complex periodic functions into sums of simple sine and cosine waves, a technique with immense applications in signal processing, physics, and engineering. The ability to analyze periodic behavior with such precision transformed many scientific and engineering disciplines.
Core Trigonometric Functions and Their Properties
The heart of trigonometry lies in its six core functions: sine (sin), cosine (cos), tangent (tan), and their respective reciprocals, cosecant (csc), secant (sec), and cotangent (cot). These functions form the basis for understanding relationships between angles and side lengths in right-angled triangles and extend to broader applications through the unit circle.
Detailed Analysis of Sine, Cosine, Tangent, and Their Inverses
As previously defined, for an angle θ in a right-angled triangle:
- sin(θ) = Opposite / Hypotenuse
- cos(θ) = Adjacent / Hypotenuse
- tan(θ) = Opposite / Adjacent (which can also be expressed as sin(θ) / cos(θ))
Their reciprocals are:
- csc(θ) = 1 / sin(θ) = Hypotenuse / Opposite
- sec(θ) = 1 / cos(θ) = Hypotenuse / Adjacent
- cot(θ) = 1 / tan(θ) = Adjacent / Opposite (or cos(θ) / sin(θ))
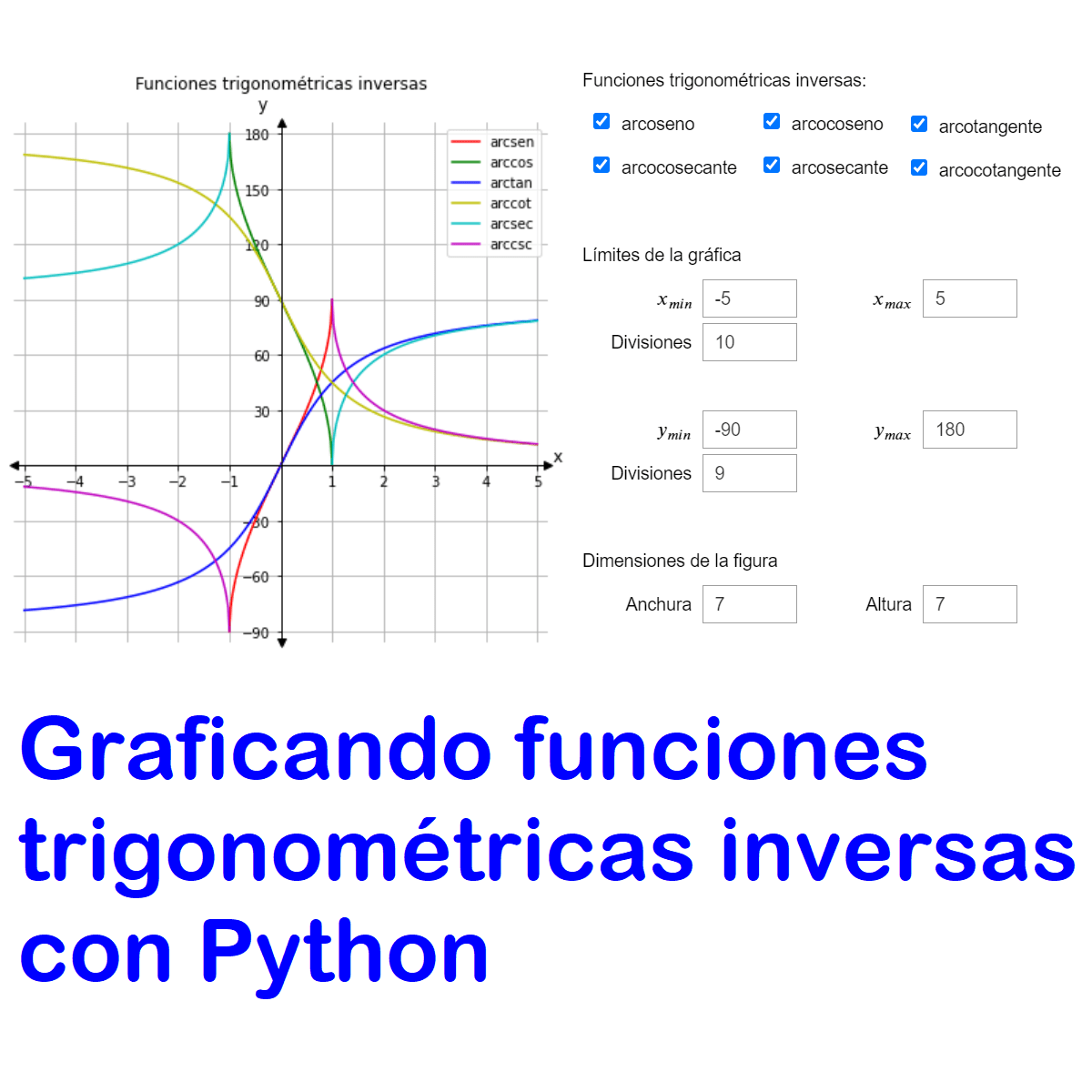
Each of these trigonometric functions has an inverse function. These inverse functions are used to find an angle when the ratio of two sides is known. They are often denoted with "arc" prefix or a superscript "-1" (e.g., arcsin(x) or sin-1(x)). It is crucial to note that sin-1(x) does not mean 1/sin(x); that is csc(x). Instead, sin-1(x) asks: "What angle has a sine of x?". Similar interpretations apply to arccos(x), arctan(x), and the inverses of the other trigonometric functions.
Understanding these functions is a key step in mastering mathematics. These courses provide a structured way to learn about special functions, including trigonometric ones, and how to apply them.
Graphical Representations and Periodic Behavior
When graphed on a coordinate plane, trigonometric functions reveal their characteristic periodic nature.
The sine function (y = sin(x)) produces a smooth, oscillating wave that starts at the origin (0,0), rises to a maximum value of 1 at x = π/2 (90°), passes through zero at x = π (180°), reaches a minimum value of -1 at x = 3π/2 (270°), and returns to zero at x = 2π (360°), completing one full cycle. The period of the sine function is 2π radians (or 360°), meaning the graph repeats itself every 2π interval. The amplitude, which is half the difference between the maximum and minimum values, is 1.
The cosine function (y = cos(x)) is also a smooth, oscillating wave, identical in shape to the sine wave but shifted horizontally. It starts at its maximum value of 1 at x = 0, passes through zero at x = π/2 (90°), reaches its minimum value of -1 at x = π (180°), passes through zero again at x = 3π/2 (270°), and returns to its maximum value of 1 at x = 2π (360°). Like the sine function, its period is 2π radians (or 360°), and its amplitude is 1. In fact, the cosine graph is simply the sine graph shifted to the left by π/2 radians (90°).
The tangent function (y = tan(x)) has a distinctly different graph. It passes through the origin (0,0) and increases towards positive infinity as x approaches π/2 (90°) from the left, and approaches negative infinity as x approaches π/2 from the right. The tangent function has vertical asymptotes at x = π/2, 3π/2, 5π/2, etc. (and their negative counterparts), where the function is undefined. Unlike sine and cosine, the tangent function does not have a maximum or minimum value; its range is all real numbers. The period of the tangent function is π radians (or 180°).
The graphs of the reciprocal functions (cosecant, secant, and cotangent) can be derived from the graphs of sine, cosine, and tangent, respectively. For example, where sin(x) = 0, csc(x) will have a vertical asymptote, and where sin(x) reaches a local maximum or minimum, csc(x) will have a corresponding local minimum or maximum.
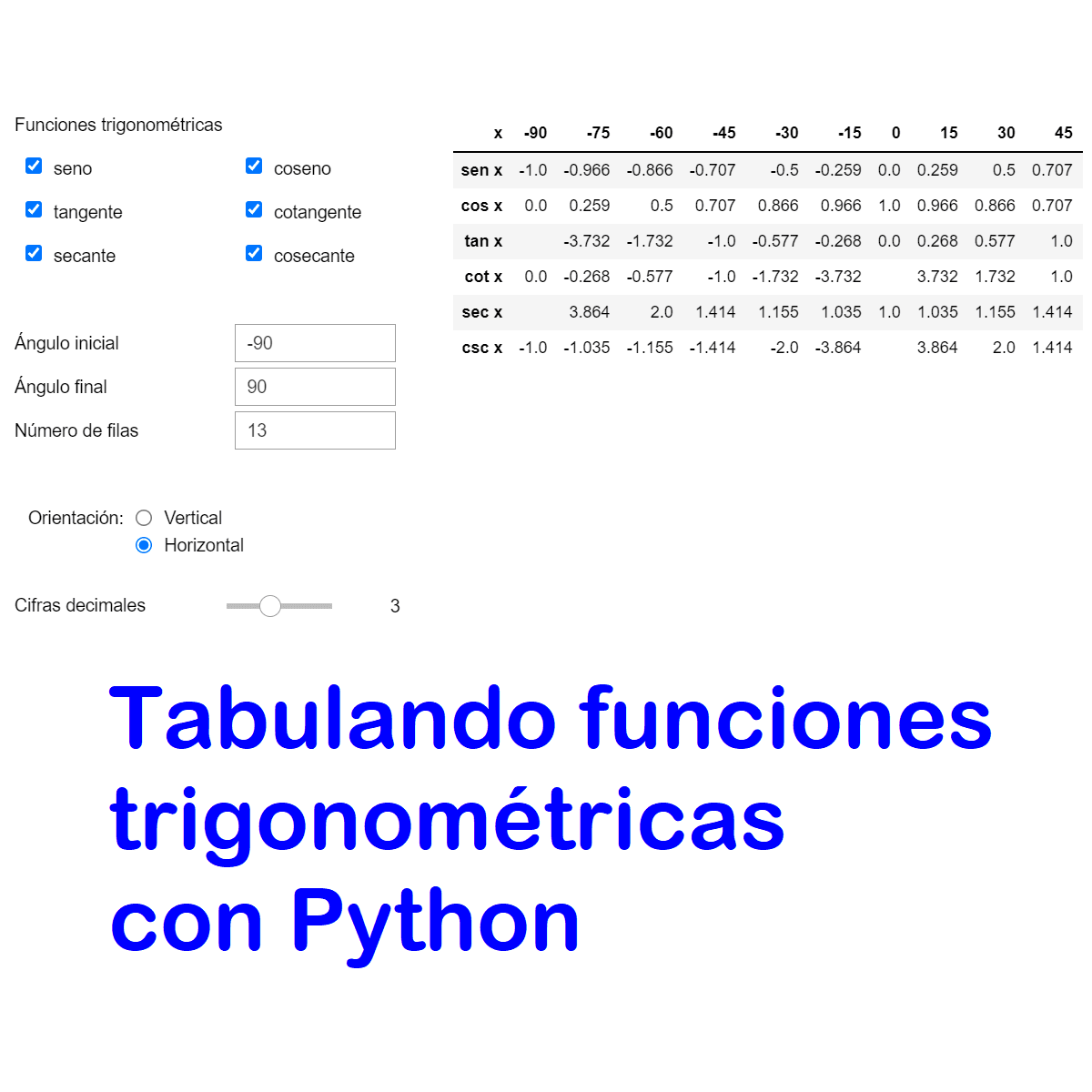
For those interested in how programming can be used to explore these concepts, these courses delve into tabulating and graphing trigonometric functions using Python.
Key Identities (e.g., Pythagorean, Sum/Difference Formulas)
Trigonometric identities are equations involving trigonometric functions that are true for all values of the variables for which both sides of the equation are defined. These identities are incredibly useful for simplifying expressions, solving trigonometric equations, and rewriting expressions in more convenient forms.
Some of the most fundamental identities include:
-
Pythagorean Identities: These are derived from the Pythagorean theorem. The most well-known is:
- sin2(θ) + cos2(θ) = 1
- 1 + tan2(θ) = sec2(θ)
- 1 + cot2(θ) = csc2(θ)
-
Reciprocal Identities: These define the reciprocal functions:
- csc(θ) = 1 / sin(θ)
- sec(θ) = 1 / cos(θ)
- cot(θ) = 1 / tan(θ)
-
Quotient Identities:
- tan(θ) = sin(θ) / cos(θ)
- cot(θ) = cos(θ) / sin(θ)
-
Sum and Difference Formulas (Angle Addition/Subtraction Formulas): These express trigonometric functions of the sum or difference of two angles in terms of the functions of the individual angles. For example:
- sin(α ± β) = sin(α)cos(β) ± cos(α)sin(β)
- cos(α ± β) = cos(α)cos(β) ∓ sin(α)sin(β)
- tan(α ± β) = (tan(α) ± tan(β)) / (1 ∓ tan(α)tan(β))
-
Double-Angle Formulas: These are special cases of the sum formulas where α = β. For example:
- sin(2θ) = 2sin(θ)cos(θ)
- cos(2θ) = cos2(θ) - sin2(θ) = 2cos2(θ) - 1 = 1 - 2sin2(θ)
- tan(2θ) = 2tan(θ) / (1 - tan2(θ))
- Half-Angle Formulas: These express trigonometric functions of half an angle in terms of functions of the original angle.
There are many other identities, including power-reduction formulas, sum-to-product formulas, and product-to-sum formulas. Mastering these identities is essential for advanced work in mathematics, physics, and engineering. They allow for the manipulation of complex trigonometric expressions into simpler or more useful forms.
To deepen your understanding of core trigonometric functions and their identities, consider these resources. "Calculus" provides a foundational understanding, while the "Handbook of Mathematical Functions" is an extensive reference.
Applications of Trigonometric Functions
Trigonometric functions are far more than abstract mathematical concepts; they are indispensable tools with a vast range of practical applications across numerous fields. Their ability to model periodic phenomena and relationships involving angles and distances makes them fundamental to solving real-world problems.
Waveform Analysis in Signal Processing
One of the most significant applications of trigonometric functions, particularly sine and cosine, is in signal processing. Signals, such as sound waves, light waves, radio waves, and electrical signals, often exhibit periodic behavior that can be represented by combinations of sine and cosine functions. This is the core idea behind Fourier analysis, a mathematical technique that allows complex waveforms to be decomposed into a sum of simpler sinusoidal components. Engineers use Fourier analysis and trigonometric functions to analyze, filter, and manipulate signals. For example, in audio processing, these tools help in noise reduction, equalization, and sound synthesis. In telecommunications, they are crucial for modulating and demodulating signals, enabling the transmission of information over various media. The very music you listen to on a computer can be developed using sine or cosine functions to model sound waves.
These courses delve into Fourier analysis, a key area where trigonometric functions are heavily applied in signal processing.
Structural Engineering and Force Calculations
In civil and structural engineering, trigonometry is essential for designing stable and safe structures like bridges, buildings, and dams. Engineers use trigonometric functions to calculate angles, distances, heights, and slopes, which are critical for creating accurate blueprints and ensuring structural integrity. When analyzing forces acting on a structure (like wind load, tension in cables, or weight distribution), these forces are often resolved into their horizontal and vertical components using sine and cosine. This allows engineers to determine stresses and strains within structural members and ensure that the design can withstand the expected loads. For instance, calculating the slope of a roof or the forces in a truss system relies heavily on trigonometric principles.
Astronomy and Celestial Navigation
Historically, astronomy was one of the primary drivers for the development of trigonometry, and it remains a crucial tool in the field today. Astronomers use trigonometry to calculate the distances to nearby stars and planets, determine the positions of celestial objects, predict eclipses, and describe the orbits of planets. Techniques like parallax, which involves measuring the apparent shift in an object's position when viewed from two different points, rely heavily on trigonometric calculations to determine astronomical distances. Spherical trigonometry, which deals with triangles on the surface of a sphere, is particularly important for locating solar, lunar, and stellar positions. In celestial navigation, sailors and pilots have long used trigonometry with instruments like sextants to determine their position on Earth by measuring the angles of stars and the sun relative to the horizon. Modern satellite navigation systems, including GPS, also employ trigonometric principles for precise location tracking.
3D Graphics and Game Development
The vibrant and immersive worlds of 3D computer graphics and video games are built upon a foundation of trigonometric functions. Developers use trigonometry extensively to handle rotations, transformations, and perspectives in a 3D space. When a character moves, an object rotates, or the camera view changes, trigonometric calculations involving sine, cosine, and tangent are performed to update the positions and orientations of objects on the screen. For example, to rotate an object around a point, its coordinates are recalculated using sine and cosine functions of the rotation angle. Trigonometry is also used in lighting and shading models to determine how light interacts with surfaces, creating realistic visual effects. Pathfinding algorithms, character animations, and collision detection systems in games also frequently employ trigonometric principles to ensure smooth and believable interactions within the virtual environment.
Academic Pathways in Trigonometric Studies
Developing a strong understanding of trigonometric functions typically follows a structured educational path, starting from secondary education and progressing through higher academic levels. This journey equips learners with the foundational knowledge and advanced analytical skills necessary for various STEM fields.
High School Curriculum Integration
Trigonometry is a standard component of the high school mathematics curriculum, often introduced after algebra and geometry. Students typically begin by learning about the basic trigonometric ratios (sine, cosine, tangent) in the context of right-angled triangles. The curriculum then expands to include the unit circle definition of trigonometric functions, allowing for the analysis of angles beyond 90 degrees and negative angles. Key topics covered at this level usually include graphing trigonometric functions, understanding their periodic nature, amplitudes, and phase shifts, and solving basic trigonometric equations. An introduction to trigonometric identities, such as the Pythagorean identities, is also common. The goal is to provide students with a solid conceptual understanding and the ability to apply trigonometric principles to solve geometric problems and prepare them for more advanced mathematics courses like pre-calculus and calculus. For an overview of relevant topics in mathematics, you can browse Mathematics courses on OpenCourser.
This course is designed to help students deeply understand key high school math topics, including trigonometry, to build a strong foundation.
Undergraduate Courses in Calculus and Applied Mathematics
At the undergraduate level, particularly in mathematics, physics, and engineering programs, trigonometric functions are integral to many courses. Calculus courses heavily rely on and further develop concepts related to trigonometric functions. Students learn about the derivatives and integrals of trigonometric functions, their power series expansions (like Taylor series), and their applications in solving problems involving rates of change, optimization, and areas under curves. Inverse trigonometric functions and their derivatives are also explored in detail. In applied mathematics courses, trigonometric functions appear in the study of differential equations, linear algebra (e.g., rotations), complex analysis (through Euler's formula), and numerical methods. These courses demonstrate the power of trigonometry in modeling and solving complex problems across various scientific and engineering disciplines. Students also learn about Algebra as a prerequisite for these more advanced topics.
These courses are excellent for students looking to build on their pre-university mathematics knowledge, particularly focusing on functions and calculus where trigonometry is essential.
For further reading, these books cover calculus and precalculus topics where trigonometric functions play a crucial role.
Research Opportunities in Fourier Analysis or Differential Equations
For those pursuing advanced studies and research, trigonometric functions open doors to specialized areas of mathematics and its applications. Fourier analysis, which uses sine and cosine functions to represent and analyze complex periodic signals and functions, is a vast research field with applications in signal processing, image analysis, quantum mechanics, and solving partial differential equations. Researchers might explore new algorithms for Fourier transforms, their applications in data compression, or their use in understanding complex systems. Differential equations, which describe how quantities change, often have solutions involving trigonometric functions, especially when modeling oscillatory or wave phenomena. Research in this area can involve finding new methods to solve types of differential equations, analyzing the stability and behavior of their solutions, or applying them to model novel physical, biological, or engineering systems. Other advanced areas include harmonic analysis, wavelet theory, and the study of special functions, all ofwhich build upon or relate to trigonometric concepts.
Online Learning and Self-Study Strategies
The digital age has revolutionized access to education, and learning trigonometric functions is no exception. A wealth of online resources and tools are available for self-directed learners, students seeking supplementary material, and professionals looking to refresh or expand their mathematical skills. OpenCourser is an excellent platform to begin your search, offering a vast catalog of online courses from various providers, making it easier to find resources tailored to your learning style and goals.
Online courses offer several advantages. They often provide flexible schedules, allowing learners to study at their own pace. Many courses incorporate interactive elements, such as video lectures, quizzes, and assignments with immediate feedback, which can enhance understanding and retention. Platforms like OpenCourser allow you to save courses to a list, compare syllabi, and read reviews, helping you choose the most suitable options. For those on a budget, checking for deals on courses can also be beneficial.
Interactive Platforms for Visualizing Functions
Understanding the graphical nature of trigonometric functions is crucial, and interactive platforms excel in this area. Many websites and software applications offer dynamic graphing calculators where users can input trigonometric functions, adjust parameters (like amplitude, period, and phase shift), and instantly see how the graph changes. This hands-on approach helps solidify the connection between the algebraic form of a function and its visual representation. Some platforms also provide interactive unit circle diagrams, allowing learners to explore how sine, cosine, and tangent values change as an angle rotates around the circle. These visual tools can make abstract concepts more intuitive and engaging, significantly aiding the learning process. These visual explorations are particularly helpful for grasping concepts like periodicity and transformations of graphs.
The following courses emphasize the graphical representation and exploration of trigonometric functions, often using tools like Python, which can be highly interactive.
MOOC Courses for Applied Engineering Mathematics
Massive Open Online Courses (MOOCs) offered by universities and educational institutions worldwide provide comprehensive learning experiences in mathematics, including courses specifically focused on or heavily featuring trigonometry within the context of applied engineering mathematics. These courses often go beyond theoretical concepts and demonstrate how trigonometric functions are used to solve practical engineering problems. They might include modules on vector analysis, mechanics, circuit theory, or signal processing, all of which rely heavily on trigonometric principles. MOOCs frequently feature video lectures from experienced professors, graded assignments, and sometimes even projects that allow learners to apply their knowledge. Many MOOC platforms also have discussion forums where students can interact with peers and instructors, fostering a collaborative learning environment. For professionals, these courses can be a valuable way to upskill or refresh knowledge relevant to their field.
OpenCourser's Engineering category lists numerous courses that can help learners find relevant MOOCs and other online learning opportunities in applied mathematics for engineering.
Open-Source Tools for Computational Trigonometry
For learners interested in the computational aspects of trigonometry and its applications, numerous open-source tools are available. Programming languages like Python, with libraries such as NumPy and Matplotlib, provide powerful capabilities for performing trigonometric calculations, plotting functions, and simulating systems that involve trigonometry. [95nw74, ljy2je, n3wz71] GNU Octave or Scilab are open-source alternatives to MATLAB, offering environments for numerical computation and visualization. Computer Algebra Systems (CAS) like Maxima or SageMath can perform symbolic trigonometric manipulations, simplify expressions, and solve equations. Using these tools can provide a deeper understanding of how trigonometric functions behave and how they are implemented in software that solves real-world problems. Many online tutorials and communities support learning these tools, making them accessible for self-study. Projects involving these tools, such as creating a program to simulate wave interference or to model the motion of a simple pendulum, can be excellent ways to reinforce learning.
Exploring topics like Algebra and Mathematics in general on OpenCourser can lead to discovering courses that utilize such open-source tools for practical exercises.
Career Opportunities in Trigonometry-Driven Fields
A strong foundation in trigonometric functions and their applications opens doors to a wide array of rewarding and often high-demand career paths, particularly within Science, Technology, Engineering, and Mathematics (STEM) fields. While "Trigonometry Specialist" isn't typically a standalone job title, the principles of trigonometry are fundamental to the daily work of professionals in many sectors.
Roles in Aerospace Engineering and Robotics
Aerospace engineers rely heavily on trigonometry for designing and analyzing aircraft, spacecraft, and missiles. Calculations involving trajectories, orbital mechanics, navigation, and aerodynamics all require a deep understanding of trigonometric functions. For instance, determining the optimal launch angles, flight paths, and the forces acting on a vehicle in flight involves complex trigonometric computations. Similarly, the field of robotics is deeply intertwined with trigonometry. Engineers use trigonometric functions to define the movement and orientation of robotic arms, calculate joint angles for precise tasks, enable navigation in autonomous robots (including those used in extraterrestrial environments), and process sensor data for perception and control. Kinematics and dynamics of robotic systems are described using equations rich in trigonometric terms.
To explore careers in engineering further, you might consider looking into the broader Engineering field on OpenCourser.
Quantitative Analysis in Finance
While not immediately obvious, trigonometric functions, particularly in the context of Fourier analysis and signal processing techniques, find applications in quantitative finance. Financial analysts, or "quants," develop mathematical models to predict market movements, price derivatives, and manage risk. Some advanced models may use techniques derived from signal processing, which inherently involve trigonometric functions, to identify cyclical patterns or periodicities in financial data. While other mathematical areas like calculus, statistics, and probability are more central, a strong mathematical toolkit that includes an understanding of periodic functions and their analysis can be beneficial in certain specialized roles within the financial industry, particularly in algorithmic trading and financial modeling.
Geospatial Technology and GIS Specialists
Geospatial technology, including Geographic Information Systems (GIS), surveying, and cartography (map-making), fundamentally relies on trigonometric principles. Surveyors use trigonometry to measure angles and distances to determine the precise locations of points on the Earth's surface, create property boundaries, and support construction projects. GIS specialists use these foundational measurements and trigonometric calculations to create maps, analyze spatial data, and model geographic phenomena. Applications range from urban planning and environmental management to resource exploration and disaster response. The calculations involved in projecting the curved surface of the Earth onto a flat map also involve sophisticated trigonometry. Modern tools like GPS rely on trigonometric calculations based on signals from multiple satellites to pinpoint locations with high accuracy.
Acoustic Engineering Careers
Acoustic engineers, who deal with the science and engineering of sound and vibration, extensively use trigonometric functions. Sound travels in waves, and these waves are often modeled using sine and cosine functions. Acoustic engineers apply these principles in various areas, such as designing concert halls for optimal sound quality, reducing noise pollution from machinery or transportation, developing audio equipment like microphones and loudspeakers, and in medical applications like ultrasound imaging. Understanding wave interference, reflection, and diffraction—all of which are analyzed using trigonometry—is crucial for their work. Fourier analysis is also a key tool for decomposing complex sounds into their constituent frequencies, allowing for detailed sound analysis and manipulation.
Challenges in Mastering Trigonometric Functions
While trigonometric functions are powerful and widely applicable, students often encounter challenges in mastering them. These difficulties can stem from the abstract nature of the concepts, the shift in thinking from algebraic manipulation to geometric reasoning, and the memorization often associated with identities and specific angle values. However, with targeted strategies and a focus on conceptual understanding, these hurdles can be overcome.
Common Misconceptions About Angular Relationships
One common hurdle is developing an intuitive grasp of angular relationships and how they translate to trigonometric ratios. Students might initially struggle with the concept of radians versus degrees, or how angles greater than 90 degrees or negative angles are defined using the unit circle. The idea that sine, cosine, and tangent are ratios, and not absolute lengths, can also be a point of confusion. Misinterpreting the signs (+ or -) of trigonometric functions in different quadrants of the unit circle is another frequent issue. For example, understanding why cosine is positive in the first and fourth quadrants but negative in the second and third requires a solid mental model of the unit circle and the definitions of the functions based on x and y coordinates. Another misconception can arise with inverse trigonometric functions, where students might confuse sin-1(x) with 1/sin(x). Clarifying that inverse functions yield angles, while reciprocal functions yield ratios, is essential.
Bridging Abstract Concepts to Real-World Applications
For many learners, mathematics becomes more engaging and understandable when they can see its relevance to the real world. Trigonometry, with its deep roots in solving practical problems like surveying and astronomy, has many such connections, but these are not always immediately apparent from textbook exercises. Educators and self-learners can benefit from actively seeking out and exploring these applications. For example, understanding how architects use trigonometry to ensure the stability of structures, how game developers use it for 3D rotations, or how navigators use it to chart courses can make the abstract functions feel more tangible and purposeful. Projects that involve measuring real-world objects and applying trigonometric principles (e.g., calculating the height of a tree using its shadow and the angle of elevation of the sun) can be particularly effective in bridging this gap.
Courses that explicitly connect mathematical concepts to engineering or physics applications can be very helpful in this regard.
This book helps in understanding the practical side of trigonometry.
Addressing Computational vs. Conceptual Understanding Gaps
There can sometimes be a disconnect between being able to perform trigonometric calculations (e.g., finding the sine of an angle using a calculator or applying a formula) and truly understanding the underlying concepts. Rote memorization of formulas and identities without grasping their derivations or geometric interpretations can lead to a superficial understanding that falters when faced with novel problems. For instance, a student might be able to use the sum and difference formulas but not understand how they relate to rotations or geometric transformations. A balanced approach is key. While computational fluency is important, it should be built upon a strong conceptual foundation. This involves understanding why identities are true (perhaps through geometric proofs or unit circle derivations), visualizing the behavior of trigonometric graphs, and being able to explain the meaning of the functions rather than just manipulating their symbols. Emphasizing problem-solving that requires reasoning and interpretation, rather than just formulaic application, can help bridge this gap.
For students who find certain mathematical concepts challenging, resources like the OpenCourser Learner's Guide offer strategies for effective self-learning and overcoming common hurdles.
Advanced Topics in Trigonometric Analysis
Beyond the foundational concepts, trigonometric functions serve as building blocks for more advanced areas of mathematical analysis. These topics often involve integrating trigonometry with other branches of mathematics, such as calculus and complex analysis, to solve sophisticated problems and model complex phenomena in science and engineering.
Fourier and Laplace Transforms
Fourier transforms, and the related Fourier series, are powerful mathematical tools that decompose functions or signals into a spectrum of constituent frequencies, primarily using sine and cosine functions. This technique is fundamental in signal processing, image analysis, solving partial differential equations, and quantum mechanics. It allows engineers and scientists to analyze the frequency content of a signal, filter out unwanted noise, or compress data. The Laplace transform is another integral transform that is widely used in engineering and physics, particularly for solving linear ordinary and partial differential equations. It transforms a function of a real variable (often time) to a function of a complex variable (frequency). While not exclusively trigonometric, the solution and analysis of systems using Laplace transforms often involve or lead back to trigonometric functions when dealing with oscillatory or periodic behaviors.
These courses provide an introduction to these advanced transform techniques, where trigonometric functions are indispensable.
Applications in Quantum Mechanics
Trigonometric functions play a surprisingly significant role in the mathematical formalism of quantum mechanics, the theory that describes the physical properties of nature at the scale of atoms and subatomic particles. Wave functions, which describe the state of a quantum system, are often represented as complex-valued functions that can involve sines and cosines, particularly when dealing with particles in potential wells or periodic systems. The wave-like nature of particles, a central concept in quantum mechanics, is naturally described using trigonometric functions. Furthermore, Fourier analysis is extensively used to switch between position and momentum representations of quantum states. The study of spin and angular momentum in quantum systems also involves mathematical structures that are closely related to rotations and, therefore, to trigonometry.
Topological Approaches to Periodic Functions
Topology, a branch of mathematics concerned with the properties of space that are preserved under continuous deformations, can offer abstract and powerful ways to understand periodic functions, including trigonometric ones. The study of functions on a circle (which is topologically equivalent to identifying the endpoints of an interval, representing periodicity) naturally involves concepts deeply related to trigonometric functions and Fourier series. For instance, the set of continuous periodic functions on an interval forms a vector space, and trigonometric functions (sines and cosines of different frequencies) can form a basis for this space under certain conditions. Advanced topics might involve studying the topological properties of spaces of periodic functions, or using topological methods to prove existence or properties of solutions to differential equations that exhibit periodic behavior. This area connects the analytical properties of trigonometric functions with more abstract geometric and topological structures.
For those looking to explore broader mathematical concepts, the Mathematics section on OpenCourser provides a gateway to various subfields.
Ethical Considerations in Trigonometric Applications
While mathematics itself, including trigonometry, is often viewed as an objective and neutral discipline, its applications can raise significant ethical questions. The power of mathematical modeling, which frequently employs trigonometric functions, to influence decisions and shape technologies means that mathematicians, scientists, and engineers have a responsibility to consider the societal impact of their work.
Surveillance Technology and Trigonometric Algorithms
Trigonometric functions are fundamental to many technologies used in surveillance. For example, algorithms for object tracking, facial recognition, and determining the location of individuals (e.g., via triangulation of signals) often rely on geometric calculations that involve trigonometry. While these technologies can have beneficial uses, such as in security or search and rescue, they also pose risks to privacy and can be used for mass surveillance or to unfairly target individuals or groups. The precision with which locations can be determined or movements tracked, enabled by trigonometric calculations, raises questions about the balance between security and individual liberties. Ethical considerations include who has access to this data, how it is used, and the potential for misuse or algorithmic bias that could lead to discriminatory outcomes. The Brookings Institution has explored the complexities of AI surveillance, an area where such algorithms are prevalent.
Bias in AI Systems Using Trigonometric Pattern Recognition
Artificial intelligence (AI) systems, particularly those involved in pattern recognition (like image analysis or voice recognition), may use underlying algorithms that incorporate trigonometric concepts, especially when dealing with geometric features, rotations, or signal processing. If the data used to train these AI systems is biased, or if the algorithms themselves inadvertently encode biases, the outcomes can be discriminatory. For example, a facial recognition system might perform less accurately for certain demographic groups if it was primarily trained on data from other groups. While trigonometry itself isn't biased, its application within complex algorithms that make decisions affecting people's lives (e.g., in hiring, loan applications, or criminal justice) necessitates careful scrutiny for fairness and equity. The mathematical models, including those using trigonometric components, must be designed and evaluated with an awareness of potential biases to avoid perpetuating or amplifying societal inequalities. Integrating ethical principles into the mathematical modeling of algorithms is crucial to prevent manipulation and ensure fairness.
Environmental Impact of Trigonometric Modeling in Climate Science
Trigonometric functions are essential in modeling complex environmental systems, including climate science. Models that predict weather patterns, sea-level rise, the spread of pollutants, or the impact of deforestation often use trigonometric relationships to describe cyclical phenomena (like seasons), wave motions (like ocean currents), or spatial distributions. The accuracy and interpretation of these models have significant ethical implications, as they inform policy decisions that can have profound and long-lasting environmental and societal consequences. For instance, predictions about climate change can influence energy policy, infrastructure investment, and international agreements. Modelers have an ethical responsibility to be transparent about the assumptions, uncertainties, and limitations of their models. Gaps in the transparency of computational models or miscommunication of their results can lead to public mistrust or flawed policy decisions. Ensuring that these powerful tools are used responsibly requires careful consideration of their potential impacts and a commitment to clear communication of their findings to policymakers and the public. As discussed by the National Academy of Engineering, modeling carries important ethical implications, especially when models are not transparent.
Frequently Asked Questions (Career Focus)
Navigating a career path that utilizes mathematical skills, including a strong understanding of trigonometric functions, often brings up practical questions about specific roles, industry transitions, and the evolving job market. Here are some common inquiries addressed for career advisors and industry professionals.
Essential trigonometry skills for robotics engineers?
Robotics engineers need a robust understanding of trigonometry for several key tasks. Essential skills include:
- Kinematics and Inverse Kinematics: Calculating the position, orientation, velocity, and acceleration of robot arms and mobile robots using joint angles (forward kinematics) and determining the required joint angles to reach a desired position and orientation (inverse kinematics). This heavily involves sine, cosine, and tangent functions, as well as their inverses.
- Transformations: Using rotation matrices (which are built from trigonometric functions) to represent and manipulate the orientation of objects and coordinate frames in 3D space.
- Navigation and Path Planning: For mobile robots, calculating paths, steering angles, and understanding sensor data (e.g., from Lidar or cameras) often involves trigonometric calculations to determine distances, angles, and relative positions.
- Sensor Data Interpretation: Many sensors provide data that needs to be interpreted geometrically, often requiring trigonometry to convert raw sensor readings into meaningful spatial information.
- Control Systems: Designing controllers for robot movements often involves trigonometric components, especially for rotational motion.
A solid grasp of 2D and 3D coordinate systems and vector mathematics, which are intertwined with trigonometry, is also crucial.
This course delves into the practical application of mathematics in robotics.
record:22093f
Can trigonometry specialists transition to fintech?
While "trigonometry specialist" is not a common job title, individuals with strong mathematical skills, including a deep understanding of trigonometry and its applications in areas like signal processing or data analysis (e.g., through Fourier analysis), can potentially transition into certain roles in the financial technology (fintech) sector. Fintech companies often seek quantitative analysts ("quants"), data scientists, and software developers with strong analytical and problem-solving abilities. Trigonometry-related skills might be applicable in:
- Algorithmic Trading: Some advanced trading algorithms might use signal processing techniques (which rely on trigonometric functions via Fourier analysis) to identify patterns or cycles in market data.
- Financial Modeling: While calculus, statistics, and probability are more central, complex models might occasionally involve periodic functions or geometric considerations where trigonometric understanding is beneficial.
- Data Analysis: Skills in analyzing complex data sets, which can be honed through advanced mathematical studies involving trigonometry, are highly valued.
However, a direct transition based solely on trigonometry expertise is less likely than one based on broader quantitative skills. Professionals looking to make this switch would typically need to supplement their mathematical background with knowledge of finance, programming (e.g., Python, R, C++), statistics, machine learning, and financial market dynamics. Online courses in these areas, such as those found on OpenCourser's Finance & Economics section, can be very helpful for building the necessary domain knowledge.
Impact of AI on traditional trigonometry careers?
Artificial Intelligence (AI) is transforming many fields, including those that traditionally rely on mathematical skills like trigonometry. The impact is nuanced:
- Automation of Routine Calculations: AI and advanced software can automate many of the routine calculations that previously required manual application of trigonometric formulas. This means that the demand for performing such calculations by hand is decreasing.
- Enhanced Tools: AI can provide more powerful tools for engineers, designers, and scientists, allowing them to tackle more complex problems where trigonometric principles are embedded within sophisticated software. For example, CAD software or simulation tools may perform complex trigonometric calculations seamlessly in the background.
- Shift in Skill Demand: The emphasis is shifting from manual calculation to understanding the underlying principles, interpreting results generated by AI tools, and applying mathematical reasoning to solve complex problems. There's a greater need for individuals who can develop, validate, and critically evaluate the models and algorithms that AI systems use, many of which are built on mathematical foundations including trigonometry.
- New Opportunities: AI is also creating new roles. For instance, developing AI algorithms for robotics, computer vision, or signal processing often requires a deep understanding of mathematics, including trigonometry.
So, while AI might reduce the need for some traditional manual tasks, it also elevates the importance of a strong conceptual understanding of mathematics and creates new opportunities for those who can work with and develop AI-driven systems. The World Economic Forum has published reports on the Future of Jobs, which often touches on the impact of AI and automation across various sectors.
Global demand for trigonometric modeling experts?
The demand isn't typically for "trigonometric modeling experts" per se, but rather for professionals in fields like engineering (aerospace, mechanical, civil, electrical), physics, computer science (especially graphics, game development, robotics), data science, and surveying who possess strong mathematical modeling skills, where trigonometry is a fundamental component. The global demand for these STEM professionals is generally robust and projected to grow, according to data from sources like the U.S. Bureau of Labor Statistics on math occupations and engineering fields. As technology advances, the need for individuals who can apply mathematical principles to solve complex problems remains high. Fields like renewable energy, autonomous systems, advanced manufacturing, and space exploration are creating new opportunities where these skills are vital. The demand is often for individuals who can combine trigonometric understanding with other mathematical disciplines (calculus, linear algebra, differential equations, statistics) and apply them using computational tools.
Entry-level roles requiring trigonometric proficiency?
Many entry-level STEM roles require a working knowledge of trigonometry as part of a broader mathematical skillset. Examples include:
- Junior Engineer (various disciplines): Assisting with design, analysis, and testing, which often involves geometric calculations, force analysis, or signal processing.
- CAD Drafter/Technician: Creating technical drawings and plans, where understanding angles, dimensions, and geometric relationships is crucial.
- Surveying Technician: Assisting land surveyors with field measurements and data processing.
- Game Development Intern/Junior Programmer: Working on aspects of game physics, character animation, or 3D rendering.
- Robotics Technician/Junior Robotics Engineer: Assisting in the assembly, testing, and programming of robotic systems.
- Lab Technician (Physics/Engineering): Setting up experiments and analyzing data that may involve wave phenomena or geometric measurements.
These roles typically require at least a bachelor's degree in a relevant STEM field, where trigonometry is a foundational part of the curriculum. Proficiency is often demonstrated through coursework and projects rather than a specific "trigonometry test" in job applications, although technical interviews might include problem-solving that draws on these concepts.
Continuing education paths for professionals?
Professionals in fields utilizing trigonometry can pursue several continuing education paths to deepen their expertise, stay current with new technologies, or pivot to related areas:
- Advanced Degrees: Master's or Ph.D. programs in engineering, physics, applied mathematics, computer science, or data science can provide specialized knowledge and research opportunities.
- Online Courses and Certifications: Platforms like OpenCourser list numerous courses on advanced topics such as digital signal processing, machine learning, robotics, computational geometry, finite element analysis, or specialized software (e.g., advanced CAD, simulation tools). [For instance, browsing Computer Science courses or Data Science courses can reveal relevant options.]
- Professional Workshops and Seminars: Industry conferences and professional organizations often offer workshops on new tools, techniques, and research in specialized fields.
- Cross-Disciplinary Learning: Professionals might benefit from learning more about related fields. For example, an engineer might take courses in data science or AI to understand how these can be applied in their domain.
- Learning New Programming Languages/Software: Staying proficient with industry-standard software and learning new programming languages relevant to their field (e.g., Python for data analysis and machine learning, C++ for high-performance computing) is crucial.
Lifelong learning is key in rapidly evolving technological fields. Focusing on areas where mathematical modeling and computational skills are in high demand can enhance career prospects.
Understanding trigonometric functions is more than an academic exercise; it's a gateway to comprehending and shaping the world. From the grandeur of celestial mechanics to the intricacies of digital technology and engineering marvels, these mathematical tools are fundamental. While the path to mastering them can have its challenges, the journey is rewarding, opening up diverse and exciting career opportunities. For those willing to explore their depths, trigonometric functions offer a powerful lens through which to view and interact with the complexities of our universe.